城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度,请返回 由这些建筑物形成的 天际线 。
每个建筑物的几何信息由数组 buildings 表示,其中三元组 buildings[i] = [lefti, righti, heighti] 表示:
lefti是第i座建筑物左边缘的x坐标。righti是第i座建筑物右边缘的x坐标。heighti是第i座建筑物的高度。
你可以假设所有的建筑都是完美的长方形,在高度为 0 的绝对平坦的表面上。
天际线 应该表示为由 “关键点” 组成的列表,格式 [[x1,y1],[x2,y2],...] ,并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点,y 坐标始终为 0 ,仅用于标记天际线的终点。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
注意:输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案;三条高度为 5 的线应该在最终输出中合并为一个:[...[2 3], [4 5], [12 7], ...]
示例 1:
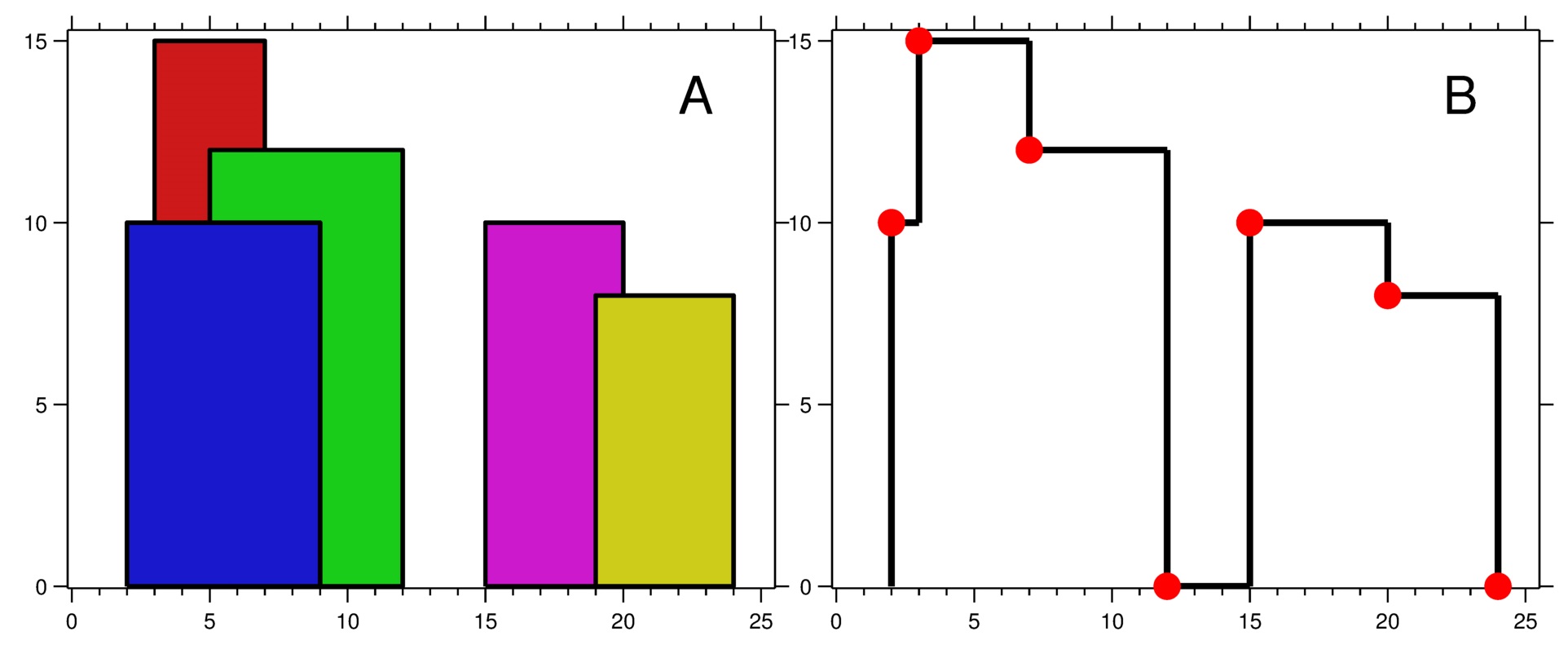
输入:buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]] 输出:[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]] 解释: 图 A 显示输入的所有建筑物的位置和高度, 图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。
示例 2:
输入:buildings = [[0,2,3],[2,5,3]] 输出:[[0,3],[5,0]]
提示:
1 <= buildings.length <= 104
0 <= lefti < righti <= 231 - 1
1 <= heighti <= 231 - 1
buildings 按 lefti 非递减排序
一.扫描线
扫描线算法多用于解决图像问题。是通过虚构一条线(多是与坐标轴平行),用来沿着垂直于此线的方向扫描获取当前图像信息解决问题。
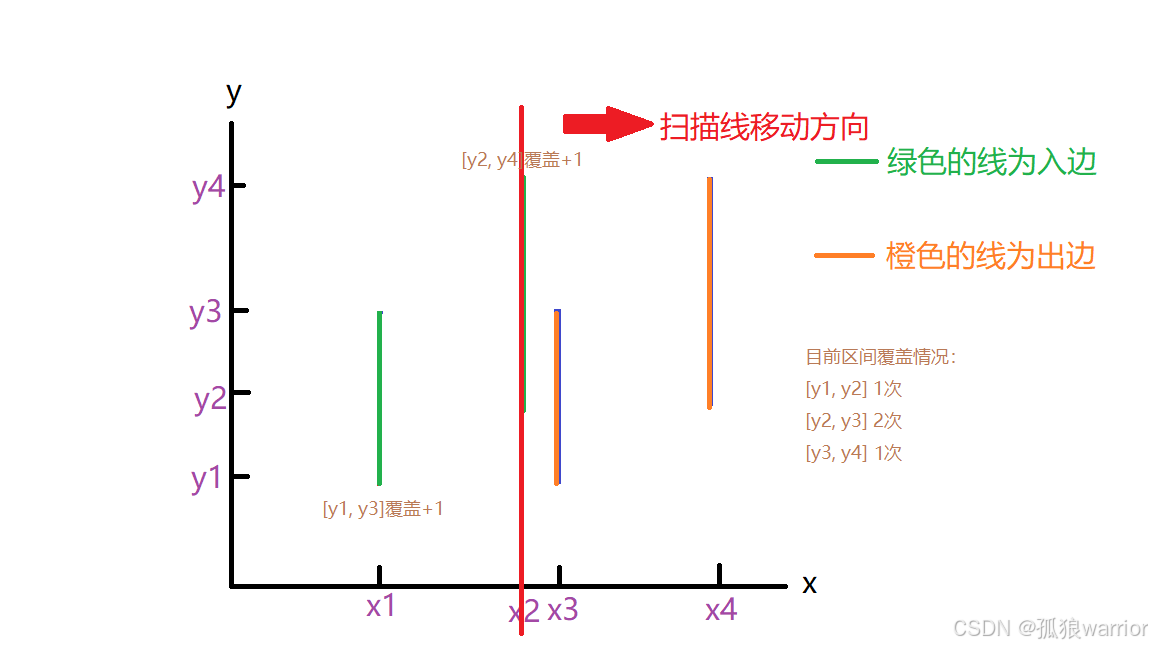
核心是(以y轴方向的扫描线为准)将所有图形的横坐标以从小到大的顺序排列,以一个个相邻的横坐标为一个个的隔间,获取这些隔间的纵坐标或其他信息解决问题。
此题中运用扫描线算法,可以通过这一个个隔间的高度变化来获取坐标。具体情况,我们可以自己在纸上画出不同的情况,来挖掘其中的规律。
class Solution {
public List<List<Integer>> getSkyline(int[][] buildings) {
//优先队列寻找当前最高高度
PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> b[1] - a[1]);
//记录一个个图形的x左右坐标
List<Integer> boundaries = new ArrayList<Integer>();
for (int[] building : buildings) {
boundaries.add(building[0]);
boundaries.add(building[1]);
}
Collections.sort(boundaries);
List<List<Integer>> res = new ArrayList<List<Integer>>();
int n = buildings.length, idx = 0;
for (int boundary : boundaries) {
while (idx < n && buildings[idx][0] <= boundary) {//添加当前区间的各个高度(左横坐标为准)
pq.offer(new int[]{buildings[idx][1], buildings[idx][2]});
idx++;
}
while (!pq.isEmpty() && pq.peek()[0] <= boundary) {//当前高度是否超过当前间隔
pq.poll();
}
int maxn = pq.isEmpty() ? 0 : pq.peek()[1];
if (res.size() == 0 || maxn != res.get(res.size() - 1).get(1)) {//让第一次能添加以及去除掉同等高度的间隔
res.add(Arrays.asList(boundary, maxn));
}
}
return res;
}
}二.线段树
线段树是一种数据结构,是一种二叉树,将目标数组分成一个一个的小区间(即最底层没有子叶的节点),并对这些小区间进行赋值,从而可以高效的对这些小区间进行操作。

线段树这个数据结构经常搭配其他的算法,通过这些其他的算法对小区间进行操作,再把值返回管理小区间的节点,这么一层层下来最终得到根节点(即答案)。
此题中,我们可以将一个个图形的坐标作为值存在无子叶节点中,通过我们对这些坐标规律的观察写成的算法实现一层层上层分支的构建,最终得到答案。
class Solution {
//x轴为线段树的边界 结点值代表这段x轴内的最高高度
//遍历每个建筑的左上点和右下点 如果其是这个区间最高点 就加入答案
class Node {
Node left, right;
long val, add;
}
private int N;//线段树范围
private Node root = new Node();
public List<List<Integer>> getSkyline(int[][] buildings) {
int n = buildings.length;
N = 1;
for (int i = 0; i < n; i++) {
N = Math.max(N, buildings[i][1]);// 找出线段树的范围
}
Arrays.sort(buildings, (o1,o2) -> o1[2]-o2[2]);//按高度从小到大排序
List<Integer> points = new ArrayList<>();
for (int[] building : buildings) {
int l = building[0],r=building[1],h=building[2];
points.add(l);
points.add(r);
update(root,0,N,l,r-1,h);//右边界的高度不算防止端点覆盖(r-1)
}
Collections.sort(points);//对坐标点排序,按照从左至右的顺序可以打印出最终结果
points = points.stream().distinct().collect(Collectors.toList());//去除重复坐标点
List<List<Integer>> ans = new ArrayList<>();
for (int i = 1; i < points.size(); i++) {//已经对已经对横坐标与高度从小到大排序,所以只需要一个接一个按数组顺序查询即可
int height=(int)query(root,0,N,points.get(i-1),points.get(i)-1);
int j=i+1;
while (j<points.size() && query(root,0,N,points.get(j-1),points.get(j)-1)==height) j++;//跳过相同高度
ans.add(Arrays.asList(points.get(i-1),height));
i = j-1;
}
ans.add(Arrays.asList(points.get(points.size()-1),0));//最后一个点坐标单独添加
return ans;
}
public void update(Node node, long start, long end, long l, long r, long val) {
if (l <= start && end <= r) {
node.val = val;
node.add = val;
return;
}
long mid = (start + end) >> 1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
}
public long query(Node node, long start, long end, long l, long r) {
if (l <= start && end <= r) return node.val;
long mid = (start + end) >> 1, ans = 0;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) ans = query(node.left, start, mid, l, r);
if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
return ans;
}
// 推懒惰标记的函数(延迟更新,只在要用的时候对后续的枝叶更新)
private void pushDown(Node node, long leftNum, long rightNum) {
//开枝散叶
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return;
//因为是按照高度从小到大的顺序查询,所以第二次查到相同的非底层叶子节点会更新为更大的高度(即更新val)
node.left.val = node.add;
node.right.val = node.add;
node.left.add = node.add;
node.right.add = node.add;
node.add = 0;
}
}三.分治
分治是一种方法,即分而治之。分治与线段树有些类似,都是将原本的问题分成一个个的小段解决问题。通过最简单的两两比对,再对这些得出的结果继续两两比对层层递进得出最终答案。
此题中,不管是采取什么样的顺序比对,都不会影响最终图形的天际线,所以我们可以采取分治的思想解题。
import java.util.*;
class Solution {
// 分治法
public List<List<Integer>> getSkyline(int[][] buildings) {
return segment(buildings, 0, buildings.length-1);
}
private List<List<Integer>> segment(int[][] buildings, int l, int r) {
List<List<Integer>> ans = new ArrayList<>();
if (l == r) {
ans.add(Arrays.asList(buildings[l][0], buildings[l][2]));
ans.add(Arrays.asList(buildings[l][1], 0));
return ans;
}
int mid = l + (r - l) / 2;
List<List<Integer>> left = segment(buildings, l, mid);
List<List<Integer>> right = segment(buildings, mid + 1, r);
int m = 0, n = 0;
int lpreH = 0, rpreH = 0;
int leftX, leftY, rightX, rightY;
while (m < left.size() || n < right.size()) {
// 当有一边完全加入到res时,则加入剩余的那部分
if (m >= left.size())
ans.add(right.get(n++));
else if (n >= right.size())
ans.add(left.get(m++));
else {
leftX = left.get(m).get(0);
leftY = left.get(m).get(1);
rightX = right.get(n).get(0);
rightY = right.get(n).get(1);
if (leftX < rightX) {
if (leftY > rpreH) ans.add(left.get(m));
else if (lpreH > rpreH) ans.add(Arrays.asList(leftX, rpreH));
lpreH = leftY;
m++;
} else if (leftX > rightX) {
if (rightY > lpreH) ans.add(right.get(n));
else if (rpreH > lpreH) ans.add(Arrays.asList(rightX, lpreH));
rpreH = rightY;
n++;
} else {
if (leftY >= rightY && leftY != (lpreH > rpreH ? lpreH : rpreH)) ans.add(left.get(m));
else if (leftY <= rightY && rightY != (lpreH > rpreH ? lpreH : rpreH)) ans.add(right.get(n));
lpreH = leftY;
rpreH = rightY;
m++;
n++;
}
}
}
return ans;
}
}最终,如果想不清这一个个矩形与答案坐标的关系,就看看这个图吧:
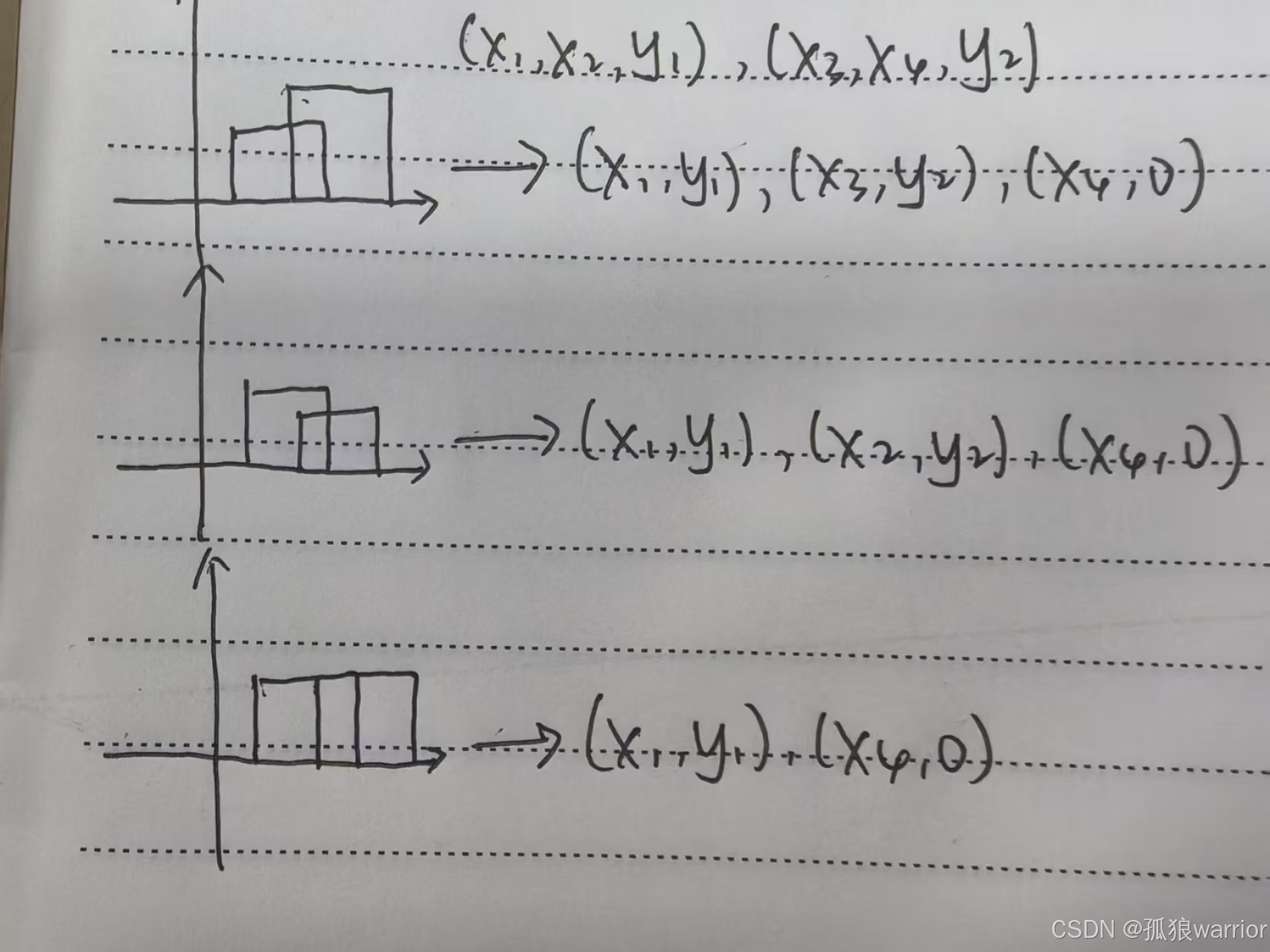























 1499
1499

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








