一、从零搭建神经网络
1、利用numpy来搭建网络模型
import numpy as np
import torch
"""
热身: 用numpy实现两层神经网络
一个全连接ReLU神经网络,一个隐藏层,没有bias。用来从x预测y,使用L2 Loss。
这一实现完全使用numpy来计算前向神经网络,loss,和反向传播。
numpy ndarray是一个普通的n维array。它不知道任何关于深度学习或者梯度(gradient)的知识,也不知道计算图(computation graph),只是一种用来计算数学运算的数据结构。
"""
def numpyNet():
N = 64 # batch_size大小
D_in = 1000 # 输入的维度
H = 100 # 隐藏的维度
D_out = 10 # 输出的维度
x = np.random.randn(N,D_in) # 创建随机的输入矩阵
y = np.random.randn(N,D_out) # 创建随机的输出矩阵
# 随机初始化权重值
w1 = np.random.randn(D_in,H)
w2 = np.random.randn(H,D_out)
learning_rate = 1e-6
for t in range(500):
# 前向传递,计算预测值y
h = x.dot(w1)
h_relu = np.maximum(h,0) # relu激活函数:小于0的元素设置为0
y_pre = h_relu.dot(w2)
# 计算和打印损失
loss = np.square(y_pre - y).sum()
print(t,loss)
# 计算y_pre的梯度
grad_y_pre = 2.0 * (y_pre - y)
grad_w2 = h_relu.T.dot(grad_y_pre)
grad_h_relu = grad_y_pre.dot(w2.T)
grad_h = grad_h_relu.copy()
grad_h[h<0] = 0
grad_w1 = x.T.dot(grad_h)
# 更新权重
w1 -= learning_rate*grad_w1
w2 -= learning_rate*grad_w2
2、使用tensor来搭建网络模型
def tensorNet():
N = 64 # batch_size大小
D_in = 1000 # 输入的维度
H = 100 # 隐藏的维度
D_out = 10 # 输出的维度
x = torch.randn(N, D_in,dtype=torch.float) # 创建随机的输入矩阵
y = torch.randn(N, D_out,dtype=torch.float) # 创建随机的输出矩阵
# 随机初始化权重值
w1 = torch.randn(D_in, H, dtype=torch.float,requires_grad=True)
w2 = torch.randn(H, D_out, dtype=torch.float,requires_grad=True)
learning_rate = 1e-6
for t in range(500):
# 前向传递,计算预测值y
h = x.mm(w1)
h_relu = h.clamp(min=0) # 将每个元素压缩到[min,max]之间
y_pre = h_relu.mm(w2)
# 计算和打印损失
loss = (y_pre - y).pow(2).sum()
print(t, loss.item()) # 当矩阵中只有一个元素时,使用item()返回矩阵中的数
# 计算y_pre的梯度
loss.backward()
# 更新权重
with torch.no_grad():
w1 -= learning_rate * w1.grad
w2 -= learning_rate * w2.grad
# 更新权重后需要对权重的梯度清零
w1.grad.zero_()
w2.grad.zero_()
3、利用torch框架来搭建模型
def nnNet():
N = 64 # batch_size大小
D_in = 1000 # 输入的维度
H = 100 # 隐藏的维度
D_out = 10 # 输出的维度
x = torch.randn(N, D_in, dtype=torch.float) # 创建随机的输入矩阵
y = torch.randn(N, D_out, dtype=torch.float) # 创建随机的输出矩阵
model = torch.nn.Sequential(
torch.nn.Linear(D_in,H),
torch.nn.ReLU(),
torch.nn.Linear(H,D_out),
)
loss_fn = torch.nn.MSELoss(reduction='sum')
learning_rate = 1e-4
for t in range(500):
y_pre = model(x)
loss = loss_fn(y_pre,y)
print(t,loss.item())
model.zero_grad()
loss.backward()
with torch.no_grad():
for param in model.parameters():
param -= learning_rate * param.grad
4、继承 torch.nn.Model 来搭建网络
class myNet(torch.nn.Module):
def __init__(self, D_in, H, D_out):
super(myNet,self).__init__()
self.linear1 = torch.nn.Linear(D_in, H)
self.linear2 = torch.nn.Linear(H, D_out)
'''
在forward函数中,我们接受输入数据的张量,我们必须返回
输出数据的张量。我们可以使用构造函数中定义的模块作为
以及张量上的任意算符。
'''
def forward(self,x):
h_relu = self.linear1(x).clamp(min = 0)
y_pred = self.linear2(h_relu)
return y_pred
def modelNet():
N, D_in, H, D_out = 64, 1000, 100, 10
# Create random Tensors to hold inputs and outputs
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)
model = myNet(D_in,H,D_out)
print(model)
criterion = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(),lr = 1e-4)
for t in range(500):
y_pred = model(x)
loss = criterion(y_pred,y)
print(t,loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
二、数据集
1、从网络中获取MNIST数据集
import torch
import torchvision.transforms as transforms
import torchvision
from matplotlib import pyplot as plt
# root是数据集存放目录,获取训练集则train为true否则为false,获取的数据集是PIL类型,需要转化为张量
mnist_train = torchvision.datasets.FashionMNIST(root='./Datasets',train=True,download=True,transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='./Datasets',train=False,download=True,transform=transforms.ToTensor())
# 获取的数据是二维的,第一维是(1,28,28)Feature,第二维是label
# print(type(mnist_train))
# # print(len(mnist_train),len(mnist_test))
# 定义一个函数,将目标值转化为对应的图片标签
def get_fasionMNIST_label(labels):
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
return text_labels[labels]
# 定义一个函数,用来展示多个数据集图片及其标签值
# imgs是多个feature的集合,labels是目标值的集合
def showImage(imgs,lables):
fig,ax = plt.subplots(1,len(imgs),figsize=(12,12))
for a,img,label in zip(ax,imgs,lables):
a.imshow(img.view(28,28).numpy()) # feature是(1,28,28)的tensor,需要转化为相应numpy才能展示
a.set_title(label)
a.axes.get_xaxis().set_visible(False) # 关闭刻度
a.axes.get_yaxis().set_visible(False)
print(a)
plt.show()
def showImage2(imgs,labels):
fig = plt.figure(figsize=(12, 12))
for i,img,label in zip(range(len(imgs)),imgs,lables):
plt.subplot(1,len(imgs),i+1)
plt.imshow(img.view(28,28).numpy())
plt.title(label)
plt.xticks([])
plt.yticks([])
plt.show()
# 展示10个数据集结果
imgs,lables = [],[]
for i in range(10):
imgs.append(mnist_train[i][0])
lables.append(get_fasionMNIST_label(mnist_train[i][1]))
2、获取小批量数据集
# 获取小批量数据
batch_size = 256
if sys.platform.startswith("win"):
num_works = 0 # 0表示不用额外的进程加速读取数据
else:
num_works = 4
train_iter = torch.utils.data.DataLoader(mnist_train,batch_size=batch_size,shuffle=True,num_workers=num_works)
test_iter = torch.utils.data.DataLoader(mnist_test,batch_size=batch_size,shuffle=True,num_workers=num_works)
三、softmax回归的实现
使用softmax回归的原因: 在图像多分类等问题中,输出的预测结果常常是多维的,此时就需要将这些预测结果使用softmax回归压缩到(0,1)之间,选取概率最大的预测结果作为最终的分类结果。
1、gather()函数
tensor对象.gather()
def gather_example():
N, C = 4, 5
s = torch.randn(N, C)
y = torch.LongTensor([1, 2, 1, 3]) # 必须要为 LongTensor 不然会报错
print(s)
print(y)
# gether()作用:通过y列表的索引值,对每一行/列进行索引
print(s.gather(1,y.view(-1, 1)).squeeze()) # .squeeze()用来展成一维
'''
输出:
tensor([[-1.0408, 0.9166, -1.3042, -1.1097, 0.0299],
[-0.0498, 1.0651, 0.8860, -0.8110, 0.6737],
[-1.1233, -0.0919, 0.1405, 1.1191, 0.3152],
[ 1.7528, -0.7396, -1.2425, -0.1752, 0.6990]])
tensor([1, 2, 1, 3])
tensor([ 0.9166, 0.8860, -0.0919, -0.1752])
'''
torch.gather()
b = torch.Tensor([[1,2,3],[4,5,6]])
print (b)
index_1 = torch.LongTensor([[0,1],[2,0]])
index_2 = torch.LongTensor([[0,1,1],[0,0,0]])
print (torch.gather(b, dim=1, index=index_1)) # 按行来进行索引
print (torch.gather(b, dim=0, index=index_2)) # 按列来进行索引
'''
输出为:
1 2 3
4 5 6
[torch.FloatTensor of size 2x3]
1 2
6 4
[torch.FloatTensor of size 2x2]
1 5 6
1 2 3
[torch.FloatTensor of size 2x3]
'''
2、softmax的实现函数

其中:

def softmax(X):
X_exp = X.exp()
partion = X_exp.sum(dim=1,keepdim=True)
return X_exp/partion # 利用广播机制,逐列相除
3、定义一个单层softmax网络
def net(X):
return softmax(torch.mm(X.view(-1,num_input),w)+b)
4、交叉熵损失函数
4.1 交叉熵定义
作用:衡量两个概率分布差异,通常用来衡量softmax输出结果的预测值与目标值之间的概率分布差异

例如对于一组训练结果:

4.2 交叉熵损失函数

如果每个样本只有一个标签,那么交叉熵损失可以简写成:

代码实现:
y_pre = torch.tensor([[0.1,0.3,0.6],[0.3,0.2,0.5]])
y = torch.LongTensor([0, 2])
print(y_pre.gather(1,y.view(-1,1)))
'''
输出:
tensor([[0.1000],
[0.5000]])
'''
'''
在该例子中,真实值为一维label,利用label值作为索引选择对应预测值的概率,
再用公式-logYi计算某一预测值的损失函数。
'''
# 交叉熵损失函数实现
def cross_entropy(y_pre,y):
return -torch.log(y_pre.gather(1,y.view(-1,1)))
loss = cross_entropy(y_pre,y).sum()
# 利用pytorch自带交叉熵损失函数
# loss = torch.nn.CrossEntropyLoss()
5、定义精确率
5.1 单个训练样本的精确率
def accuracy(y_pre,y):
# y_pre.argmax(dim=1)表示指定维数最大元素的序号
# (y_pre.argmax(dim=1) == y)返回的是一个byteTensor的0/1矩阵
# 将上述矩阵转化为float类型的0/1矩阵,.mean()求0/1矩阵的均值即为准确率
# .item()取出矩阵中唯一的元素
return (y_pre.argmax(dim=1) == y).float().mean().item()
5.2 整个网络的精确率
def evaluate_accuracy(data_iter,net):
acc = 0.0
n = 0
for X,y in data_iter:
# 每次抛出batch_size个,一共抛出len/batch_size次
# data_iter大小为len/batch_size
# X.shape:(batch_size,28*28),y.shape:(batch_size,1)
print(X.shape,y.shape)
acc += (net(X).argmax(dim=1) == y).float().mean().item()
# print(net(X).shape) -->(10,10)
n += 1 # n为data_iter的大小,即len/batch_size
return acc/n
data_iter = torch.utils.data.DataLoader(mnist_test,batch_size=10,shuffle=True,num_workers=0)
print(evaluate_accuracy(data_iter,net)) # 由于是随机初始化的net,结果近似为1/类别数
6、定义一个SGD优化器
优化过程:

其中:B 为batch_size大小,μ 为学习率
def sgd(params,lr,batch_size):
for param in params:
param.data -= lr*param.grad / batch_size
7、softmax网络训练
def train(net,train_iter,test_iter,loss,num_epochs,batch_size,params=None,lr=None,optimizer=None):
for epoch in range(num_epochs):
train_l_sum,train_acc_sum,n = 0.0,0.0,0
for X,y in train_iter:
y_pre = net(X)
l = loss(y_pre,y).sum() # 交叉熵损失求和
# 梯度清零
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
sgd(params,lr,batch_size)
else:
optimizer.step()
train_l_sum += l.item() # 训练损失之和
train_acc_sum += (y_pre.argmax(dim=1) == y).float().sum().item() # 注意该处是求和而没有求平均
n += y.shape[0] # n表示所有的数据集个数
test_acc = evaluate_accuracy(test_iter,net)
print('epoch %d,loss %.4f,train acc %.3f,test acc %.3f'%(epoch+1,train_l_sum/n,train_acc_sum/n,test_acc))
# 传入参数开始训练
train(net,train_iter,test_iter,cross_entropy,5,batch_size,params=[w,b],lr=0.1)
'''
输出:
epoch 1,loss 0.7845,train acc 0.748,test acc 0.792
epoch 2,loss 0.5698,train acc 0.813,test acc 0.810
epoch 3,loss 0.5254,train acc 0.826,test acc 0.818
epoch 4,loss 0.5014,train acc 0.832,test acc 0.821
epoch 5,loss 0.4859,train acc 0.836,test acc 0.826
'''
8、利用pytorch框架简洁实现softmax网络
8.1 写法一
from collections import OrderedDict
class FlattenLayer(torch.nn.Module):
def __init__(self):
super(FlattenLayer,self).__init__()
def forward(self,x):
y = x.view(x.shape[0],-1)
return y
net2 = torch.nn.Sequential(
# FlattenLayer(),
# torch.nn.Linear(num_input,num_output)
OrderedDict([
("flatten",FlattenLayer()),
("linear",torch.nn.Linear(num_input,num_output))
])
)
# 定义优化器
optimizer = torch.optim.SGD(net2.parameters(),lr=0.1)
# 定义损失函数
loss = torch.nn.CrossEntropyLoss()
# 训练
train(net2,train_iter,test_iter,loss,5,batch_size,None,None,optimizer=optimizer)
'''
输出:
epoch 1,loss 0.0031,train acc 0.748,test acc 0.789
epoch 2,loss 0.0022,train acc 0.813,test acc 0.809
epoch 3,loss 0.0021,train acc 0.826,test acc 0.811
epoch 4,loss 0.0020,train acc 0.832,test acc 0.819
epoch 5,loss 0.0019,train acc 0.836,test acc 0.806
'''
8.2 写法二
class LinearNet(torch.nn.Module):
def __init__(self, num_inputs, num_outputs):
super(LinearNet, self).__init__()
self.linear = torch.nn.Linear(num_inputs, num_outputs)
def forward(self, x): # x shape: (batch, 1, 28, 28)
y = self.linear(x.view(x.shape[0], -1))
return y
net = LinearNet(num_input, num_output)
# 定义优化器
optimizer = torch.optim.SGD(net2.parameters(),lr=0.1)
# 定义损失函数
loss = torch.nn.CrossEntropyLoss()
# 训练
train(net2,train_iter,test_iter,loss,5,batch_size,None,None,optimizer=optimizer)
9、多层感知机的实现
# loadDataset.py
# 用来将输入数据展开为一维
class FlattenLayer(torch.nn.Module):
def __init__(self):
super(FlattenLayer,self).__init__()
def forward(self,x):
y = x.view(x.shape[0],-1)
return y
# 用来把训练数据分成多个小组,此函数每次抛出一组数据
def load_data_fashion_mnist(batch_size):
mnist_train = torchvision.datasets.FashionMNIST(root='./Datasets', train=True, download=True,
transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='./Datasets', train=False, download=True,
transform=transforms.ToTensor())
# 获取小批量数据
# batch_size = 256
if sys.platform.startswith("win"):
num_works = 0 # 0表示不用额外的进程加速读取数据
else:
num_works = 4
train_iter = torch.utils.data.DataLoader(mnist_train,batch_size=batch_size,shuffle=True,num_workers=num_works)
test_iter = torch.utils.data.DataLoader(mnist_test,batch_size=batch_size,shuffle=True,num_workers=num_works)
return train_iter,test_iter
def train(net,train_iter,test_iter,loss,num_epochs,batch_size,params=None,lr=None,optimizer=None):
for epoch in range(num_epochs):
train_l_sum,train_acc_sum,n,batch_count = 0.0,0.0,0,0
for X,y in train_iter:
y_pre = net(X)
l = loss(y_pre,y).sum()
# 梯度清零
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
sgd(params,lr,batch_size)
else:
optimizer.step()
train_l_sum += l.item() # 训练损失之和
train_acc_sum += (y_pre.argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter,net)
print('epoch %d,loss %.4f,train acc %.3f,test acc %.3f'%(epoch+1,train_l_sum/batch_count,train_acc_sum/n,test_acc))
# main.py
import torch
import torch.nn as nn
from torch.nn import init
import loadDataset as LD
num_input,num_hidden,num_output = 784,256,10
batch_size = 256
net = nn.Sequential(
LD.FlattenLayer(),
nn.Linear(num_input,num_hidden),
nn.ReLU(),
nn.Linear(num_hidden,num_output),
)
for param in net.parameters():
init.normal_(param,mean=0,std=0.01)
train_iter,test_iter = LD.load_data_fashion_mnist(batch_size)
loss = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(),lr=0.1)
num_epochs = 5
LD.train(net,train_iter,test_iter,loss,num_epochs,batch_size,None,None,optimizer=optimizer)
四、深度学习计算
1、模型构造——module
1.1 Module的子类
- Sequential类
它可以接收一个子模块的有序字典(OrderedDict)或者一系列子模块作为参数来逐一添加Module的实例,而模型的前向计算就是将这些实例按添加的顺序逐一计算。
net = nn.Sequential(
nn.Linear(num_input,num_hidden),
nn.ReLU(),
nn.Linear(num_hidden,num_output),
)
- ModuleList类
接收一个子模块的列表作为输入,然后也可以类似List那样进行append和extend操作:
net = nn.ModuleList([nn.Linear(784, 256), nn.ReLU()])
net.append(nn.Linear(256, 10)) # # 类似List的append操作
print(net[-1]) # 类似List的索引访问
print(net)
# net(torch.zeros(1, 784)) # 会报NotImplementedError
和Sequential类的区别:(1)ModuleList仅仅是一个储存各种模块的列表,这些模块之间没有联系也没有顺序(2)没有实现forward(),需要手动实现
- ModuleDict类
接收一个子模块的字典作为输入, 然后也可以类似字典那样进行添加访问操作:
net = nn.ModuleDict({
'linear': nn.Linear(784, 256),
'act': nn.ReLU(),
})
net['output'] = nn.Linear(256, 10) # 添加
print(net['linear']) # 访问
print(net.output)
print(net)
# net(torch.zeros(1, 784)) # 会报NotImplementedError
和Sequential类的区别:(1)无序(2)没有实现forward()
1.2 小结
- 可以通过继承Module类来构造模型。
- Sequential、ModuleList、ModuleDict类都继承自Module类。
- 与Sequential不同,ModuleList和ModuleDict并没有定义一个完整的网络,它们只是将不同的模块存放在一起,需要自己定义forward函数。
- 虽然Sequential等类可以使模型构造更加简单,但直接继承Module类可以极大地拓展模型构造的灵活性。
2、读取和存储
2.1 存储tensor
存储单个tensor
import torch
x = torch.ones(4,4)
torch.save(x,"x.pt") # 存储为x.pt文件
x2 = torch.load("x.pt") # 从x.pt文件中读取
print(x2)
存储tensor列表
x = torch.ones(4,4)
y = torch.ones(3,3)
torch.save([x,y],"xy.pt")
x2 = torch.load("xy.pt")
print(x2)
存储tensor字典映射
x = torch.ones(4,4)
y = torch.ones(3,3)
torch.save({"x":x,"y":y},"xy.pt")
x2 = torch.load("xy.pt")
print(x2)
存储网络模型
2.2 存储网络模型
保存和加载state_dict(推荐方式)
# 保存
torch.save(model.state_dict(), PATH) # 推荐的文件后缀名是pt或pth
# 加载
model = TheModelClass(*args, **kwargs) # 初始化一个网络模型
model.load_state_dict(torch.load(PATH))
保存和加载整个模型
# 保存
torch.save(model, PATH)
# 加载
model = torch.load(PATH).
五、卷积神经网络
1、卷积运算
(f∗g)(n)为f,g的卷积
(f*g)(n)为f,g的卷积
(f∗g)(n)为f,g的卷积
其连续定义方式为:
(f∗g)(n)=∫−∞∞f(r)g(n−r)dr
(f*g)(n)=\int_{-\infty}^{\infty}f(r)g(n-r)dr
(f∗g)(n)=∫−∞∞f(r)g(n−r)dr
离散方式定义为:
(f∗g)(n)=∑r=−∞∞f(r)g(n−r)
(f*g)(n)=\sum_{r=-\infty}^{\infty}f(r)g(n-r)
(f∗g)(n)=r=−∞∑∞f(r)g(n−r)
2、互相关运算

0×0+1×1+3×2+4×3=19,
1×0+2×1+4×2+5×3=25,
3×0+4×1+6×2+7×3=37,
4×0+5×1+7×2+8×3=43.
深度学习中的卷积运算实际上是互相关运算!!!
像素之间的关系:
output_size = (input_size - kernel_size + 2 * padding) / stride + 1
3、LeNet网络
网络结构:

搭建网络:
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
nn.Sigmoid(),
nn.MaxPool2d(2, 2), # kernel_size, stride
nn.Conv2d(6, 16, 5),
nn.Sigmoid(),
nn.MaxPool2d(2, 2)
)
self.fc = nn.Sequential(
nn.Linear(16*4*4, 120),
nn.Sigmoid(),
nn.Linear(120, 84),
nn.Sigmoid(),
nn.Linear(84, 10)
)
def forward(self, img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0], -1))
return output
评估模型的精确性:
def evaluate_accuracy(data_iter, net, device=None):
if device is None and isinstance(net, torch.nn.Module): # device为空且net是Moudle的子类
# 如果没指定device就使用net的device
device = list(net.parameters())[0].device
acc_sum, n = 0.0, 0
with torch.no_grad():
for X, y in data_iter:
if isinstance(net, torch.nn.Module):
net.eval() # 评估模式, 这会关闭dropout(目的是测试网络而不是训练网络,没必要dropout一些参数)
acc_sum += (net(X.to(device)).argmax(dim=1) == y.to(device)).float().sum().cpu().item()
net.train() # 改回训练模式
else: # 如果是自定义的模型, 不考虑GPU
if('is_training' in net.__code__.co_varnames): # 如果有is_training这个参数
# 将is_training设置成False
acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item()
else:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
训练过程:
# 开始训练
def train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs):
net = net.to(device)
print("training on ", device)
loss = torch.nn.CrossEntropyLoss()
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n, batch_count, start = 0.0, 0.0, 0, 0, time.time()
for X, y in train_iter:
X = X.to(device)
y = y.to(device)
y_hat = net(X)
l = loss(y_hat, y) # 交叉熵函数包含了求和操作,返回包含一个元素的矩阵
optimizer.zero_grad()
l.backward()
optimizer.step()
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
batch_count += 1
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, time %.1f sec'
% (epoch + 1, train_l_sum / batch_count, train_acc_sum / n, test_acc, time.time() - start))
测试结果:
net = LeNet()
batch_size = 256
train_iter, test_iter = LD.load_data_fashion_mnist(batch_size)
lr, num_epochs = 0.01, 100
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
'''
输出:
training on cuda
epoch 1, loss 1.0959, train acc 0.574, test acc 0.755, time 12.1 sec
epoch 2, loss 0.5408, train acc 0.797, test acc 0.812, time 11.2 sec
epoch 3, loss 0.4330, train acc 0.839, test acc 0.845, time 11.1 sec
epoch 4, loss 0.3720, train acc 0.863, test acc 0.861, time 11.1 sec
epoch 5, loss 0.3346, train acc 0.876, test acc 0.873, time 11.3 sec
......
'''
4、AlexNet网络
网络结构:

搭建网络:
class AlexNet(nn.Module):
def __init__(self):
super(AlexNet, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(1, 96, 11, 4), # in_channels, out_channels, kernel_size, stride, padding
nn.ReLU(),
nn.MaxPool2d(3, 2), # kernel_size, stride
# 减小卷积窗口,使用填充为2来使得输入与输出的高和宽一致,且增大输出通道数
nn.Conv2d(96, 256, 5, 1, 2),
nn.ReLU(),
nn.MaxPool2d(3, 2),
# 连续3个卷积层,且使用更小的卷积窗口。除了最后的卷积层外,进一步增大了输出通道数。
# 前两个卷积层后不使用池化层来减小输入的高和宽
nn.Conv2d(256, 384, 3, 1, 1),
nn.ReLU(),
nn.Conv2d(384, 384, 3, 1, 1),
nn.ReLU(),
nn.Conv2d(384, 256, 3, 1, 1),
nn.ReLU(),
nn.MaxPool2d(3, 2)
)
# 这里全连接层的输出个数比LeNet中的大数倍。使用丢弃层来缓解过拟合
self.fc = nn.Sequential(
nn.Linear(256*5*5, 4096),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(4096, 4096),
nn.ReLU(),
nn.Dropout(0.5),
# 输出层。由于这里使用Fashion-MNIST,所以用类别数为10,而非论文中的1000
nn.Linear(4096, 10),
)
def forward(self, img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0], -1))
return output
载入数据集:
def load_data_fashion_mnist(batch_size, resize=None, root='./Datasets'):
"""Download the fashion mnist dataset and then load into memory."""
trans = []
if resize:
trans.append(torchvision.transforms.Resize(size=resize))
trans.append(torchvision.transforms.ToTensor())
transform = torchvision.transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=4)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=4)
return train_iter, test_iter
训练及结果:
if __name__=="__main__":
batch_size = 128
# 如出现“out of memory”的报错信息,可减小batch_size或resize
train_iter, test_iter = load_data_fashion_mnist(batch_size, resize=224)
net = AlexNet()
print("AlexNet")
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
'''
输出:
AlexNet
training on cuda
epoch 1, loss 0.6161, train acc 0.765, test acc 0.855, time 207.7 sec
epoch 2, loss 0.3388, train acc 0.873, test acc 0.886, time 212.1 sec
epoch 3, loss 0.2924, train acc 0.889, test acc 0.886, time 224.1 sec
epoch 4, loss 0.2643, train acc 0.901, test acc 0.905, time 223.9 sec
epoch 5, loss 0.2359, train acc 0.911, test acc 0.906, time 214.9 sec
'''
为方便起见,将获取数据集,评估精确率,训练的函数封装在util.py中供后面的网络直接调用
# util.py
import torch
import time
import torchvision
# 载入数据集,使用mnist,并对mnist数据图像进行resize放大到224*224
def load_data_fashion_mnist(batch_size, resize=None, root='./Datasets'):
"""Download the fashion mnist dataset and then load into memory."""
trans = []
if resize:
trans.append(torchvision.transforms.Resize(size=resize))
trans.append(torchvision.transforms.ToTensor())
transform = torchvision.transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=2)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=2)
return train_iter, test_iter
# 评估模型的准确率
def evaluate_accuracy(data_iter, net, device=None):
if device is None and isinstance(net, torch.nn.Module): # device为空且net是Moudle的子类
# 如果没指定device就使用net的device
device = list(net.parameters())[0].device
acc_sum, n = 0.0, 0
with torch.no_grad():
for X, y in data_iter:
if isinstance(net, torch.nn.Module):
net.eval() # 评估模式, 这会关闭dropout(目的是测试网络而不是训练网络,没必要dropout一些参数)
acc_sum += (net(X.to(device)).argmax(dim=1) == y.to(device)).float().sum().cpu().item()
net.train() # 改回训练模式
else: # 如果是自定义的模型, 不考虑GPU
if('is_training' in net.__code__.co_varnames): # 如果有is_training这个参数
# 将is_training设置成False
acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item()
else:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
# 开始训练
def train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs):
net = net.to(device)
print("training on ", device)
loss = torch.nn.CrossEntropyLoss()
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n, start = 0.0, 0.0, 0, time.time()
for X, y in train_iter:
X = X.to(device)
y = y.to(device)
y_hat = net(X)
l = loss(y_hat, y) # 交叉熵函数包含了求和操作,返回包含一个元素的矩阵
optimizer.zero_grad()
l.backward()
optimizer.step()
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, time %.1f sec'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc, time.time() - start))
# 用来将输入数据展开为一维
class FlattenLayer(torch.nn.Module):
def __init__(self):
super(FlattenLayer,self).__init__()
def forward(self,x):
y = x.view(x.shape[0],-1)
return y
5、VGG网络
VGG提出了可以通过重复使用简单的基础块来构造深度模型的思路
5.1 VGG块

代码实现:
def vgg_block(num_convs, in_channels, out_channels):
blk = []
for i in range(num_convs):
if i == 0:
blk.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
else:
blk.append(nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1))
blk.append(nn.ReLU())
blk.append(nn.MaxPool2d(kernel_size=2, stride=2)) # 这里会使宽高减半
return nn.Sequential(*blk)
5.2 VGG-11网络搭建
这个网络使用了8个卷积层和3个全连接层,所以经常被称为VGG -11
def vgg(conv_arch, fc_features, fc_hidden_units=4096):
net = nn.Sequential()
# 卷积层部分
for i, (num_convs, in_channels, out_channels) in enumerate(conv_arch):
# 每经过一个vgg_block都会使宽高减半
net.add_module("vgg_block_" + str(i+1), vgg_block(num_convs, in_channels, out_channels))
# 全连接层部分
net.add_module("fc", nn.Sequential(LD.FlattenLayer(),
nn.Linear(fc_features, fc_hidden_units),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(fc_hidden_units, fc_hidden_units),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(fc_hidden_units, 10)
))
return net
5.3 获取数据和训练VGG模型
if __name__ == '__main__':
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
conv_arch = ((1, 1, 64), (1, 64, 128), (2, 128, 256), (2, 256, 512), (2, 512, 512))
# 经过5个vgg_block, 宽高会减半5次, 变成 224/32 = 7
fc_features = 512 * 7 * 7 # c * w * h
fc_hidden_units = 4096 # 任意
# 构造一个高和宽取代224的单通道数据样本来观察每一层的输出形状
net = vgg(conv_arch, fc_features, fc_hidden_units)
X = torch.rand(1, 1, 224, 224)
# named_children获取一级子模块及其名字(named_modules会返回所有子模块,包括子模块的子模块)
# for name, blk in net.named_children():
# X = blk(X)
# print(name, 'output shape: ', X.shape)
# 因为VGG-11计算上比AlexNet更复杂,出于测试的目的我们构造一个通道数更小,或者说更窄的网络在时尚-MNIST数据集上进行训练。
ratio = 8
small_conv_arch = [(1, 1, 64 // ratio), (1, 64 // ratio, 128 // ratio), (2, 128 // ratio, 256 // ratio),
(2, 256 // ratio, 512 // ratio), (2, 512 // ratio, 512 // ratio)]
net = vgg(small_conv_arch, fc_features // ratio, fc_hidden_units // ratio)
# print(net)
batch_size = 64
# 如出现“out of memory”的报错信息,可减小batch_size
train_iter, test_iter = util.load_data_fashion_mnist(batch_size, 224)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
6、NiN网络
它提出了另外一个想法,即多个由卷积层和“全连接”层构成的小网络来构建一个深层网络
6.1 NiN块
左图是AlexNet和VGG的网络结构局部,右图是NiN的网络结构局部

代码实现:
def nin_block(in_channels, out_channels, kernel_size, stride, padding):
blk = nn.Sequential(nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding),
nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1),
nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1),
nn.ReLU())
return blk
6.2 NiN网络结构
net = nn.Sequential(
nin_block(1, 96, kernel_size=11, stride=4, padding=0),
nn.MaxPool2d(kernel_size=3, stride=2),
nin_block(96, 256, kernel_size=5, stride=1, padding=2),
nn.MaxPool2d(kernel_size=3, stride=2),
nin_block(256, 384, kernel_size=3, stride=1, padding=1),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Dropout(0.5),
# 标签类别数是10
nin_block(384, 10, kernel_size=3, stride=1, padding=1),
nn.AdaptiveAvgPool2d((1, 1)),
# 将四维的输出转成二维的输出,其形状为(批量大小, 10)
nn.Flatten()
# GlobalAvgPool2d(),
# # 将四维的输出转成二维的输出,其形状为(批量大小, 10)
# LD.FlattenLayer()
)
6.3 NiN网络训练
if __name__ == '__main__':
net = nn.Sequential(
nin_block(1, 96, kernel_size=11, stride=4, padding=0),
nn.MaxPool2d(kernel_size=3, stride=2),
nin_block(96, 256, kernel_size=5, stride=1, padding=2),
nn.MaxPool2d(kernel_size=3, stride=2),
nin_block(256, 384, kernel_size=3, stride=1, padding=1),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Dropout(0.5),
# 标签类别数是10
nin_block(384, 10, kernel_size=3, stride=1, padding=1),
nn.AdaptiveAvgPool2d((1, 1)),
# 将四维的输出转成二维的输出,其形状为(批量大小, 10)
nn.Flatten()
# GlobalAvgPool2d(),
# # 将四维的输出转成二维的输出,其形状为(批量大小, 10)
# LD.FlattenLayer()
)
# 查看每一层形状
# X = torch.rand(1, 1, 224, 224)
# for name, blk in net.named_children():
# X = blk(X)
# print(name, 'output shape: ', X.shape)
batch_size = 32
# 如出现“out of memory”的报错信息,可减小batch_size或resize
train_iter, test_iter = util.load_data_fashion_mnist(batch_size,224)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
lr, num_epochs = 0.002, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
util.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
7、GoogLeNet网络
GoogLeNet吸收了NiN中网络串联网络的思想,并在此基础上做了很大改进。
7.1 Inception 块

4条线路都使用了合适的填充来使输入与输出的高和宽一致。最后我们将每条线路的输出在通道维上连结,并输入接下来的层中去。
代码实现:
import torch
from torch import nn
import torch.nn.functional as F
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 定义Inception块
class Inception(nn.Module):
# c1 - c4为每条线路里的层的输出通道数
def __init__(self, in_c, c1, c2, c3, c4):
super(Inception, self).__init__()
# 线路1,单1 x 1卷积层
self.p1_1 = nn.Conv2d(in_c, c1, kernel_size=1)
# 线路2,1 x 1卷积层后接3 x 3卷积层
self.p2_1 = nn.Conv2d(in_c, c2[0], kernel_size=1)
self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
# 线路3,1 x 1卷积层后接5 x 5卷积层
self.p3_1 = nn.Conv2d(in_c, c3[0], kernel_size=1)
self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
# 线路4,3 x 3最大池化层后接1 x 1卷积层
self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
self.p4_2 = nn.Conv2d(in_c, c4, kernel_size=1)
def forward(self, x):
p1 = F.relu(self.p1_1(x))
p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
p4 = F.relu(self.p4_2(self.p4_1(x)))
return torch.cat((p1, p2, p3, p4), dim=1) # 在通道维上连结输出
7.2 GoogLeNet网络结构
在主体卷积部分中使用5个模块(block),每个模块之间使用步幅为2的3×3最大池化层来减小输出高宽。
第一个模块
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
第二个模块
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
nn.Conv2d(64, 192, kernel_size=3, padding=1),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
第三个模块
串联2个完整的Inception块。
第一个Inception块的输出通道数为64+128+32+32=256,其中第二、第三条线路先分别将输入通道数减小至96/192=1/2后,再接上第二层卷积层;
第二个Inception块输出通道数增至128+192+96+64=480,其中第二、第三条线路先分别将输入通道数减小至128/256=1/2和32/256=1/8。
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
Inception(256, 128, (128, 192), (32, 96), 64),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
第四个模块
第四模块串联了5个Inception块,其输出通道数分别是192+208+48+64=512、160+224+64+64=512、128+256+64+64=512、112+288+64+64=528和256+320+128+128=832。
这些线路的通道数分配和第三模块中的类似,首先含3×3卷积层的第二条线路输出最多通道,其次是仅含1×1卷积层的第一条线路,之后是含5×5卷积层的第三条线路和含3×3最大池化层的第四条线路。其中第二、第三条线路都会先按比例减小通道数。
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
Inception(512, 160, (112, 224), (24, 64), 64),
Inception(512, 128, (128, 256), (24, 64), 64),
Inception(512, 112, (144, 288), (32, 64), 64),
Inception(528, 256, (160, 320), (32, 128), 128),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
第五个模块
第五模块有输出通道数为256+320+128+128=832和384+384+128+128=1024的两个Inception块。
其中每条线路的通道数的分配思路和第三、第四模块中的一致,只是在具体数值上有所不同。需要注意的是,第五模块的后面紧跟输出层,该模块同NiN一样使用全局平均池化层来将每个通道的高和宽变成1。最后我们将输出变成二维数组后接上一个输出个数为标签类别数的全连接层。
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
Inception(832, 384, (192, 384), (48, 128), 128),
util.GlobalAvgPool2d())
net = nn.Sequential(b1, b2, b3, b4, b5,
util.FlattenLayer(), nn.Linear(1024, 10))
代码实现:
class GoogLeNet(nn.Module):
def __init__(self):
super(GoogLeNet,self).__init__()
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
nn.Conv2d(64, 192, kernel_size=3, padding=1),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
Inception(256, 128, (128, 192), (32, 96), 64),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
Inception(512, 160, (112, 224), (24, 64), 64),
Inception(512, 128, (128, 256), (24, 64), 64),
Inception(512, 112, (144, 288), (32, 64), 64),
Inception(528, 256, (160, 320), (32, 128), 128),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
Inception(832, 384, (192, 384), (48, 128), 128),
util.GlobalAvgPool2d())
self.net = nn.Sequential(b1, b2, b3, b4, b5,
util.FlattenLayer(), nn.Linear(1024, 10))
def forward(self,X):
out = self.net(X)
return out
7.2 GoogLeNet训练
if __name__ == '__main__':
# b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
# nn.ReLU(),
# nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
#
# b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
# nn.Conv2d(64, 192, kernel_size=3, padding=1),
# nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
#
# b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
# Inception(256, 128, (128, 192), (32, 96), 64),
# nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
#
# b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
# Inception(512, 160, (112, 224), (24, 64), 64),
# Inception(512, 128, (128, 256), (24, 64), 64),
# Inception(512, 112, (144, 288), (32, 64), 64),
# Inception(528, 256, (160, 320), (32, 128), 128),
# nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
#
# b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
# Inception(832, 384, (192, 384), (48, 128), 128),
# util.GlobalAvgPool2d())
# net = nn.Sequential(b1, b2, b3, b4, b5,
# util.FlattenLayer(), nn.Linear(1024, 10))
net = GoogLeNet()
batch_size = 128
# 如出现“out of memory”的报错信息,可减小batch_size或resize
train_iter, test_iter = util.load_data_fashion_mnist(batch_size, resize=96)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
util.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
8、BN层(批量归一化)
批量归一化(batch normalization)层,它能让较深的神经网络的训练变得更加容易,为残差网络为训练和设计深度模型提供了两类重要思路。
对全连接层和卷积层做批量归一化的方法稍有不同。下面分别介绍这两种情况下的批量归一化。
8.1 全连接层归一化
设输入为u,权重参数和偏差参数分别为W和b,激活函数为φ,归一化操作为BN,则输出为:

其中 x 由以下得到:

对于小批量样本仿射变换输入,有:

BN操作的具体步骤为:
- 先求输入样本的均值和方差

-
对样本进行标准化(其中 ϵ >0,是一个非常小的常数)

-
引入了两个可以学习的模型参数,拉伸(scale)参数 γ 和偏移(shift)参数 β 进行学习,并得到归一化结果 y

注: 若学出
 则说明理论上,学出的模型可以不使用批量归一化
则说明理论上,学出的模型可以不使用批量归一化
8.2 卷积层归一化
- 对卷积层来说,批量归一化发生在卷积计算之后、应用激活函数之前。如果卷积计算输出多个通道,我们需要对这些通道的输出分别做批量归一化,且每个通道都拥有独立的拉伸和偏移参数,并均为标量。
- 设小批量中有m个样本。在单个通道上,假设卷积计算输出的高和宽分别为p和q。我们需要对该通道中m×p×q个元素同时做批量归一化。对这些元素做标准化计算时,我们使用相同的均值和方差,即该通道中m×p×q个元素的均值和方差。
8.3 预测时的批量归一化
-
使用批量归一化训练时,可以将批量大小设得大一点,从而使批量内样本的均值和方差的计算都较为准确。
-
将训练好的模型用于预测时,希望模型对于任意输入都有确定的输出。因此,单个样本的输出不应取决于批量归一化所需要的随机小批量中的均值和方差。一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差,并在预测时使用它们得到确定的输出。
*8.4 从零开始实现批量归一化层
import torch
from torch import nn
import util
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 批量归一化操作
def batch_norm(is_training, X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 判断当前模式是训练模式还是预测模式
if not is_training:
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean) ** 2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。这里我们需要保持
# X的形状以便后面可以做广播运算
mean = X.mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
var = ((X - mean) ** 2).mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
# 训练模式下用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 拉伸和偏移
return Y, moving_mean, moving_var
class BatchNorm(nn.Module):
def __init__(self, num_features, num_dims):
super(BatchNorm, self).__init__()
if num_dims == 2:
shape = (1, num_features)
else:
shape = (1, num_features, 1, 1)
# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成0和1
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
# 不参与求梯度和迭代的变量,全在内存上初始化成0
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.zeros(shape)
def forward(self, X):
# 如果X不在内存上,将moving_mean和moving_var复制到X所在显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的moving_mean和moving_var, Module实例的traning属性默认为true, 调用.eval()后设成false
Y, self.moving_mean, self.moving_var = batch_norm(self.training,
X, self.gamma, self.beta, self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.9)
return Y
if __name__=="__main__":
# 一个使用添加了BN层的LeNet网络
net = nn.Sequential(
nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
BatchNorm(6, num_dims=4),
nn.Sigmoid(),
nn.MaxPool2d(2, 2), # kernel_size, stride
nn.Conv2d(6, 16, 5),
BatchNorm(16, num_dims=4),
nn.Sigmoid(),
nn.MaxPool2d(2, 2),
util.FlattenLayer(),
nn.Linear(16 * 4 * 4, 120),
BatchNorm(120, num_dims=2),
nn.Sigmoid(),
nn.Linear(120, 84),
BatchNorm(84, num_dims=2),
nn.Sigmoid(),
nn.Linear(84, 10)
)
batch_size = 256
train_iter, test_iter = util.load_data_fashion_mnist(batch_size=batch_size)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
util.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
8.5 使用pytorch简洁实现
Pytorch中nn模块定义的BatchNorm1d类和BatchNorm2d类使用起来更加简单,二者分别用于全连接层和卷积层,都需要指定输入的num_features参数值。
net = nn.Sequential(
nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
nn.BatchNorm2d(6),
nn.Sigmoid(),
nn.MaxPool2d(2, 2), # kernel_size, stride
nn.Conv2d(6, 16, 5),
nn.BatchNorm2d(16),
nn.Sigmoid(),
nn.MaxPool2d(2, 2),
util.FlattenLayer(),
nn.Linear(16 * 4 * 4, 120),
nn.BatchNorm1d(120),
nn.Sigmoid(),
nn.Linear(120, 84),
nn.BatchNorm1d(84),
nn.Sigmoid(),
nn.Linear(84, 10)
)
9、残差网络(ResNet)
对神经网络模型添加新的层,原模型解的空间只是新模型解的空间的子空间。由于新模型可能得出更优的解来拟合训练数据集,因此添加层似乎更容易降低训练误差。然而在实践中,添加过多的层后训练误差往往不降反升。即使利用批量归一化带来的数值稳定性使训练深层模型更加容易,该问题仍然存在。针对这一问题,何恺明等人提出了残差网络。
9.1 残差块
普通的网络结构(左)与加入残差连接的网络结构(右)

设输入为x。假设我们希望学出的理想映射为f(x),从而作为图5.9上方激活函数的输入。左图虚线框中的部分需要直接拟合出该映射f(x),而右图虚线框中的部分则需要拟合出有关恒等映射的残差映射f(x)−x。残差映射在实际中往往更容易优化。
代码实现:
# 残差结构
class Residual(nn.Module): # 本类已保存在util包中方便以后使用
def __init__(self, in_channels, out_channels, use_1x1conv=False, stride=1):
super(Residual, self).__init__()
self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1, stride=stride)
self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(out_channels)
self.bn2 = nn.BatchNorm2d(out_channels)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
return F.relu(Y + X) #这里的Y被拟合为F(x)-x
# 残差块
def resnet_block(in_channels, out_channels, num_residuals, first_block=False):
if first_block:
assert in_channels == out_channels # 第一个模块的通道数同输入通道数一致
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(Residual(in_channels, out_channels, use_1x1conv=True, stride=2))
else:
blk.append(Residual(out_channels, out_channels))
return nn.Sequential(*blk)
9.2 残差网络的搭建与训练
if __name__=="__main__":
net = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
net.add_module("resnet_block1", resnet_block(64, 64, 2, first_block=True))
net.add_module("resnet_block2", resnet_block(64, 128, 2))
net.add_module("resnet_block3", resnet_block(128, 256, 2))
net.add_module("resnet_block4", resnet_block(256, 512, 2))
net.add_module("global_avg_pool", util.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, 512, 1, 1)
net.add_module("fc", nn.Sequential(util.FlattenLayer(), nn.Linear(512, 10)))
batch_size = 256
# 如出现“out of memory”的报错信息,可减小batch_size或resize
train_iter, test_iter = util.load_data_fashion_mnist(batch_size, resize=96)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
util.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
10、稠密连接网络(DenseNet)
稠密网络和残差网络的思想大致相同,稠密网络将残差网络中的相加改为了相连接。网络结构如下图所示:
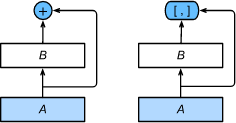
ResNet(左)与DenseNet(右)
与ResNet的主要区别在于,DenseNet里模块BB的输出不是像ResNet那样和模块A的输出相加,而是在通道维上连结。这样模块A的输出可以直接传入模块B后面的层。在这个设计里,模块A直接跟模块B后面的所有层连接在了一起。这也是它被称为“稠密连接”的原因。
10.1 稠密快
代码实现:
# DenseNet使用了ResNet改良版的“批量归一化、激活和卷积”结构
def conv_block(in_channels, out_channels):
blk = nn.Sequential(nn.BatchNorm2d(in_channels),
nn.ReLU(),
nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
return blk
# 稠密块
class DenseBlock(nn.Module):
def __init__(self, num_convs, in_channels, out_channels):
super(DenseBlock, self).__init__()
net = []
for i in range(num_convs):
in_c = in_channels + i * out_channels
net.append(conv_block(in_c, out_channels))
self.net = nn.ModuleList(net)
self.out_channels = in_channels + num_convs * out_channels # 计算输出通道数
def forward(self, X):
for blk in self.net:
Y = blk(X)
X = torch.cat((X, Y), dim=1) # 在通道维上将输入和输出连结
return X
10.2 过渡层
通过1×1卷积层来减小通道数,并使用步幅为2的平均池化层减半高和宽,从而降低模型复杂度。
代码实现:
def transition_block(in_channels, out_channels):
blk = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.ReLU(),
nn.Conv2d(in_channels, out_channels, kernel_size=1),
nn.AvgPool2d(kernel_size=2, stride=2))
return blk
10.3 稠密网络的搭建与训练
if __name__ == '__main__':
# 首先使用同ResNet一样的单卷积层和最大池化层
net = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
# 类似于ResNet接下来使用的4个残差块,DenseNet使用的是4个稠密块
num_channels, growth_rate = 64, 32 # num_channels为当前的通道数
num_convs_in_dense_blocks = [4, 4, 4, 4]
for i, num_convs in enumerate(num_convs_in_dense_blocks):
DB = DenseBlock(num_convs, num_channels, growth_rate) # 每个稠密块将增加128个通道
net.add_module("DenseBlosk_%d" % i, DB)
# 上一个稠密块的输出通道数
num_channels = DB.out_channels
# 在稠密块之间加入通道数减半的过渡层
if i != len(num_convs_in_dense_blocks) - 1:
net.add_module("transition_block_%d" % i, transition_block(num_channels, num_channels // 2))
num_channels = num_channels // 2
# 同ResNet一样,最后接上全局池化层和全连接层来输出
net.add_module("BN", nn.BatchNorm2d(num_channels))
net.add_module("relu", nn.ReLU())
net.add_module("global_avg_pool", util.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, num_channels, 1, 1)
net.add_module("fc", nn.Sequential(util.FlattenLayer(), nn.Linear(num_channels, 10)))
# 获取数据集并训练
batch_size = 256
# 如出现“out of memory”的报错信息,可减小batch_size或resize
train_iter, test_iter = util.load_data_fashion_mnist(batch_size, resize=96)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
util.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
参考:
https://github.com/ShusenTang/Dive-into-DL-PyTorch





















 375
375

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








