模板笔记 ST表 区间选数k

本题链接：用户登录

题目：

样例：

输入

5 3 1 1 2 2 3 1 2 3 3 1 5

输出

4 6

思路：

.        根据题意，给出数组，以及多个区间，问这些区间中，最小值之和 和 最大值之和，分别是多少。

        由于题目中的数组元素是静态性的，典型的 RMQ 问题，给出元素，以及区间，进行询问即可。当然这里也是可以 使用 线段树进行求解，由于这道题是静态性的，所以我们可以直接使用 ST 表 的数据结构，进行求解即可。

线段树 的方式 是 可以解决动态性的 ，也可以解决静态性的，即线段树可以 边修改元素边询问。

ST 表 的方式 是 对口静态性的， 即 只能询问，不可以修改。

        根据这题，我们 “对症下药” 使用 ST表 方式方便些。

       

        ST 表 ，是 典型的 RMQ 数据结构，采用的是 倍增 思想。

        倍增，顾名思义，就是以2幂的成倍的增长。

        其中的核心思想就是：

        通过记录每一个区间的前半段和后半段，

        达到省略询问 重叠的区间，随后返回这些区间的最值

        ST 表类似 动态规划 dp ，根据 倍增关系得到的公式 i +  - 1

        我们假设得到一个区间 中的左端点 l  = i  ， 那么 根据 倍增 ，我们右端点   r = i +  - 1

        这里  r = i +  - 1  中  -1 是维护闭区间。

        

        随后，求这个区间的最值，我们可以截取 前半段 和 后半段的最值记录好对应的区间的最值

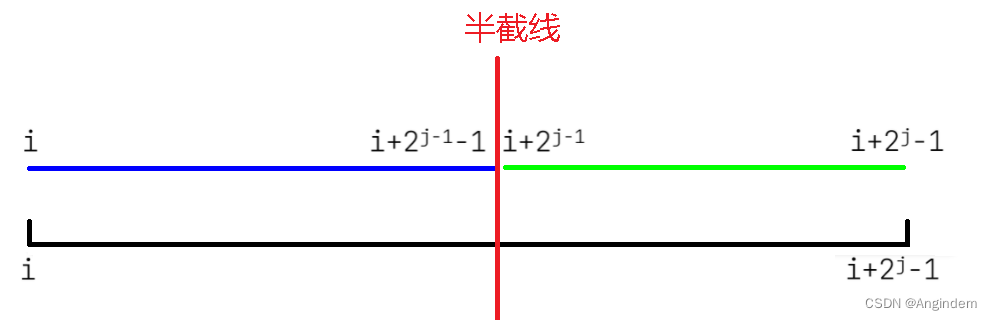
 随后当求到我们整个  i 到 i +  - 1 的最值的时候

我们 取个 max 或者 min （st(i,i +  - 1)  , st(i,i + ,i +  - 1)）即可。

这样省略的整个区间的求法，解决重叠部分的求最值。

我们假设 求的区间长度 为 K，则 K = R - L + 1，其中 2的次幂作为我们的截半端点的时候一定是

 <= K    &&       > K / 2  ,所以它们两个不部分有一个极限点重叠，所以我们取max和min两个部分的相应最值，相当于求 区间（L,R） 的最值。

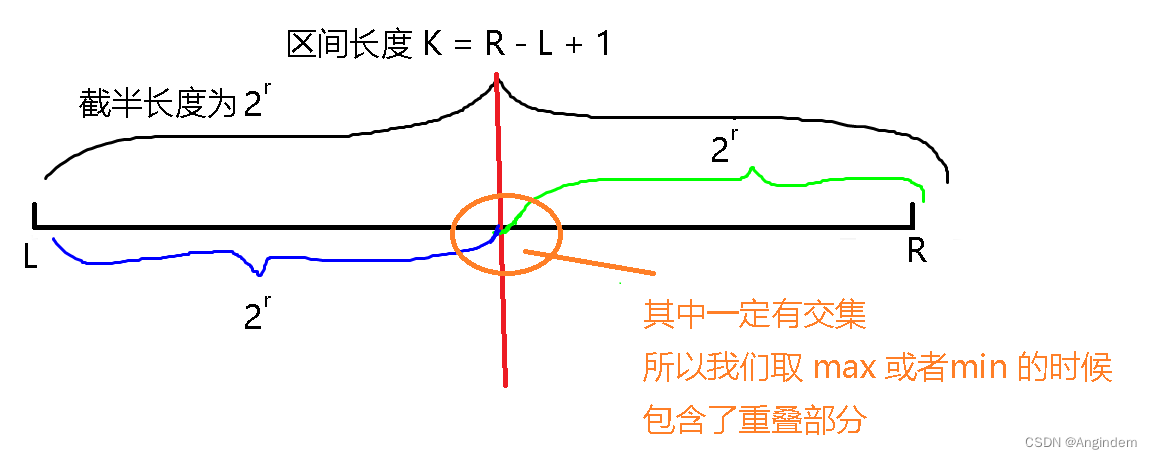
由上图，根据   = len(截半长度，右端点) 所以我们取右端点的值就是 r =     。

所以我们要对右端点预处理即可得到各个右端点。

模板函数如下：

const int N = 2e5 + 10;
int v[N],n,q;
int stmin[N][22],stmax[N][22];
inline void Init()
{
	for(int i = 1;i <= n;++i) stmin[i][0] = stmax[i][0] = v[i];
	
	for(int j = 1;j <= log2(n);++j)
	{
		for(int i = 1;i + (1 << j) - 1 <= n;++i)
		{
			int r = i + (1 << j - 1);
			stmin[i][j] = min(stmin[i][j - 1],stmin[r][j - 1]);
			stmax[i][j] = max(stmax[i][j - 1],stmax[r][j - 1]);
		}
	}
}
inline int rmq_min(int L,int R)
{
	int k = log2(R - L + 1);
	int len = (1 << k);
	int r = R - len + 1;
	return min(stmin[L][k],stmin[r][k]);
}
inline int rmq_max(int L,int R)
{
	int k = log2(R - L + 1);
	int len = (1 << k);
	int r = R - len + 1;
	return max(stmax[L][k],stmax[r][k]);
}

代码详解如下：

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <cmath>
#define endl '\n'
#include <unordered_map>
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e5 + 10;


// 这是个二维数组 可以理解为 int[][]  其中这个二维数组存储的是 对应的 R  和   r
// 其中 一维 int[] 存储的是 原端点 R      二维 int[][] 存储的是 截半右端点 r 至于为何 r 开 22 ，
// 这个是由于我们 是 log 以 2 为底、长度为基的数值 得到的右端点，所以我们开存在于我们范围内即可
int st_min[N][22],st_max[N][22];
int v[N]; // 存储原数组元素
int n,q;

inline void Init()
{
    // 预处理求出当前点的 右端点 R
    for(int i = 1;i <= n;++i)
    {
        // 这里是 当 左右端点相同的时候 它们的最值等于它们本身
        // 即 ： L == R 没有截半，截半端点r = 0
        st_min[i][0] = st_max[i][0] = v[i];
    }

    // 开始求每个截半区间的最值
    for(int R = 1;R <= log2(n);++R) // 这是区间右端点 R
    {
        // 截半区间前提是 截半的右端点 r 区间长度 不超过我们整个数组的区间长度
        for(int L = 1;L + (1 << R) - 1 <= n;++L)
        {
            int r = L + (1 << R - 1); // 截半右端点的 r

            // DP 递推公式   截半区间向右扩展对应的最值，
            // 当前的区间右端点 R 最值  =  (max or min) [之前的截半最值（L, R - 1 ）, 现在截半最值(r ，len - 1)]
            // 这样一步一步的递推下去，覆盖重叠部分的区间,记录好对应的截半区间的最值
			st_max[L][R] = max(st_max[L][R - 1],st_max[r][R - 1]); 
            st_min[L][R] = min(st_min[L][R - 1],st_min[r][R - 1]); 
        }
    }
}

inline int rmq_max(int L,int R)
{
    int k = log2(R - L + 1); // 取出对应的截半区间的原右端点
    
    int len = (1 << k);	//截半区间长度
    
    int r = R - len + 1; // 取出对应的截半右端点 r
    
    // 返回这两个截半区间的最值， 等于我们所求的 L ，R 的最值
    return  max(st_max[L][k],st_max[r][k]); 
}

inline int rmq_min(int L,int R)
{
    int k = log2(R - L + 1); // 取出对应的截半区间的原右端点
    
    int len = (1 << k);	//截半区间长度
    
    int r = R - len + 1; // 取出对应的截半右端点 r
    
    // 返回这两个截半区间的最值， 等于我们所求的 L ，R 的最值
    return  min(st_min[L][k],st_min[r][k]); 
}

inline void solve()
{
	cin >> n >> q;
	
	for(int i = 1;i <= n;++i) cin >> v[i];
	
	Init(); // 开始预处理 ST表 初始化
	
	// 存储答案
	int minsum = 0;
	int maxsum = 0;
	
	while(q--)
	{
	int l,r;
	cin >> l >> r;
	
	// 询问累加最值
	minsum += rmq_min(l,r);
	maxsum += rmq_max(l,r);
	
	}
	cout << minsum << ' ' << maxsum << endl;
}

signed main()
{
//	freopen("a.txt", "r", stdin);
	IOS;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}

最后提交：