区间问题+简单版线段树+ST表
对于某些区间问题:
一. 每组操作次数很大10^5且查询范围广的情况下可以考虑该区间的最大值和最小值,要求达到每个操作只进行一步就可以出结果。
- ST表是一种能够很好地完成一种特定的RMQ(区间最值问题)的算法。
ST表只能用来求静态区间的最大值和最小值问题:并且可以两个2^ k大小的区间,k代表查询的这段区间[l,r]在ST表中应该的第几层(k=log(r-l+1))。
预处理ST表的时间复杂的为O(nlogn),对于区间处理的时间复杂度O(1)。
下面会用图表模拟ST表的构造,以及更新方式
图像模拟:n=8,序列为 9 3 1 7 5 6 0 8 模拟出来的表
在第i行的第k个位置代表这从k到(k+2^i-1)的范围内最大值
且第i行表示这个区间的长度为2^i。
更新的方式为这一行 i 的m位置代表从(上一行m位置的最大值,上一行m+2^(i-1)位置最大值)比较的最大值作为 i 行的m位置的值(从m到m+2^i-1)范围的最大值

预处理ST表代码实现:
cin>>n>>m;先输入一个序列然后有m个询问
int t=n,k=0;
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
}
while(t!=1) {
t/=2;
k++;
}//求出的k为n这个数最大的二进制位也就是2^k<=n(k的最大值)
for(int i=1; i<=n; i++)
st[0][i]=a[i];//处理st表第一行也就是自己与自己比较,然后保存下来
for(int i=1; (1<<i)<=n; i++) {//这里用了二进制位运算就不用k了,当然也可以把中间的条件改成i<=k
for(int j=1; j<=n-pow(2,i)+1; j++) {
//这两层for循环的主要目的是更新从i的这位置到第i+pow(2,i-1)这区间的最大值
st[i][j]=max(st[i-1][j],st[i-1][j+(1<<(i-1))]);
//把上一行两个相邻的两个区间的max合成该行相对应的一个区间的max
}
}
使用其进行查询 [l, r]的最值查询
scanf("%d%d",&l,&r);
int ans1=r-l+1;//l到r区间的大小
t=ans1,k=0;
while(t!=1) {
t/=2;//看看ans1这个区间大小最大在第几层
k++;
}
int num=r-pow(2,k)+1;//这里存在一个小优化就是把这个不满足到下一层的区间,
//从头和尾重叠一部分,化为两个长度为2^k的区间,在比较这俩个区间的最大值
int first=st[k][l],second=st[k][num];
//first表示从[l,l+2^k-1] 范围的最大值,second表示从[r-2^k+1,r]范围的最大值
ans1=max(first,second);//比较两个区间得出结果
printf("%d\n",ans1);
- 线段树可以处理动态表也可以处理静态表的区间最大值和最小值问题。
建树的时间复杂度为O(nlogn),修改线段树的时间复杂度约为O(1),查找线段树区间O(1);
线段树可以解决区间最值问题,区间求和问题与区间乘一个数在求和问题。
线段树的优点:
1)建树,修改,查询的时间复杂度不是很大。
2)相当于一个二叉树的建立。
3)线段树是“分治法思想 + 二叉树结构 + lazy-tag技术的结合。
下面让我们一起来看看这个过程
首先咱们要先把线段树建立出来:
以数列{1, 4, 5, 8, 6, 2, 3, 9, 10, 7}为例,观察一下这棵树我们可以发现几个特点。
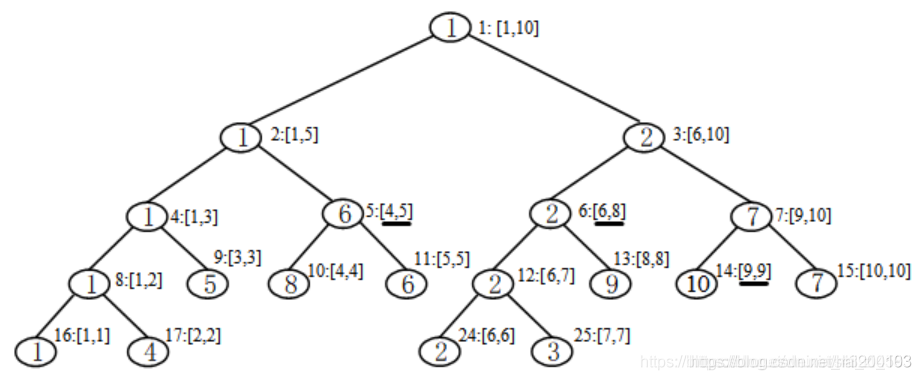
(1)树用分治法自上而下建立,每个节点把区间分为两半,左右子树各一半。
(2)每个节点表示一个线段,非子节点包含多个元素,叶子节点仅包含一个元素。
(3)除了最后一层其他都是满的,这种结构的树层数是最少的。
(4) 先到子节点再往会递归求父节点的值
建树实现本篇博客选择的是第二种方法建树。
//定义根结点是tree[1],即编号为1的结点是根
//(1)第一种方法:定义二叉树数据结构
struct{
int L, R, data; //用tree[i].data记录线段i的最值或区间和
}tree[MAXN*4]; //分配静态数组,开4倍大
//(2)第二种方法:直接用数组表示二叉树,更节省空间
int tree[MAXN*4]; //用tree[i]记录线段i的最值或区间和
//以上两种方式,都满足下面的父子关系。结点p是父,结点ls(p)是左儿子,rs(p)是右儿子
int ls(int x){ return x<<1; } //左儿子,编号是 p*2
int rs(int x){ return x<<1|1;} //右儿子,编号是 p*2+1
void push_up(int p){
tree[p]=tree[ls(p)]+tree[rs(p)];//求和树
//tree[p]=max(tree[ls(p)],tree[rs(p)]); //最大树
}
void build(int p,int pl,int pr){
tag[p]=0;//标记等会用于区间修改,没有的话,修改区间时间复杂度暴增
if(pr==pl){tree[p] = a[pl];return ;}//找到叶子节点
int mid = (pl+pr)>>1//分治:折半
build (ls(p),pl,mid); //递归左儿子
build (rs(p),mid+1,pr);//递归右儿子
push_up(p);
}
注意,二叉树的空间需要开MAXN*4,即元素数量的4倍,下面说明原因。假设有一棵处理n个元素(叶子结点有n个)的线段树,且它的最后一层只有1个叶子,其他层都是满的;如果用满二叉树表示,它的结点总数是:最后一层有2n个结点(其中2n - 1个都浪费了没用到),前面所有的层有2n个结点,共4n个结点。空间的浪费是二叉树的本质决定的:它的每一层都按2倍递增。
这里就不另外写单点修改了,直接区间修改,因为区间修改包括单点修改:
void addtag(int p,int pl,int pr,int d){
tag[p]+=d;//利用标题更新
tree[p]+=(pr-pl+1)*d;//这是用于把一个区间的每个数乘一个d
//tree[p]*=d; //这是用于把区间的每一个数乘一个d
}
void push_down(int p,int pl,int pr){
if(tag[p]){//把标记分给传给子节点
int mid = (pl + pr)>>1;
addtag(ls(p),pl,mid,tag[p]);
addtag(rs(p),mid + 1,pr,tag[p]);
tag[p]=0;
}
}
void update(int L,int R, int p,int pl,int pr,int d){
if(L <= pl && pr <= R){
addtag(p,pl,pr,d);//符合条件的区间标记一下
return ;
}
push_down(p,pl,pr);
int mid = (pl+pr) >> 1;
if(L <= mid)update(L,R,ls(p),pl,mid,d);
if(R > mid)update(L,R,rs(p),mid + 1,pr,d);
push_up(p);//从子节点向上更新
// 使用方法update(l,r,1,1,n,d);
}
查询的方法:假如要查询区间[lL,R];
我们先从最大的区间[1,n]>[L,R],二分区间,分成[1,n/2],[n/2,n];直到[L,R]包含子区间。
ll query(int L,int R,int p,int pl,int pr){
ll res=0;
if(L<=pl&&pr<=R)return tree[p];//完全覆盖在范围内
push_down(p,pl,pr);
int mid =(pl + pr) >> 1;
if(L <= mid) res += query(L, R, ls(p), pl, mid);//L与左子节点有重叠 ,用于求和
if(R > mid) res += query(L, R, rs(p), mid+1, pr);//R与右子节点有重叠
//if(L<=mid) res=max(res,query(L,R,ls(p),pl,mid));//“//注销的”用于区间最大值
//if(R>mid) res=max(res,query(L,R,rs(p),mid+1,pr));
return res;
}
//使用方法query(l,r,1,1,n);
- 下面讲的是最大值与最小值的一种区间求法 ,不常见。有些可以利用前缀维护[0-x]这段范围里的最大值与最小值,后缀和维护从最后面的位置(n)到某个位置(y)这段范围里的最大值与最小值。
针对上次练习题:两段分开的区间的总的max((前缀和最大值),前缀和+后缀和(后面一段区间的差值)-后缀最小值);
同理:两段分开的区间的总的min((前缀和最小值),前缀和+后缀和(后面一段区间的差值)-后缀最大值);
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i]=sum[i-1]+(a[i]=='+'?1:-1);
maxl[i]=max(maxl[i-1],sum[i]);
minl[i]=min(minl[i-1],sum[i]);
}
sumr[n+1]=0;maxr[n+1]=0;minr[n+1]=0;
for(int i=n;i>=1;i--){
sumr[i]=sumr[i+1]+((a[i]=='+'?1:-1));
maxr[i]=max(maxr[i+1],sumr[i]);
minr[i]=min(minr[i+1],sumr[i]);
}
int l,r;
for(int i=1;i<=m;i++){
cin>>l>>r;
int ans=max(maxl[l-1],sum[l-1]+sumr[r+1]-minr[r+1])
-min(minl[l-1],sum[l-1]+sumr[r+1]-maxr[r+1])+1;
}
二 .
1.线段树基础题解
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1000100;
ll a[N],tree[N*4],res=0,tag[N]={0};
int ls(int x){ return x*2;}
int rs(int x){ return (x<<1)+1;}
void push_up(int p){
tree[p]=tree[ls(p)]+tree[rs(p)];//求和树
//tree[p]=max(tree[ls(p)],tree[rs(p)]); //最大树
}
void build(int p,int pl,int pr){
tag[p]=0;
if(pr==pl){tree[p] = a[pl];return ;}
int mid = (pl+pr)>>1;
build (ls(p),pl,mid);
build (rs(p),mid+1,pr);
push_up(p);
}
void addtag(int p,int pl,int pr,int d){
tag[p]+=d;
tree[p]+=(pr-pl+1)*d;//这是用于把一个区间的每个数乘一个d
//tree[p]*=d; //这是用于把区间的每一个数乘一个d
}
void push_down(int p,int pl,int pr){
if(tag[p]){//把标记分给传给子节点
int mid = (pl + pr)>>1;
addtag(ls(p),pl,mid,tag[p]);
addtag(rs(p),mid + 1,pr,tag[p]);
tag[p]=0;
}
}
void update(int L,int R, int p,int pl,int pr,int d){
if(L <= pl && pr <= R){
addtag(p,pl,pr,d);//符合条件的区间标记一下
return ;
}
push_down(p,pl,pr);
int mid = (pl+pr) >> 1;
if(L <= mid)update(L,R,ls(p),pl,mid,d);
if(R > mid)update(L,R,rs(p),mid + 1,pr,d);
push_up(p);
}
ll query(int L,int R,int p,int pl,int pr){
ll res=0;
if(L<=pl&&pr<=R)return tree[p];//完全覆盖在范围内
push_down(p,pl,pr);
int mid =(pl + pr) >> 1;
if(L <= mid) res += query(L, R, ls(p), pl, mid);//L与左子节点有重叠 ,用于求和
if(R > mid) res += query(L, R, rs(p), mid+1, pr);//R与右子节点有重叠
//if(L<=mid) res=max(res,query(L,R,ls(p),pl,mid));//“//注销的”用于区间最大值
//if(R>mid) res=max(res,query(L,R,rs(p),mid+1,pr));
return res;
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
build(1,1,n);
int q,l,r,d;
for(int i=1;i<=m;i++){
cin>>q;
if(q==1){
scanf("%d %d %d",&l,&r,&d);
update(l,r,1,1,n,d);
}else{
scanf("%d %d",&l,&r);
printf("%lld\n",query(l,r,1,1,n));
}
}
return 0;
}
























 4823
4823











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








