ArcGIS Pro中的回归分析浅析（上）回归的概念&探索性回归工具使用

2022年，M姐的小伙伴想研究一下空间分析应用，一不小心，小伙伴有点“走火入魔”，在回归分析这条路上，走出了花火，于是，写了一篇学习总结。阅后十分激动，决定分享出来，本内容将分为四个部分依次介绍，分别是：

1）回归概念介绍；

2）探索性回归工具（解释变量的选择）使用；

3）广义线性回归工具(GLR)使用；

4）地理加权回归工具(GWR)使用+小结。

今天我们先分享前两节的内容。回归的概念介绍&探索性回归工具的使用。另外，小伙伴的空间分析应用学习还在进行中，期待她更多的分享~

PART/

01

回归概念介绍

回归分析是最常用的社会科学统计方法。回归用于评估两个或更多要素属性之间的关系。通过回归分析，我们可以对空间关系进行建模、检查和探究；回归分析还可以帮助解释所观测到的空间模式背后的诸多因素，例如为什么有些地区会持续发生年轻人早逝或者糖尿病的发病率比预期要高的情况。

回归分析术语与概念

回归方程：利用一个或多个解释变量对因变量进行最佳预测的数学公式。

在ArcGIS Pro中我们研究的回归可以分为两类，一类是线性回归，另一类是非线性的基于机器学习算法的回归。本章内容我们主要介绍传统的线性回归工具。

ArcGIS Pro中的回归分类

线性回归，用来确定两种或两种以上变量间相互依赖的定量关系。包括普通最小二乘法OLS (Ordinary Least Squares)、广义线性回归GLR(Generalized Linear Regression)、以及地理加权回归GWR(Geographically weighted Regression)等等。

这里以普通最小二乘法为例，介绍一下其公式。公式有助于我们更好地理解工具中的参数以及解释结果。

普通最小二乘法

y 是因变量，用来表示我们试图预测、理解和建模的现象，也就是被分析的对象

X 是解释变量，也叫做自变量，也就是用来解释因变量的变量。解释变量可以有多个

β 是回归系数，用来表示x和y之间的关系强度和类型。

这个关系既可以是正相关，也可以是负相关，更有甚者是没有什么显著关系的（这种情况下就要考虑该解释变量是否有存在的必要了）。

这里举一个回归系数的例子，比如我们对入室盗窃进行建模，并计算得出收入变量的系数为负值，这意味着随着人们收入的上升，住宅入室盗窃的数量下降。

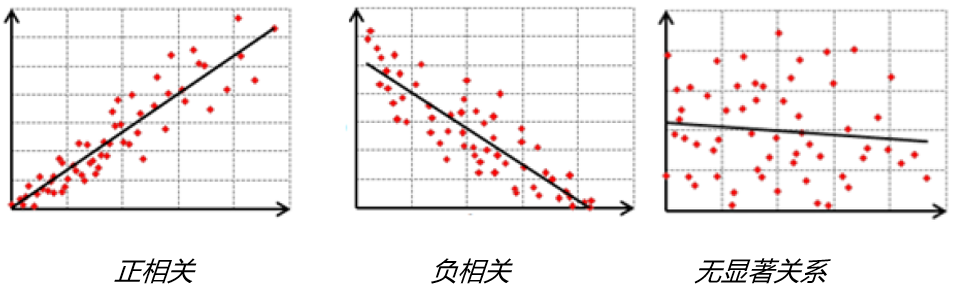
X轴为解释变量，y轴为因变量

还有一个值β0 是指回归截距，它表示所有解释变量均为0时因变量的预期值。

ε是随机误差项，是因变量无法解释的部分。

如下图所示，绿色点为因变量观测值，也就是实际值，红色点是构建了上述方程之后计算得到的预测值，预测值与观测值之间的差值就是随机误差。

回归方程中的预测值与观测值

线性回归经常会遇到两个问题，一是解释变量多重共线性，或者说冗余，这会导致模型估计失真或难以估计准确，我们希望因变量与不同的解释变量之间存在线性关系，同时不同的解释变量彼此之间不是线性相关的。

二是模型过拟合，过拟合是指为了得到一致假设而使假设变得过度严格。一般是由于强化了太多的局部特征，而导致模型的适应性（泛化）太弱。

过拟合问题描述

这是我们在构建线性回归模型时，需要注意的。

广义线性回归GLR(generalized linear regression)

普通最小二乘法 (OLS) 是所有回归方法中最著名的方法。而且，它也是所有空间回归分析的起点。

ArcGIS Pro中提供了普通最小二乘法工具，可以直接使用。当然我们更建议使用新的包含了OLS算法的工具--广义线性回归 (GLR)工具， 可生成预测，或对因变量与一组解释变量的关系进行建模。此工具可用于拟合连续 (OLS)、二进制（逻辑）和计数（泊松）模型。

广义线性回归是一种回归方法用来估计和建模变量之间的线性关系然后用这个模型来产生预测。也就是为变量之间建立线性关系。它是一种全局回归方法，也就是说整个的因变量都可以使用一个公式来表示。

地理加权回归GWR(Geographically weighted Regression)

地理加权回归是一种基于空间变化关系建模的局部线性回归方法。通过对数据集中的每一个要素拟合回归方程，GWR 可以评估想要了解或预测的变量或过程，单个要素的拟合模型范围是邻域内的要素。

实验准备

很多同学在使用回归系列工具时，都会遇到下列问题：

1.我的解释变量是不是足够多？

2.我的模型合适吗？能说明解释变量与因变量之间的相关关系吗？

3.我的模型准确吗？有没有更加准确的回归模型？

4.模型构建完成后，又该从哪些角度解释模型的合理性呢？

我们以一个应用为例，来探索ArcGIS Pro中线性回归工具的使用方法，并分析模型性能指标，得到更合理的结论。

实验数据：俄勒冈州波特兰市部分地区的911紧急呼叫数据

工程及数据下载地址：

https://pan.baidu.com/s/1Ls6f4akAa7k43iiBwjdkpg?pwd=friv

提取码：friv

在ArcGIS Pro中打开该工程，并观察名为Regression Analysis地图

地图视图中加载了4个图层，分别是Data911calls 点图层，ObsData911Calls面图层，Frame面图层，BackGround高程图层。

ArcGIS Pro中加载实验数据

其中Frame和BackGround数据可以当做背景数据，不参与分析。

Data911calls 点图层则标识了一段时间内拨打911电话的信息，共计有2152起。

为了更好地分析911电话与社区中其他解释变量的关系，这里我们对Data911calls 点图层做了处理，将其汇总到人口普查区域面区域中，也就是ObsData911Calls面图层中，打开该图层属性表，有一个Calls字段就表示各区的911电话统计个数。这就是我们研究的因变量。

同时还可以看到这个属性表中包含了其他的字段，例如低教育程度人数（LowEd），失业率（Unemploy）等等，我们可以将收集到的这些字段作为解释变量的候选项，当然我们不能将全部的字段都作为解释变量，在统计学中，在模型的拟合度相同的情况下，解释变量更少的模型更好。

PART/

02

探索性回归工具（解释变量的选择）使用

那究竟哪些变量能解释911电话的分布呢？

这里我们可以有两种方法

一种是使用散点图矩阵。

使用数据→创建图表→散点图矩阵构建(数字字段中必须包含要研究的因变量Calls)。

研究图层散点图矩阵

图上可以看出各个变量之间是否存在线性关系，但是不好确定究竟哪些变量要参与运算，同时还能保证变量不冗余。

另一种是使用探索性回归工具。这里我们更推荐使用这种方法。

探索性回归工具是对输入的候选解释变量的所有可能组合进行评估，以便根据用户所指定的指标来查找能够最好地对因变量做出解释的OLS模型（OLS模型是GLR中的一种最常见的情况）。换句话说探索性回归工具能够帮助我们找到合适的解释变量。

它的实现原理可以简单看做是在解释变量中选择变量进行组合，比较拟合结果，判断哪些方案或者说哪些变量出现在公式中更合理，拟合度更高。比如我们有12个变量，可以是1个解释变量、2个解释变量、3个、4个…依次进行组合并计算其拟合程度等模型信息，找到最合适的。

探索性回归工具

来看一下工具的参数：

输入要素：ObsData911Calls面要素

因变量：这里我们选择要解释的变量，也就是Y值为calls，911电话呼叫次数

候选解释变量：选择你认为的可能跟因变量有线性关系的变量，在这里我选择了Pop\Jobs\LowEduc\Dst2UrbCen\Renter\Unempoyed\Businesses\NetInLf\ForgnBorn\AlcoholX\MedIncome\CollGrads这12个变量。

像PopDensity这样的变量明显是可以通过其他变量计算得到的，这里就不加入候选解释变量里了（需要保证尽量不包含冗余变量，即不存在多重共线性）。

权重矩阵文件：用于对模型残差进行评估，如果没有提供空间权重矩阵文件，工具将会使用默认参数进行评估，这里我们选择不填。

输出报表文件：输出文本文档。包含任何模型的相关详细信息。

输出结果表：结果作为表格输出，表格中包含系数 p 值和 VIF 值以及边界内所有模型的解释变量和诊断信息。

搜索条件：这是工具的核心参数，我们将在GLR工具中对这些参数进行解释。这里参数保持默认。

运行工具。

结果解读：

可以在历史工具中找到其详细信息，查看其消息，也可以在独立表中查看结果文档。

运行结果

内容比较多，文档中会列出不同组合，包括12选1、12选2、12选3至12选5这几种情况的不同组合，并对其进行评估，将AdjR2、AICc、JB、K(BP)、VIF、SA这几个参数均在合格范围内的模型称为通过模型。

这里我们选4/12来简单解释一下。

在通过模型中列出了13种组合，并按照AdjR2的值进行降序排列。

也就是说如果是在12个变量中选择4个解释变量来预测因变量，最高可以解释83. 1%的因变量，或者说模型预测的精确度最高到83. 1%。

在这个模型中，使用了Pop, Jobs, LowEduc, Dst2UrbCen这4个解释变量。

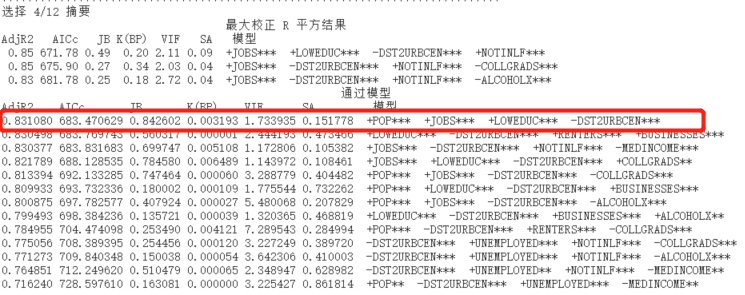
12选4组合

当然你也可以使用5/12的组合来挑选解释变量，它的精确程度更高。

12选5组合

显然5/12虽然比4/12精确度更高，但是精确程度差别不太大，从83.1%上升到了85.8%，要求的变量个数更多也意味着我们需要获取更多的属性值（最重要的是在5/12中的NotInLF变量找不到相关的描述）。

再来看多重共线性汇总的内容：

多重共线性汇总

其中变量POP与Alcoholx\CollGrads\NotInLF是有线性关系的，也就是说当变量POP发生变化，Alcoholx\CollGrads\NotInLF也是会发生变化的。在线性方程中，尽量不要把关联性大的变量都选中。

结论：我们可以选择Pop, Jobs, LowEduc, Dst2UrbCen这4个解释变量或者是Jobs, LowEduc, Dst2UrbCen，Businesses和NotInLF这5个解释变量来做广义线性回归。这里我们选择Pop, Jobs, LowEduc, Dst2UrbCen组合(分别对应人口数量、就业人口数量、文盲人数以及离市中心的距离) 其中人口数量、就业人口数量、文盲人数都很好理解，最后这个离市中心的距离明显是与空间相关的，又该怎么解释呢，我们将会在下一节内容中给出答案。

下节内容预告：

广义线性回归工具(GLR)使用