作者:寒小阳 && 龙心尘
时间:2015年10月。
出处:http://blog.csdn.net/han_xiaoyang/article/details/49123419。
声明:版权所有,转载请注明出处,谢谢。
1、总述
逻辑回归是应用非常广泛的一个分类机器学习算法,它将数据拟合到一个logit函数(或者叫做logistic函数)中,从而能够完成对事件发生的概率进行预测。
2、由来
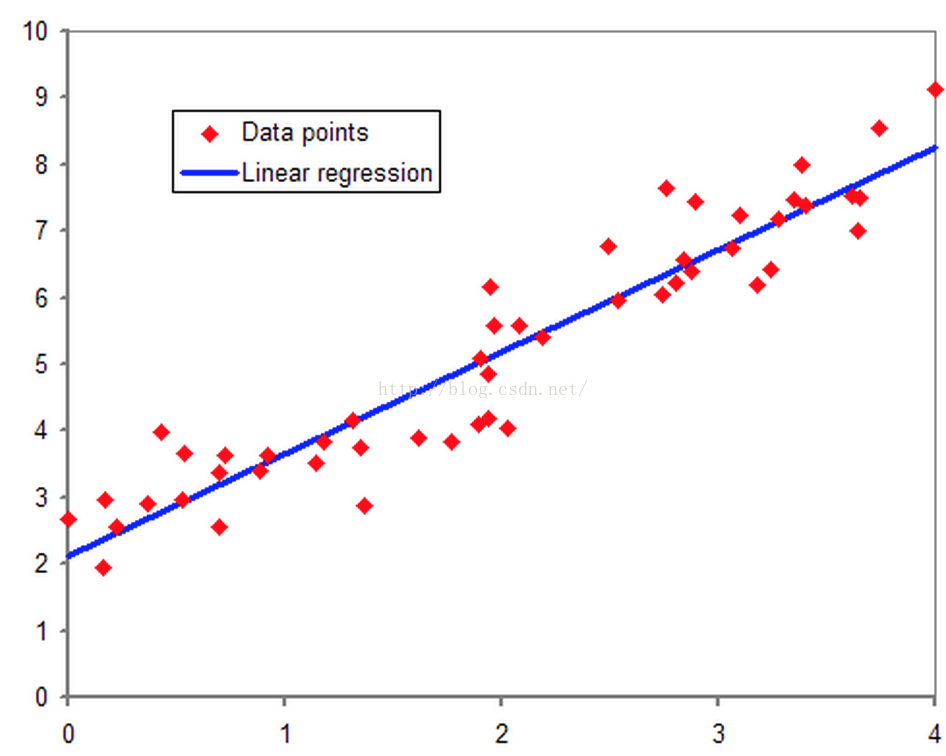
要说逻辑回归,我们得追溯到线性回归,想必大家对线性回归都有一定的了解,即对于多维空间中存在的样本点,我们用特征的线性组合去拟合空间中点的分布和轨迹。如下图所示:
线性回归能对连续值结果进行预测,而现实生活中常见的另外一类问题是,分类问题。最简单的情况是是与否的二分类问题。比如说医生需要判断病人是否生病,银行要判断一个人的信用程度是否达到可以给他发信用卡的程度,邮件收件箱要自动对邮件分类为正常邮件和垃圾邮件等等。
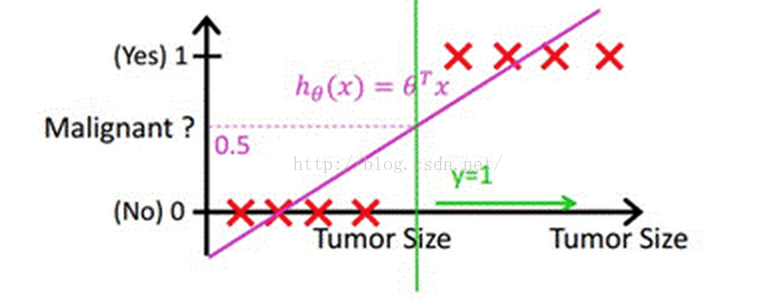
当然,我们最直接的想法是,既然能够用线性回归预测出连续值结果,那根据结果设定一个阈值是不是就可以解决这个问题了呢?事实是,对于很标准的情况,确实可以的,这里我们套用Andrew Ng老师的课件中的例子,下图中X为数据点肿瘤的大小,Y为观测结果是否是恶性肿瘤。通过构建线性回归模型,如hθ(x)所示,构建线性回归模型后,我们设定一个阈值0.5,预测hθ(x)≥0.5的这些点为恶性肿瘤,而hθ(x)<0.5为良性肿瘤。
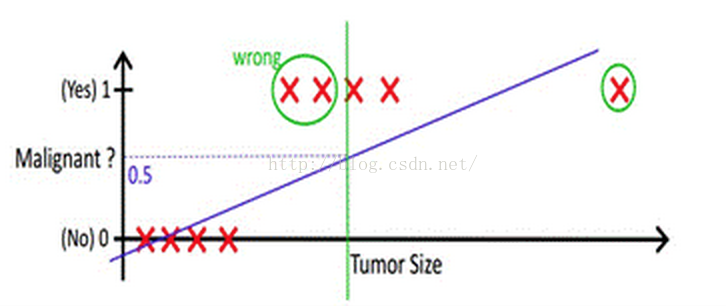
但很多实际的情况下,我们需要学习的分类数据并没有这么精准,比如说上述例子中突然有一个不按套路出牌的数据点出现,如下图所示:
你看,现在你再设定0.5,这个判定阈值就失效了,而现实生活的分类问题的数据,会比例子中这个更为复杂,而这个时候我们借助于线性回归+阈值的方式,已经很难完成一个鲁棒性很好的分类器了。
在这样的场景下,逻辑回归就诞生了。它的核心思想是,如果线性回归的结果输出是一个连续值,而值的范围是无法限定的,那我们有没有办法把这个结果值映射为可以帮助我们判断的结果呢。而如果输出结果是 (0,1) 的一个概率值,这个问题就很清楚了。我们在数学上找了一圈,还真就找着这样一个简单的函数了,就是很神奇的sigmoid函数(如下):
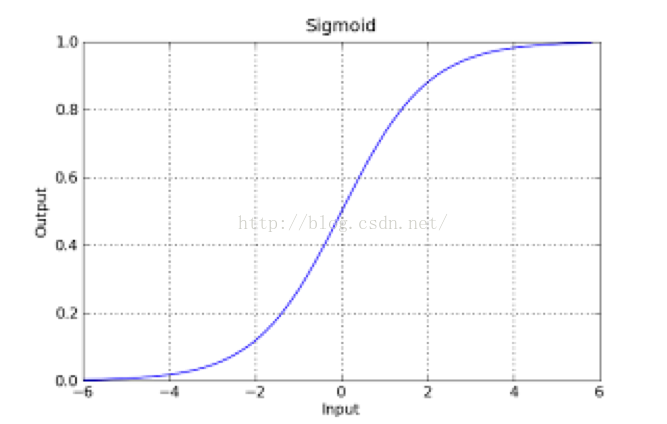
如果把sigmoid函数图像画出来,是如下的样子:
Sigmoid Logistic Function
从函数图上可以看出,函数y=g(z)在z=0的时候取值为1/2,而随着z逐渐变小,函数值趋于0,z逐渐变大的同时函数值逐渐趋于1,而这正是一个概率的范围。
所以我们定义线性回归的预测函数为Y=WTX,那么逻辑回归的输出Y= g(WTX),其中y=g(z)函数正是上述sigmoid函数(或者简单叫做S形函数)。
3、判定边界
我们现在再来看看,为什么逻辑回归能够解决分类问题。这里引入一个概念,叫做判定边界,可以理解为是用以对不同类别的数据分割的边界,边界的两旁应该是不同类别的数据。
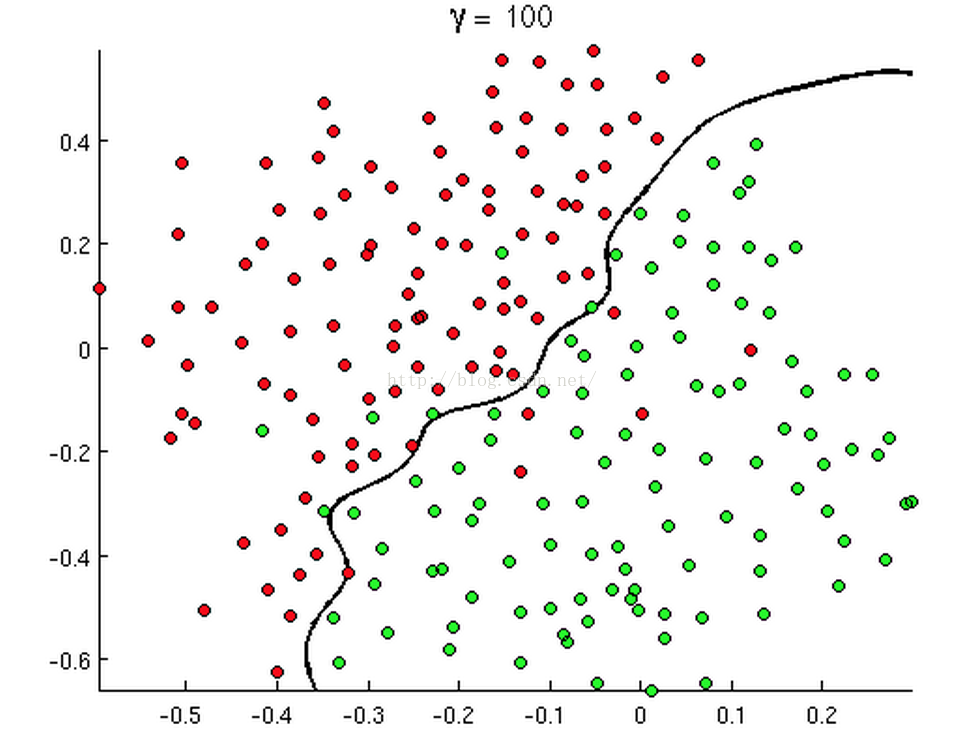
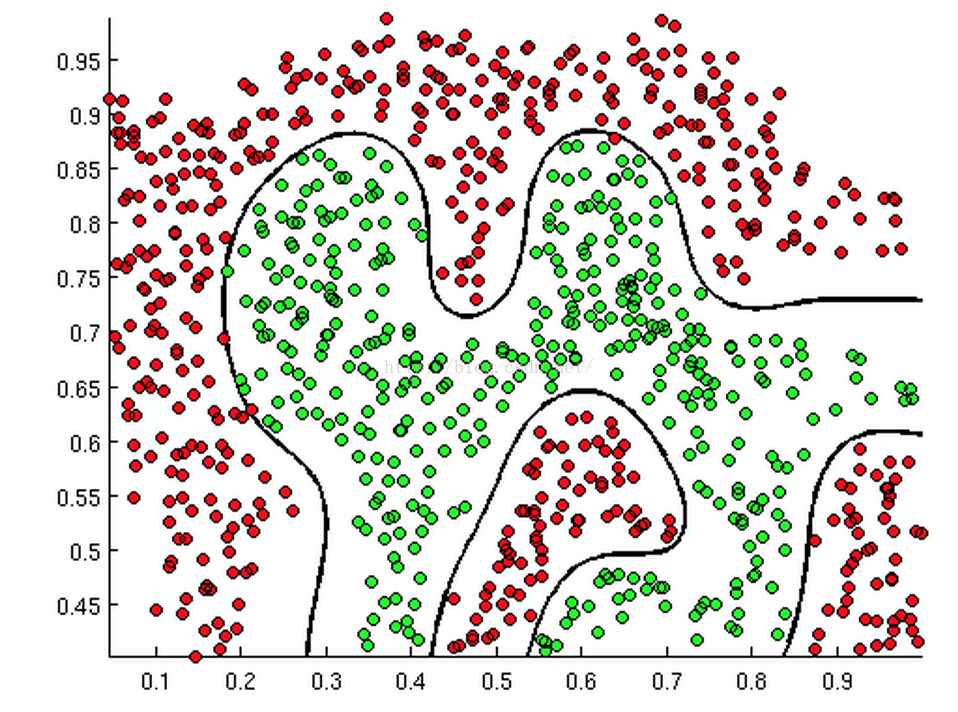
从二维直角坐标系中,举几个例子,大概是如下这个样子:
有时候是这个样子:
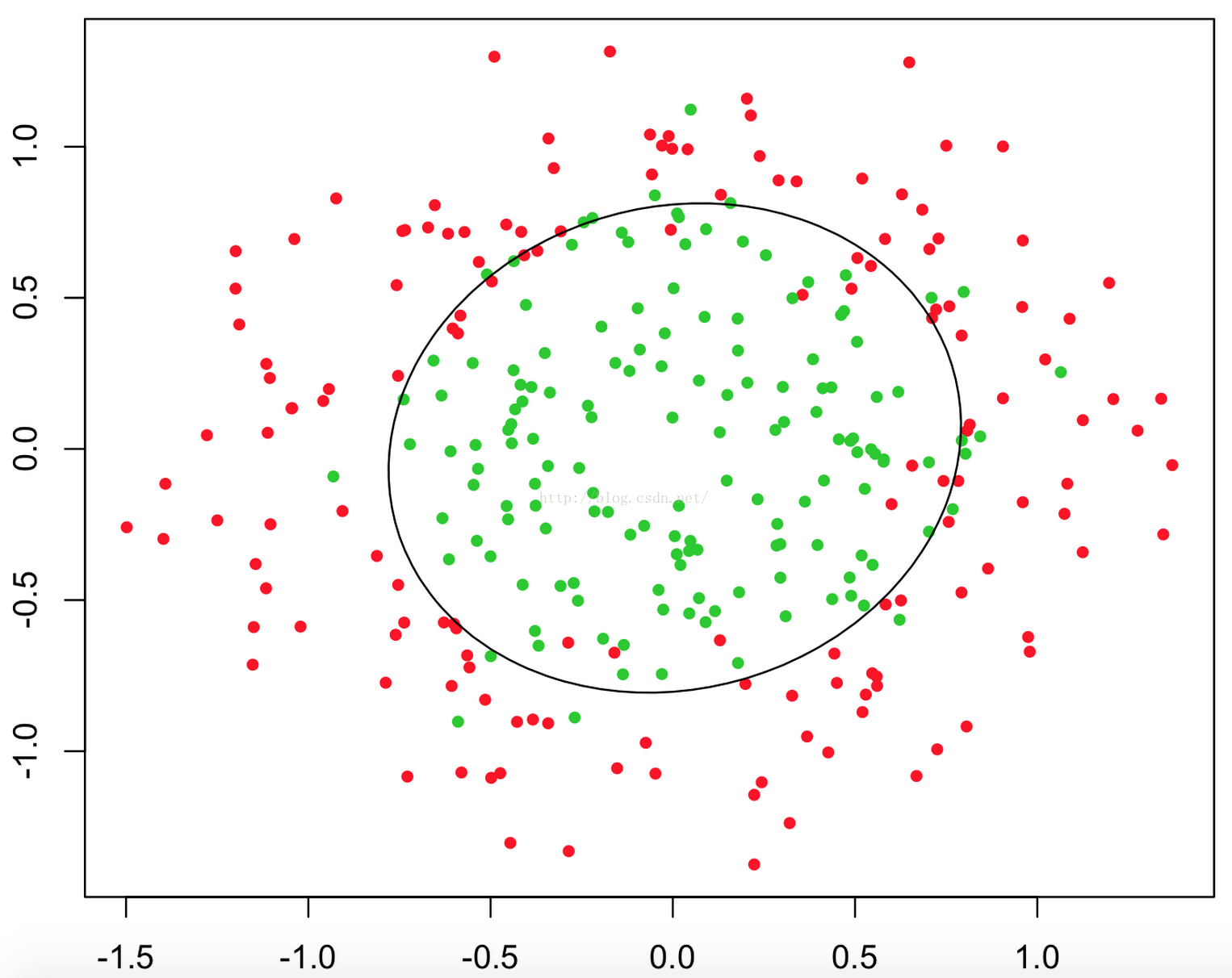
甚至可能是这个样子:
上述三幅图中的红绿样本点为不同类别的样本,而我们划出的线,不管是直线、圆或者是曲线,都能比较好地将图中的两类样本分割开来。这就是我们的判定边界,下面我们来看看,逻辑回归是如何根据样本点获得这些判定边界的。
我们依旧借用Andrew Ng教授的课程中部分例子来讲述这个问题。
回到sigmoid函数,我们发现:
当 g(z)








 逻辑回归是广泛应用的分类算法,通过logit函数预测事件概率。它源于线性回归,解决分类问题,尤其是二分类问题。通过sigmoid函数将连续值映射到(0,1)概率区间,构建非线性判定边界。文章介绍了逻辑回归的由来、判定边界、代价函数和梯度下降,并提供代码实现和实例分析。"
17425155,1091500,多核计算与程序设计的关键挑战,"['并行计算', '分布式计算', '多线程编程', 'CPU架构', '并发控制']
逻辑回归是广泛应用的分类算法,通过logit函数预测事件概率。它源于线性回归,解决分类问题,尤其是二分类问题。通过sigmoid函数将连续值映射到(0,1)概率区间,构建非线性判定边界。文章介绍了逻辑回归的由来、判定边界、代价函数和梯度下降,并提供代码实现和实例分析。"
17425155,1091500,多核计算与程序设计的关键挑战,"['并行计算', '分布式计算', '多线程编程', 'CPU架构', '并发控制']
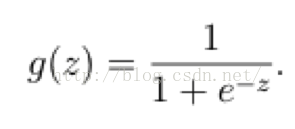
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 847
847

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








