课程作业原地址:CS231n Assignment 1
作业及整理:@张铮 && @郭承坤 && @寒小阳
时间:2018年2月。
出处:http://blog.csdn.net/han_xiaoyang/article/details/79278917
问题描述:使用IPython Notebook(现版本为jupyter notebook,如果安装anaconda完整版会内置),在ConvolutionalNetworks.ipynb文件中,你将实现几个卷积神经网络中常用的新层。使用CIFAR-10数据,训练出一个深度较浅的卷积神经网络,最后尽你所能训练出一个最佳的神经网络。
任务
实现卷积神经网络卷积层的前向计算与反向传导
实现卷积神经网络池化层的前向计算与反向传导
卷积层与池化层的加速
卷积神经网络结构
常规神经网络的输入是一个向量,经一系列隐层的转换后,全连接输出。在分类问题中,它输出的值被看做是不同类别的评分值。
神经网络的输入可不可以是图片呢?
常规神经网络对于大尺寸图像效果不尽人意。图片的像素点过多,处理起来极为复杂。因此在处理图片的过程中较为合理地降维成为了一个研究方向。于是,在基本神经网络的结构上,衍生出了一种新的神经网络结构,我们称之为卷积神经网络。
下图是一个传统多层卷积神经网络结构:
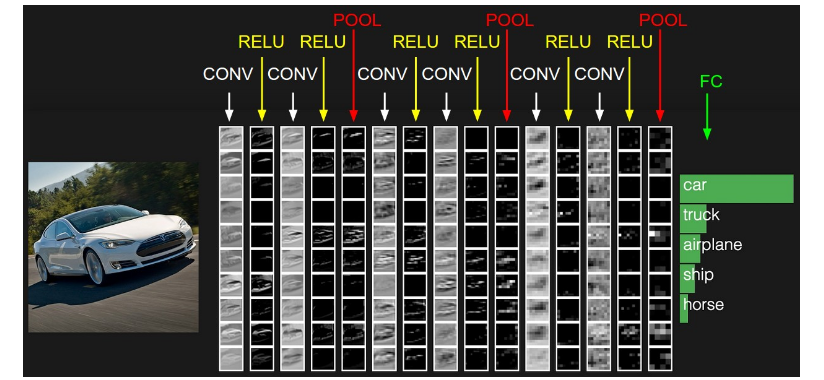
可以看出,上图网络结构开始为“卷积层(CONV),relu层(RELU),池化层(POOL)”C-R-P周期循环,最后由全连接层(FC)输出结果。
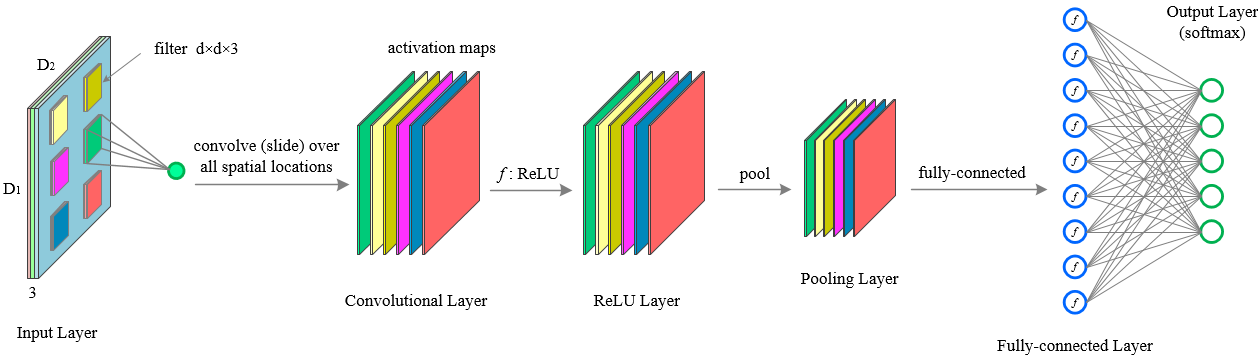
注:实际应用的过程中常常不限于C-R-P循环,也有可能是C-C-R-P等等
设激活函数为 fsigmoid(−) f s i g m o i d ( − ) ,池化操作为 pool(−) p o o l ( − ) ,x代表输入的图像像素矩阵,w代表过滤层(卷积核),b代表偏置。C-R-P周期则有下面的计算公式:
卷积神经网络的理解比较困难,为了更好地理解,我们先讲解过程再讨论实际应用。
卷积层的朴素(无加速算法)实现与理解
(在实际应用过程中,一般使用加速处理的卷积层,这里表现的是原始版本)
卷积层元素
下图是卷积层的元素:输入图片与过滤参数。
输入图片(image):输入层(Input Layer)有3个深度(D1,D2,D3,通常代表图片的三个通道RGB)。我可以将每个深度独立出来,看成三幅图片。图片的大小为32*32。
过滤参数(filter):过滤器有很多称呼,如“卷积核”、“过滤层”或者“特征检测器”。不要被名词坑了。过滤器也有3个深度(D1,D2,D3),就是与输入图片的深度进行一一对应,方便乘积操作。过滤器窗口一般比输入图片窗口小。
卷积层的前向计算
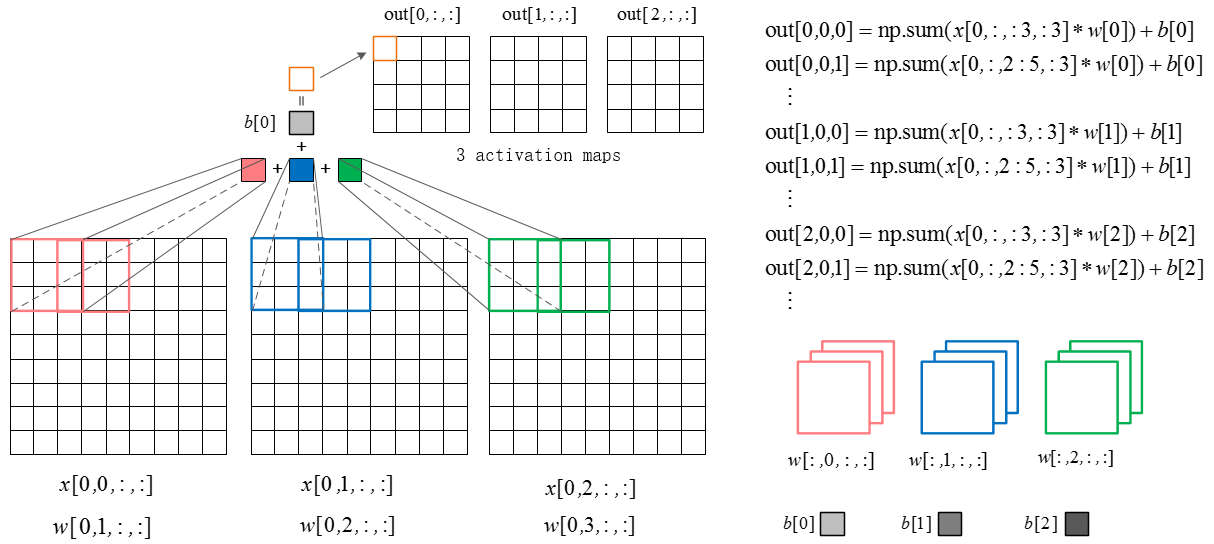
下图是卷积层的具体实现方法。
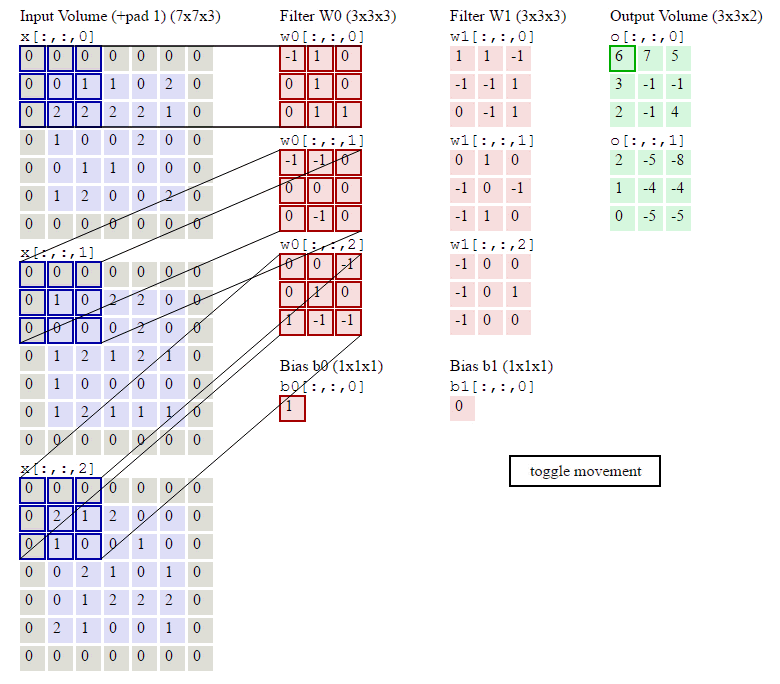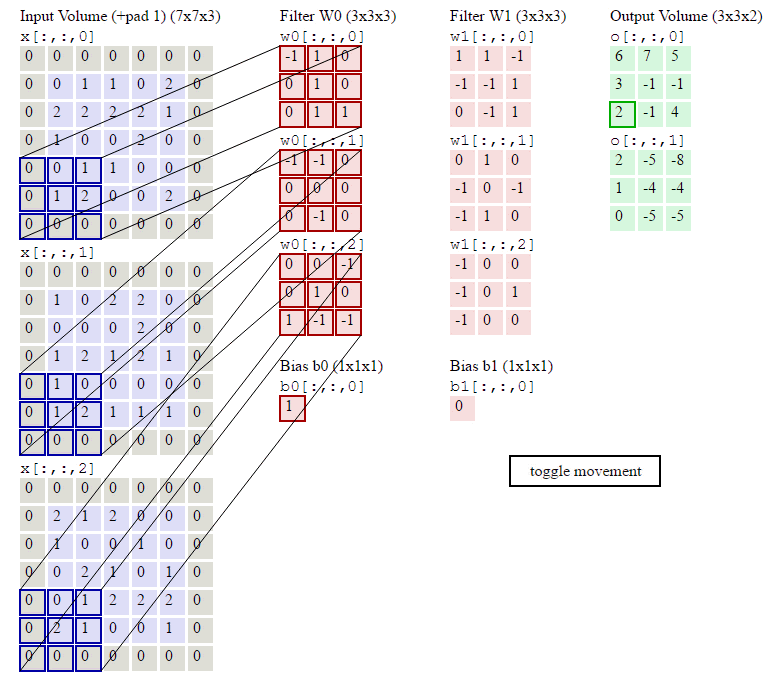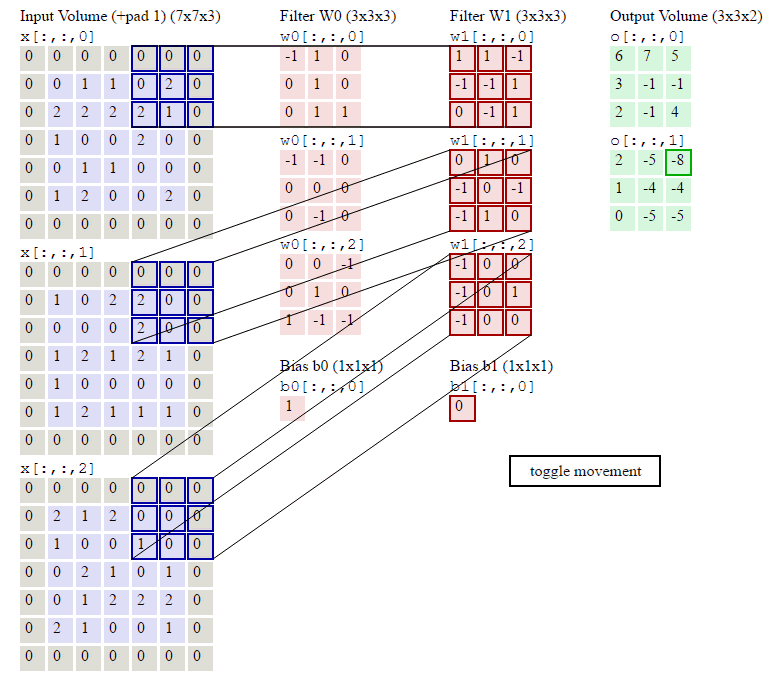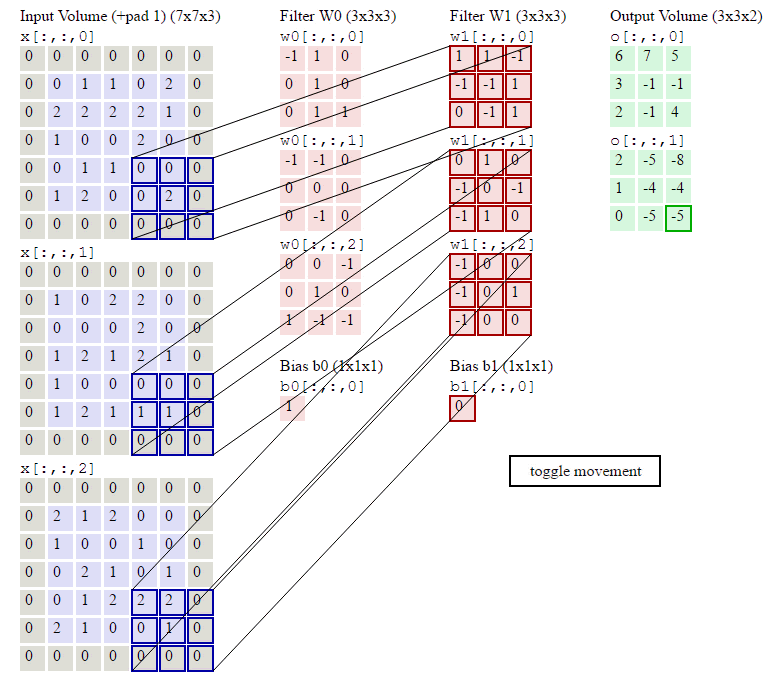
x代表图片image矩阵,w代表过滤层矩阵。各个过滤器分别与image的一部分进行点积,用点积结果排列成结果,这就是卷积过程。下面的动图就是卷积过程。
上图中我们看到每次窗口移动2格。这2格就是每次卷积的移动步长。
我们看到原来的图片在周围填充了一圈0。填充0的宽度即为每次卷积的填充宽度padding(上图的填充宽度就是1)
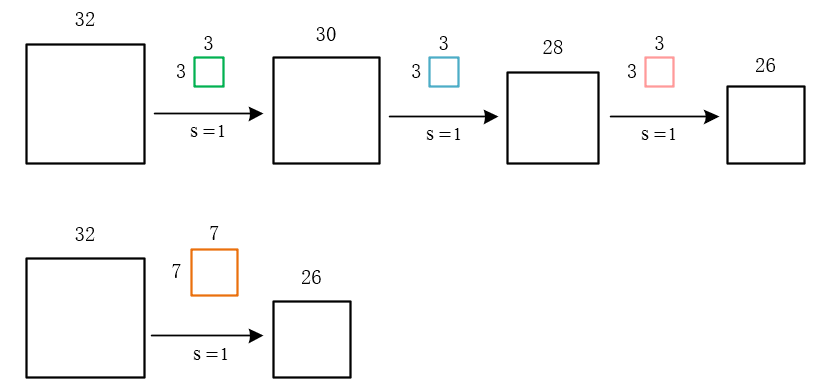
移动步长很好理解,但为什么要填充呢?假设我们不填充。如下图:
会发现每次卷积之后都会有维度降低。浅层卷积网络可能没有什么问题。但是深层卷积可能在网络没到最后的时候维度即降为0。
这显然不是我们所希望的。
当然,如果有意愿用卷积计算去降维也可以,不过我们更喜欢用池化层的池化操作降维。为甚?因为卷基层和池化层各有分工!我们先来了解卷积层的作用。
卷积层正向卷积过程代码实现
def conv_forward_naive(x, w, b, conv_param):
"""
A naive implementation of the forward pass for a convolutional layer.
The input consists of N data points, each with C channels, height H and
width W. We convolve each input with F different filters, where each filter
spans all C channels and has height HH and width HH.
Input:
- x: Input data of shape (N, C, H, W)
- w: Filter weights of shape (F, C, HH, WW)
- b: Biases, of shape (F,)
- conv_param: A dictionary with the following keys:
- 'stride': The number of pixels between adjacent receptive fields in the
horizontal and vertical directions.
- 'pad': The number of p







 本文是斯坦福计算机视觉与深度学习课程CS231n的作业分享,重点讨论卷积神经网络(CNN)的实现与理解,包括卷积层、池化层的前向计算与反向传播,以及空间批量正则化。通过CIFAR-10数据集训练CNN模型,探讨卷积层的作用,如像素信息整合,并介绍神经网络的编写建议。
本文是斯坦福计算机视觉与深度学习课程CS231n的作业分享,重点讨论卷积神经网络(CNN)的实现与理解,包括卷积层、池化层的前向计算与反向传播,以及空间批量正则化。通过CIFAR-10数据集训练CNN模型,探讨卷积层的作用,如像素信息整合,并介绍神经网络的编写建议。

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 4101
4101

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








