1 Miller-Rabin算法
1.1 反复平方法求数的幂
希望找出一种有效的方法来计算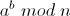
当用二进制来表示b时,采用反复平方法,可以有效的解决这个问题。
设是b的二进制表示。下列过程随着c的值从0到b成倍增长,最终计算出
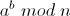
/* a^b mod n */
int mod_exp(int a,int b,int n)
{
int res = 1,p = 1;
for(int i=b;i;i>>=1) p <<= 1;
if(b!=0) p >>= 1;
if(a>n) a %= n;
for(;p;p>>=1)
{
res = (res*res)%n;
if(b&p) res = (res*a)%n;
}
return res;
}
/* (a*b) mod n*/
LL mod_mul(LL a,LL b,LL n)
{
LL t;
x %= n;
for(t=0;b;a=(a<<1)%n,b>>=1)
if (b&1)
t = (t+a)%n;
return t;
}
/* a^b mod n */
LL mod_exp(LL a,LL b,LL n)
{
LL res = 1,temp = a%n;
for(;b;b>>=1,temp=mod_mul(temp,temp,n))
if(b&1)
res = mod_mul(res,temp,n);
return res;
}1.2 费马小定理
根据费马小定理,如果p是素数,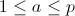
如果我们想知道n是否是素数,我们在中间选取a,看看上面等式是否成立。如果对于数值a等式不成立,那么n是合数。如果有很多的a能够使等式成立,那么我们可以说n 可能是素数,或者伪素数。
在我们检验过程中,有可能我们选取的a都能让等式成立,然而n却是合数。这时等式
被称为Fermat liar。如果我们选取满足下面等式的
那么a也就是对于n的合数判定的Fermat witness。
1.3 Miller-Rabin随机性素数测试方法
输入n>2是一个奇数,该过程测试它是否为素数,s是正整数中随机选取的要进行实验的基值的个数。使用一个辅助过程WITNESS,WITNESS(a,n)为TRUE当且仅当a是一个合数n的“证据”,即,用a来证明n是合数是可能的。测试WITNESS(a,n)是对作为过程伪素数判断的基础(用a = 2)的测试
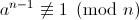
令 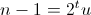
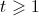
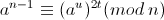
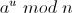
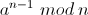
int S;
bool miller_rabin(LL N)
{
if(N==2) return true;
else if(N==1) return false;
//if(n<2 || !(n&1)) return false;
int t = 0; //二进制表示中,n-1共有t位
LL ran,cur,pre,u = N-1;
while((u&1)==0)
t++,u >>= 1; //将n-1表示为(2^t)u
//u为奇数
for(int i=0;i<S;i++) //进行S次判断,选取S=50足够了
{
ran = rand()%(N-1)+1; //选择随机数
pre = mod_exp(ran,u,N); //首先计算a^u mod N
for(int j=0;j<t;j++)
{
cur = mod_mul(pre,pre,N);
if(cur==1 && pre!=1 && pre!=N-1)
return false;
pre = cur;
}
if(pre!=1) return false;
}
return true;
}2. 整数的因子分解
2.1 Pollard_rho启发式方法
对于任意两个正整数x,y,有 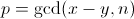
每次可以调用 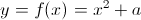
int gcd(int a,int b)
{
if(b==0) return a;
else return gcd(b,a%b);
}
int pollard_rho(int N,int C)
{
int pre,cur,i = 1,k = 2,d;
cur = rand()%(N-1)+1;
pre = cur;
while(true)
{
i++;
cur = (mod_mul(cur,cur,N)+C)&N;
d = gcd(pre-cur,N);
if(1<d && d<N)
return d; //d为一个因子
if(pre==cur)
return N;
if(i==k)
pre = cur,k <<= 1;
}
}在实际进行质因数分解时,需要递归的调用pllard_rho函数,配合miller_rabin函数,判断使得每一个因数都是素数为止。
在调用pollard_rho函数时,需要随机生成随机数C,C的取值范围是在1到N-1之间。
pollard_rho(N,rand()%(N-1)+1); //实际调用pollard_rho函数时,随机选取C的值。
参考资料:







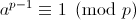
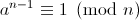
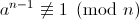














 1669
1669

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








