C++ 判断点是否在旋转矩形内部

流星雨爱编程

已于 2024-11-24 12:41:22 修改

阅读量1k

点赞数 26

分类专栏： #数据结构和算法文章标签：平面 c++ 开发语言算法

于 2024-11-24 12:15:18 首次发布

本文链接：https://blog.csdn.net/haokan123456789/article/details/144003831

版权

#数据结构和算法专栏收录该内容

11 篇文章

订阅专栏

1.问题

在C++中，判断一个点是否在旋转矩形（也称为任意四边形）内部可以通过多种方法实现。一种常见的方法是使用射线法或者多边形的顶点坐标和边的向量来确定。

2.向量

向量具有大小和方向。
共线向量：两个平行的向量为共线向量。

2.1.叉积 Cross Product

2.2.点积 Dot Product

2.3.实际运用

3.向量叉乘方法

以下是使用顶点坐标和向量叉乘来判断点是否在旋转矩形内部的步骤：

1. 定义旋转矩形：

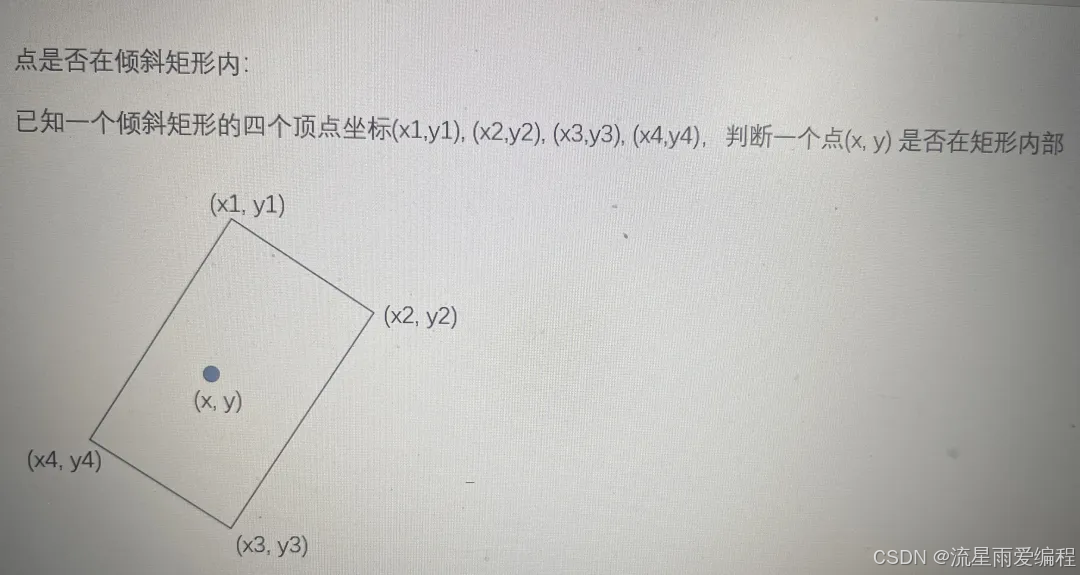
假设旋转矩形由四个顶点 A(x1, y1)，B(x2, y2)，C(x3, y3)，和 D(x4, y4) 定义。

2. 定义点：

设要判断的点为 P(x, y)。

3. 计算向量叉乘：

对于矩形的每一条边，计算由该边和点 ( P ) 形成的向量叉乘。如果点 ( P ) 在矩形内部，那么这些叉乘的结果应该保持一致（全部为正或全部为负）。

4. 检查叉乘的符号：

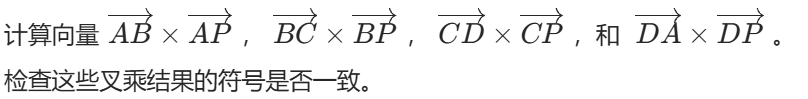
5. 编写代码：

以下是C++代码示例，用于判断点是否在旋转矩形内部：


#include <iostream>

struct Point {
    double x, y;
};

// 计算向量叉乘，返回z分量
double cross(const Point& o, const Point& a, const Point& b) {
    return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
}

// 判断点是否在旋转矩形内部
bool isPointInside(const Point& A, const Point& B, const Point& C, const Point& D, const Point& P) {
    double d1 = cross(P, A, B);
    double d2 = cross(P, B, C);
    double d3 = cross(P, C, D);
    double d4 = cross(P, D, A);

    // 检查叉乘的符号是否一致
    if ((d1 > 0 && d2 > 0 && d3 > 0 && d4 > 0) ||
        (d1 < 0 && d2 < 0 && d3 < 0 && d4 < 0)) {
        return true;
    }
    return false;
}

int main() {
    Point A = {1, 1}, B = {5, 1}, C = {5, 5}, D = {1, 5}, P = {3, 3};
    bool result = isPointInside(A, B, C, D, P);
    std::cout << "The point is " << (result ? "inside" : "outside") << " the rectangle." << std::endl;
    return 0;
}

请注意，这种方法假设矩形的顶点按顺序排列（即不自相交）。如果矩形的顶点不是按顺序排列的，或者矩形可能自相交，那么需要更复杂的算法来处理这些情况。此外，这种方法不适用于凹多边形，因为叉乘不能正确处理凹多边形内部的点。对于凹多边形，可能需要使用多边形的凸包或者更高级的几何算法。

4.解释

检查叉乘结果的符号是否一致来判断点是否在旋转矩形内部的原理基于向量叉乘的几何意义和多边形的几何特性。以下是详细的解释：

向量叉乘的几何意义

向量叉乘的结果是一个垂直于两个原始向量的向量，其大小等于两个向量构成的平行四边形的面积，方向遵循右手定则。当两个向量平行时，叉乘结果为零。

叉乘与多边形内部的关系

符号一致性

如果点 ( P ) 在四边形外部，那么它与四边形的某些边形成的叉乘结果将具有不同的符号。这是因为点 ( P ) 会在不同的边上形成不同方向的“突出”部分，导致叉乘结果的符号变化。
如果点 ( P ) 在四边形内部，那么它与四边形的每条边形成的叉乘结果将具有相同的符号。这是因为点 ( P ) 相对于四边形的所有边都位于同一侧，因此所有叉乘结果的方向一致。

符号不一致的情况