一、熵 entropy
表示随机变量不确定性,熵越大,不确定性越大。

1.联合熵
两个随机变量X,Y的联合分布,可以形成
联合熵Joint Entropy,用H(X,Y)

2.条件熵:
H(Y|X) = H(X,Y) - H(X)

根据互信息定义展开得到
H(Y|X) = H(Y) - I(X,Y)
3. 对偶式
H(X|Y)= H(X,Y) - H(Y)
H(X|Y)= H(X) - I(X,Y)
4.交叉熵
相对熵,又称互熵,交叉熵,鉴别信息,Kullback熵,Kullback-Leible散度等
设p(x)、q(x)是X中取值的两个概率分布,则p对q的
相对熵是

两点说明:
1) 在一定程度上,相对熵可以度量两个随机变量的“距离”
2) 一般的,D(p||q) ≠D(q||p)
5.互信息:
两个随机变量X,Y的互信息,定义为X,Y的联合分布和独立分布乘积的相对熵。

I(X,Y)=H(Y) – H(Y|X)
I(X,Y)= H(X) + H(Y) - H(X,Y)
证明:H(Y) –I(X,Y)=H(Y|X)

记忆图:

二、决策树
1.介绍:
决策树是一种树型结构,其中每个内部结点表示在一个属性上的测试,每个分支代表一个测试输出,每个叶结点代表一种类别。
1) 决策树学习是以实例为基础的归纳学习。
2) 决策树学习采用的是自顶向下的递归方法,
其基本思想是以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵值为零,此时每个叶节点中的实例都属于同一类。它属于有监督学习。可以 从一类无序、无规则的事物(概念)中推理出决策树表示的分类规则。
建立决策树的关键,即在当前状态下选择哪个属性作为分类依据。根据不同的目标函数,建立决策树主要有一下三种算法。
ID3(信息增益)
C4.5(信息增益率)
CART(gini指数)
2.建树分叉依据
1) ID3
ID3是以信息增益为选择分类特征的依据,由于当特征取值越丰富,信息增益越大,所以ID3会偏向于选择属性值多的特征。
1)信息增益
(当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时,所对应的熵和条件熵分别
称为经验熵和经验条件熵。)
信息增益表示得知特征A的信息而使得类X的信息的不确定性减少的程度。
定义:特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D
的经验条件熵H(D|A)之差,即:
g(D,A)=H(D) – H(D|A)
显然,这即为训练数据集D和特征A的互信息。
设训练数据集为D,|D|表示其容量,即样本个数。设有K个类Ck,k=1,2,…,K,|Ck|为属于类Ck的样本个数。Σk|Ck|=|D|。设特征A有n个不同的取值{a1,a2…an},根据特征A的取值将D划分为n个子集D1,D2,…Dn,|Di|为Di的样本个数,Σi|Di|=D。记子集Di中属于类Ck的样本的集合为Dik,|Dik|为Dik的样本个数。
计算数据集D的经验熵
![]()
计算特征A对数据集D的经验条件熵H(D|A)

计算信息增益:g(D,A)=H(D) – H(D|A)
一个属性的信息增益越大,表明属性对样本的熵减少的能力更强,这个属性使得数据由不确定性变成确定性的能力越强。
如果是取值更多的属性,更容易使得数据更“纯” ,其信息增益更大,决策树会首先挑选这个属性作为树的顶点。结果训练出来的形状是一棵庞大且深度很浅的树,这样的划分是极为不合理的。
2)C4.5
信息增益率:gr(D,A) = g(D,A) / H(A)
3)CART
基尼指数:

4.考察基尼指数的图像、熵、分类误差率三者之间的关系

将f(x)=-lnx在x0=1处一阶展开,忽略高阶无穷小,得到f(x)≈1-x

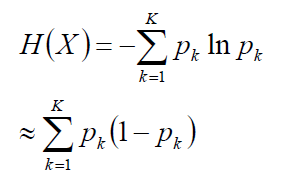
三、解决过拟合问题
1.剪枝
三种决策树的剪枝过程算法相同,区别仅是对于当前树的评价标准不同。
信息增益、信息增益率、基尼系数
剪枝总体思路:
由完全树T0开始,剪枝部分结点得到T1,再次剪枝部分结点得到T2…直到仅剩树根的树Tk;
在验证数据集上对这k个树分别评价,选择损失函数最小的树Tα
根据原损失函数:
![]()
叶结点越多,决策树越复杂,损失越大,修正:![]()
当α=0时,未剪枝的决策树损失最小;
当α=+∞时,单根结点的决策树损失最小。
假定当前对以r为根的子树剪枝:
剪枝后,只保留r本身而删掉所有的叶子
考察以r为根的子树:
令剪枝后的损失函数=剪枝前的损失函数,求得a
对于给定的决策树T0:
.计算所有内部节点的剪枝系数;
.查找最小剪枝系数的结点,剪枝得决策树Tk ;
.重复以上步骤,直到决策树Tk只有1个结点;
.得到决策树序列T0T1T2…TK ;
.使用验证样本集选择最优子树。
.使用验证集做最优子树的标准,可以使用评价函数
2.随机森林RF











 本文介绍了熵在衡量随机变量不确定性中的作用,包括联合熵、条件熵、对偶式和互信息。接着深入讨论了决策树的学习过程,如ID3、C4.5和CART算法,以及如何通过信息增益、信息增益率和基尼指数来选择最佳分叉依据。最后,文章提到了解决决策树过拟合问题的剪枝策略。
本文介绍了熵在衡量随机变量不确定性中的作用,包括联合熵、条件熵、对偶式和互信息。接着深入讨论了决策树的学习过程,如ID3、C4.5和CART算法,以及如何通过信息增益、信息增益率和基尼指数来选择最佳分叉依据。最后,文章提到了解决决策树过拟合问题的剪枝策略。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








