算法一:朴素的模式匹配算法
假设我们要从主串s="goodgoogle"找到t="google"这个子串的位置,我们需要下列步骤
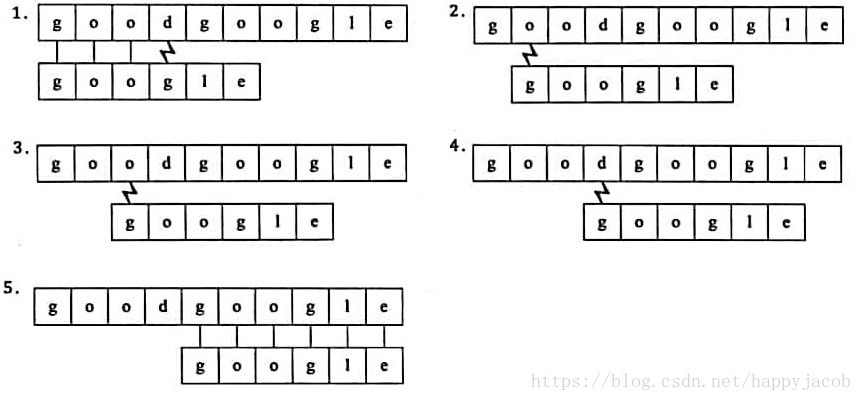
1、主串s的第1位开始,s与t前三个字符都匹配成功,第四个字符不匹配(竖线表示相等,闪电状弯折表示不想等)
2、主串s的第2位开始,匹配失败
3、主串s的第3位开始,匹配失败
4、主串s的第4位开始,匹配失败
5、主串s的第5位开始,s与t,6个字符全部匹配成功
对主串的每一个字符作子串开头,要与匹配的字符串进行匹配。对主串作大循环,每一个字符开头作t长度的小循环,直到匹配成功或者全部遍历完为止。
#include<iostream>
using namespace std;
//返回子串t在主串t中第pos个字符之后的位置;若不存在,函数返回0
//t非空,1≤pos≤s.size()
int Index(string s, string t, int pos=0) //默认为0,默认从第一个元素开始查找
{
int i = pos; //主串t当前下表
int j = 0; //子串t当前下表
while (i<s.size() && j<t.size()) //i小于s长度,j小于t长度,循环继续
{
if (s[i] == t[j])
{
i++;
j++;
}
else //指针退回,重新开始匹配
{
i = i - j + 1; //i退回到上一次匹配首位的下一位
j = 0; //j退回到子串t的首位
}
}
if (j >= t.size())
return i - t.size() + 1; //i - t.size()表示从s[4]开始重复,+1表示该元素为第5个元素
else
return 0;
}
int main()
{
string s = "goodgoogle";
string t = "google";
cout << Index(s, t)<<endl;
return 0;
}复杂度:
最好的情况,比如在"googlegood"中找"google",时间复杂度为O(1)
稍差一点,比如"abcdefgoogle"中找"google",时间复杂度O(n+m),其中n为主串长度,m为子串长度,根据等概率原则,平均(n+m)次查找,时间复杂度为O(n+m)
最坏的情况,每次不成功都发生在串t的最后一个字符,比如子串t="0000000001",9个"0"和一个"1"
主串s="00000000000000000000000000000000000000000000000001",49个"0"和一个"1"
时间复杂度为O((n-m+1)*m)
算法二:KMP模式匹配算法
假设主串s="abcdefgab",t="abcdex"
"abcdex"的首字符"a"与后面的串"bcdex"中任何一个字符都不相等,子串t与主串s的前5个字符分别相等,意味着子串t的首字符"a"不可能与s串的第2位到第5位的字符相等

上面的案例,子串t中没有重复的字符,下面给出一个有重复字符的例子
假设s="abcababca",t="abcabx"
第一步,前5个字符相等,第6个字符不相等,根据前面的经验,t的首字符"a"与t中第二位、第三位字符军部等,不需要判断
子串t中第1位与第4位相等,第2位与第5位相等;主串s中第4位,第5位分别与子串t中第4位,第5位相等,意味着子串的第1位与第2位分别与主串第4位与第5位相等,不需要判断

总结:i值不回溯,j值的变化只与子串有关,取决于t串中的结构中是否有重复的字符串。
我们把t串各个位置的变化定义为一个数组next,next的长度就是t串的长度

举例说明next数组:

#include<iostream>
using namespace std;
//通过计算,返回子串的next数组
void get_next(string t, int *next)
{
int i, j;
i = 1;
j = 0;
next[1] = 0;
while (i<t.size() - 1)
{
if (j == 0 || t[i] == t[j]) //t[i]表示后缀的单个字符,t[j]表示前缀的单个字符
{
i++;
j++;
next[i] = j;
}
else
j = next[j]; //若字符不相同,则j值回溯
}
}
//返回子串t在主串t中第pos个字符之后的位置;若不存在,函数返回0
//s[0]和t[0]应该保存字符串的长度,这里我们随意保存一个字符#
int Index_KMP(string s, string t, int pos = 1) //默认从主串的第一个位置开始查找
{
int i = pos; //i用于表示主串s的当前位置
int j = 1; //j用于表示子串t的当前位置
int next[255]; //定义一个next数组
get_next(t, next); //对串做分析,得到next数组
while (i < s.size() && j < t.size()) //若i小于s的长度且j小于t的长度,循环继续
{
if (j == 0 || s[i] == t[j]) //两字符串相等,或j处于开始位,继续
{
i++;
j++;
}
else //j值退回合适的位置,i值不变
j = next[j];
}
if (j >= t.size())
return i - t.size() + 1;
else
return 0;
}
int main()
{
string s = "#goodgoogle";
string t = "#google";
cout << Index_KMP(s, t) << endl;
return 0;
}时间复杂度:对于get_next来说,t的长度为m,由于只涉及到简单循环,其时间复杂度为O(m);i的值不回溯,主串的长度为n,while循环的时间复杂度为O(n),因此整个代码的数减复杂度为O(n+m)
算法三:KMP模式匹配算法改进
KMP匹配算法还是有缺陷的,比如子串s="aaaabcde",子串t="aaaaax",子串t的next为012345
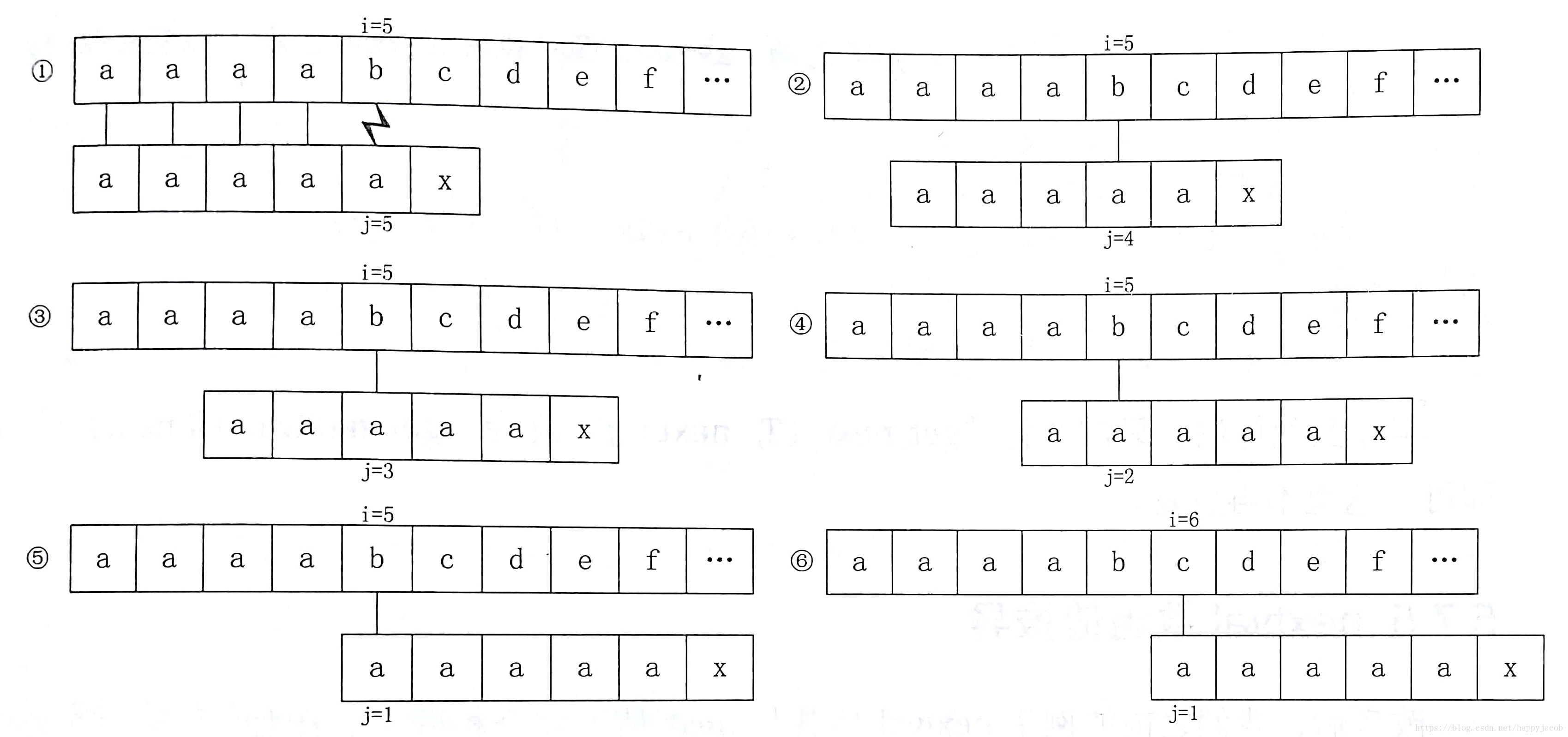
我们发现②③④⑤步骤是多余的。由于子串t中第2、3、4、5个位置上的字符串和守卫上的字符串相等,那么可以用首位next[1]来代替后续与它相等的字符后续的next[j]

取代的数组为nextval[],代码如下
#include<iostream>
using namespace std;
//求模式串t的next函数修正值并存入数组nextval
void get_nextval(string t, int *nextval)
{
int i, j;
i = 1;
j = 0;
nextval[1] = 0;
while (i<t.size() - 1)
{
if (j == 0 || t[i] == t[j]) //T[i]表示后缀的单个字符,T[j]表示前缀的单子字符
{
i++;
j++;
if (t[i] == t[j]) //若当前字符与前缀字符相等
{
nextval[i] = nextval[j];//将前缀字符的nextval值赋值给nextval在i位置上的值
}
else
nextval[i] = j; //当前的j为nextval在i位置上的值
}
else
j = nextval[j]; //不相等,j回溯
}
}
int Index_KMP(string s, string t, int pos = 1)
{
int i = pos;
int j = 1;
int next[255];
get_nextval(t, next);
while (i < s.size() && j < t.size())
{
if (j == 0 || s[i] == t[j])
{
i++;
j++;
}
else
j = next[j];
}
if (j >= t.size())
return i - t.size() + 1;
else
return 0;
}
int main()
{
string s = "Agoodgoogle";
string t = "3google";
cout << Index_KMP(s, t) << endl;
return 0;
}


























 976
976

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








