NLMeans(4)——IPOL Parameter-Free Fast Pixelwise Non-Local Means Denoising 快速算法 精读

Paper & Code:

• Parameter-Free Fast Pixelwise Non-Local Means Denoising  2014-11-19 · Jacques Froment

---

1. NLM的快速算法

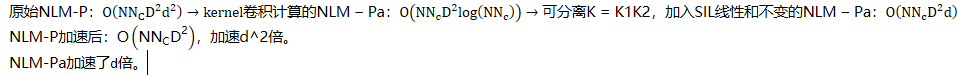
基本的pixelwise-NLM需要的时间复杂度为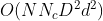：，N为256×256，Nc为通道数。D为搜索半径，d为patch的尺寸。

其时间开销为：

• 主循环：fist pass计算权重 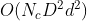，second pass计算聚合，需要。

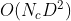• 并行计算：在主循环Level将特定像素x分配给特定线程。可以将执行时间在多个线程上平分。对于普通算法NLM和Fast NLM这个都可以实现的。

1.1 基于积分图的Fast NLM-P

• 降低求patch间欧氏距离的复杂度：积分图。 
  • 积分图的计算在常数时间内实现。算法2
    • 先计算所有的积分图，需要D^2次移动，所以共需要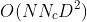操作。
    • Fist Pass中计算patch之间的差，可以用公式计算。
    • NLM的权重w计算与patch的大小无关。fast NLM-P的时间开销在主循环的初始化和Second Pass的开销。。
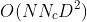    • 缺点：占用大量的内存，需要记录所有的St积分图，需要D^2*N个内存。
• 为了减小内存开销，改变循环的顺序，不需要t去索引积分图St，而是引入一个数组，储存归一化的权重和。内存为2*N。
  • 但是，由于主循环中对估值进行了部分计算，虽然内存优化了，但是不适合并行处理。
• 积分图的缺点：
  • 不允许使用Kernel来加权距离，如高斯核。
  • 当图像尺寸过大，同时Patch的尺寸也较大时，积分图的一些值可能会很大，即使使用双精度类型，最终的计算结果的准确度会下降。
  • 因此这种积分图很难用于实现NLM-Pa。​​​​​​​

1.2 基于FFT的Fast NLM-Pa

• 提出FFT计算NLM-Pa的人，可以考虑任意形状的patch，应用范围更广。通过两个修改可以降低复杂度：
  • （1）避免记录所有的积分图，重新计划循环方式，考虑偏移量。
  • （2）给定t点的patch之间差的加权范数可以用离散卷积的方式来计算。
    • 卷积的时间复杂度为：Nlog(N)。

    • 主循环时间复杂度为O（NNcD2 log（NNc））。所以卷积计算是带有Kernel的NLM的附加开销部分。

​​​​​​​1.3 使用不变线和（SIL）的Fast NLM-Pa

计算patch间的距离可以使用技巧：移动patch的一行或一列时不需要重新计算所有的像素差，而是保留差异。