HDU 2604 Queuing (矩阵快速幂)
ACM
题目地址:HDU 2604 Queuing
题意:
n个人排队,f表示女,m表示男,包含子串‘fmf’和‘fff’的序列为O队列,否则为E队列,有多少个序列为E队列。
分析:
矩阵快速幂入门题。
下面引用巨巨解释:
用f(n)表示n个人满足条件的结果,那么如果最后一个人是m的话,那么前n-1个满足条件即可,就是f(n-1);
如果最后一个是f那么这个还无法推出结果,那么往前再考虑一位:那么后三位可能是:mmf, fmf, mff, fff,其中fff和fmf不满足题意所以我们不考虑,但是如果是
mmf的话那么前n-3可以找满足条件的即:f(n-3);如果是mff的话,再往前考虑一位的话只有mmff满足条件即:f(n-4)
所以f(n)=f(n-1)+f(n-3)+f(n-4),递推会跪,可用矩阵快速幂
构造一个矩阵:
矩阵快速幂和普通的快速幂原理是一样的,如果不懂可以先去补补快速幂。
代码:
/*
* Author: illuz <iilluzen[at]gmail.com>
* Blog: http://blog.csdn.net/hcbbt
* File: 2604.cpp
* Create Date: 2014-08-02 21:20:18
* Descripton: matrix
*/
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#include <cmath>
#include <cstdlib>
#define repf(i,a,b) for(int i=(a);i<=(b);i++)
typedef long long ll;
const int N = 0;
const int SIZE = 4;
int l, MOD;
struct Mat{
ll v[SIZE][SIZE]; // value of matrix
Mat() {
memset(v, 0, sizeof(v));
}
void init(ll _v) {
repf (i, 0, SIZE)
v[i][i] = _v;
}
};
Mat operator * (Mat a, Mat b) {
Mat c;
repf (i, 0, SIZE - 1) {
repf (j, 0, SIZE - 1) {
c.v[i][j] = 0;
repf (k, 0, SIZE - 1) {
c.v[i][j] += (a.v[i][k] * b.v[k][j]) % MOD;
c.v[i][j] %= MOD;
}
}
}
return c;
}
Mat operator ^ (Mat a, ll k) {
Mat c;
c.init(1);
while (k) {
if (k&1) c = a * c;
a = a * a;
k >>= 1;
}
return c;
}
int main() {
Mat a, b, c;
// a
a.v[0][0] = 9;
a.v[1][0] = 6;
a.v[2][0] = 4;
a.v[3][0] = 2;
// b
b.v[0][0] = b.v[0][2] = b.v[0][3] = b.v[1][0] = b.v[2][1] = b.v[3][2] = 1;
while (~scanf("%d%d", &l, &MOD)) {
if (l == 0) {
puts("0");
} else if (l <= 4) {
printf("%lld\n", a.v[4 - l][0] % MOD);
} else {
c = b ^ (l - 4);
c = c * a;
printf("%lld\n", c.v[0][0] % MOD);
}
}
return 0;
}











 本文详细解析了HDU2604Queuing问题,通过矩阵快速幂的方法解决该问题。文章介绍了如何根据题目要求构建递推公式,并给出了具体的矩阵构造方式与快速幂运算实现。
本文详细解析了HDU2604Queuing问题,通过矩阵快速幂的方法解决该问题。文章介绍了如何根据题目要求构建递推公式,并给出了具体的矩阵构造方式与快速幂运算实现。
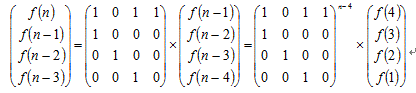

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








