一.harris角点检测的数学原理
对于harris角点检测,其主要思想就是:在图像设计中,用一个高斯窗口沿各个方向(0,360)上移动时,
计算角点量,当角点量大值大于设定的阈值时,就把该窗口的中心像素点提取为角点。
用各个方向上像素差的平方和表示在高斯窗口中的变化量,其函数可以表示为:
这个函数也可以叫自相关函数,(x,y)表示偏移量,(u,v)表示高斯窗口,E(x,y)表示在一个窗口中的平均偏移量函数,
w表示高斯窗口的权重。harris角点检测是把(0,360)各个方向上的平均偏移量都考虑进去了,所以,在一
个高斯窗口中,平均偏移量函数的值是非常多的。那么怎样才能找到角点呢?角点一般认为在两个相互垂直的方向上
都有较大变化的点。所以只要在两个垂直的方向上能找到E(x,y)的极大值,就能够确定该窗口中的角点。那么怎样
才能在两个垂直方向上求极大值?如果用moravec角点检测的方法,求出各个方向上的变化量,太复杂。所以harris提
出了另一种方法,首先要对函数E(x,y)进行一些变换:
也就是说用图像I对(-1,0,1)和(-1,0,1)转置,进行卷积,前面一个就是对x的导数,后面是对y的导数。
先找出E(x,y)取最大值的(x,y),如果该方向E(x,y)有较大的取值,再考虑(x,y)方向的垂直方向。
根据harris角点的定义,harris角点是当(x,y)取两组像话垂直的值时,E(x,y)都有较大值的点。
所以求E(x,y)最大值方向本质上为以下最优化问题
第二个方程表示在一个圆上来求得极大值。
要判断一个点是否为特征点,本质上是要求该点的H矩阵,以及H矩阵的两个特征值。特征值有三种情况:
为什么两个特征值都很大的时候就被认为是角点呢?
首先来理解H矩阵的特征值与角点、平坦区域、边缘之间的关系。二次函数:
本质上是一个椭圆函数。椭圆的扁率和尺寸是由矩阵H的特征值来决定的。椭圆的方向是由H的特征向量决定的。
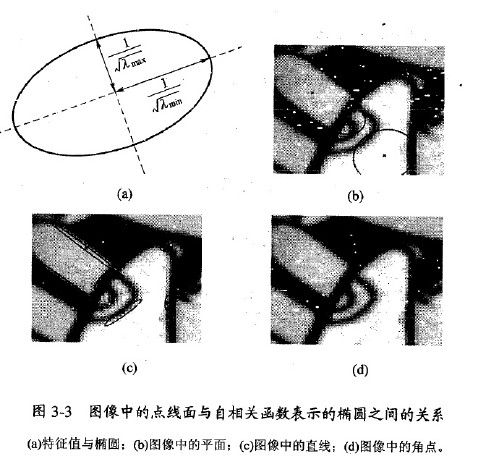
如图:
椭圆函数特征值与图像中的角点,直线,平滑区域的关系如上图。可分为三种情况:
(1)图像上的直线。一个特征值比较大,另外一个特征值比较小,自相关函数在某一个方向上大,在另一个方向上小。
(2)图像中的平滑区域。两个特征值都小,且近似相等。自相关函数值子各个方向上都小。
(3)图像中的角点。两个特征值都比较大,且近似相等,自相关函数在所有方向上都增大。
算出特征值就要就可以判断角点,那怎样计算角点量呢?
角点量计算出来后,就可以用角点量R来和设置的阈值比较,如果比阈值大,就判断为角点。到此,harris角点检测原理结束。
现总结角点检测的步骤:








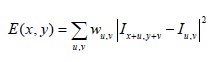



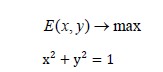


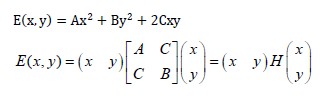
















 2123
2123

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








