图、图的遍历、最小生成树、最短路径

0、图的概念

**图:**是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E)，其中：

• 顶点集合V = {x|x属于某个数据对象集}是有穷非空集合；
• 边的集合E = {(x,y)|x,y属于V}或者E = {|x,y属于V && Path(x, y)}是顶点间关系的有穷集合。

(x, y)表示x到y的一条双向通路，即(x, y)是无方向的；Path表示从x到y的一条单向通路，即Path 是有方向的。
**顶点和边：**图中结点称为顶点，第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边， 图中的第k条边记作ek，ek = (vi，vj)或<vi，vj>。
**有向图和无向图：**在有向图中，顶点对<x,y>是有序的，顶点对<x,y>称为顶点x到顶点y的一条边(弧)，<x,y>和<y,x>是两条不同的边，比如下图G3和G4为有向图。在无向图中，顶点对(x, y)是无序的，顶点对(x,y) 称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x, y)和(y,x)是同一条边，比如下图G1和G2为 无向图。注意：无向边(x, y)等于有向边<x,y>和<y,x>。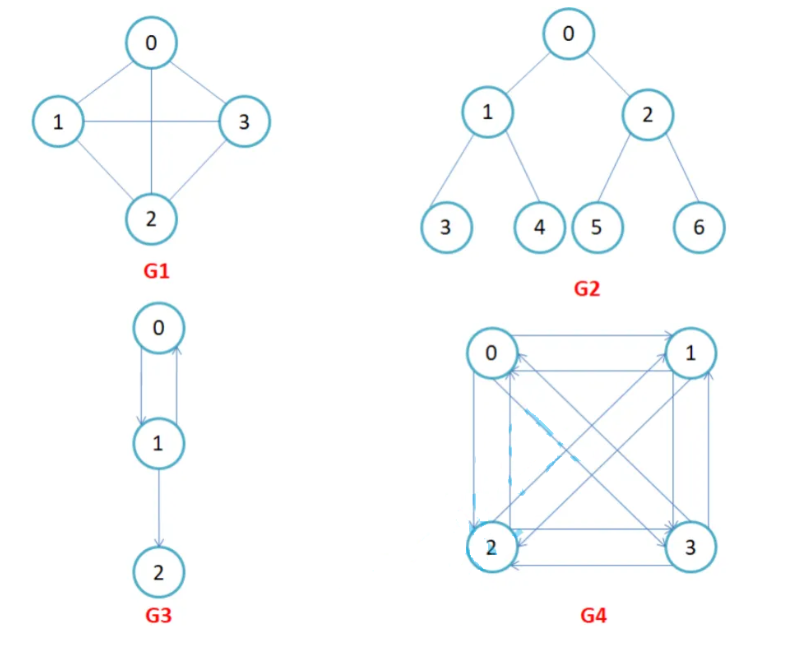

完全图：在有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边，则称此图为无向完全图，比如上图G1；在n个顶点的有向图中，若有n * (n-1)条边，即任意两个顶点之间有且仅有方向相反的边，则称此图为有向完全图，比如上图G4。
邻接顶点**：在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点**，并称边(u,v)依附于顶点u和v；在有向图G中，若是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边与 顶点u和顶点v相关联。
顶点的度：顶点v的度是指与它相关联的边的条数，记作deg(v)。在有向图中，顶点的度等于该顶点的入度与 出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v);顶点v的出度是以v为起始点的有向 边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。注意：对于无向图，顶点的度等于该顶 点的入度和出度，即dev(v) = indev(v) = outdev(v)。
路径：在图G = (V， E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶点序列为从 顶点vi到顶点vj的路径。
路径长度：对于不带权的图，一条路径的路径长度是指该路径上的边的条数；对于带权的图，一条路径的路 径长度是指该路径上各个边权值的总和。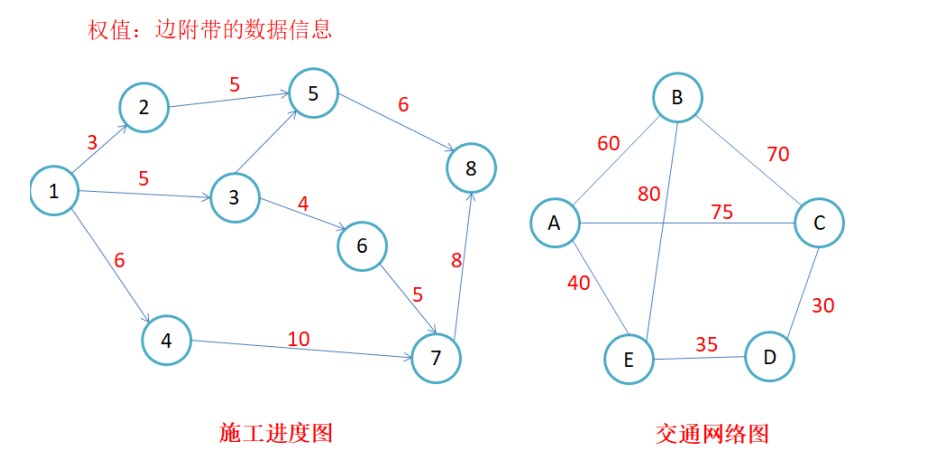

简单路径与回路：若路径上各顶点v1，v2，v3，…，vm均不重复，则称这样的路径为简单路径。若路 径上 第一个顶点v1和最后一个顶点vm重合，则称这样的路径为回路或环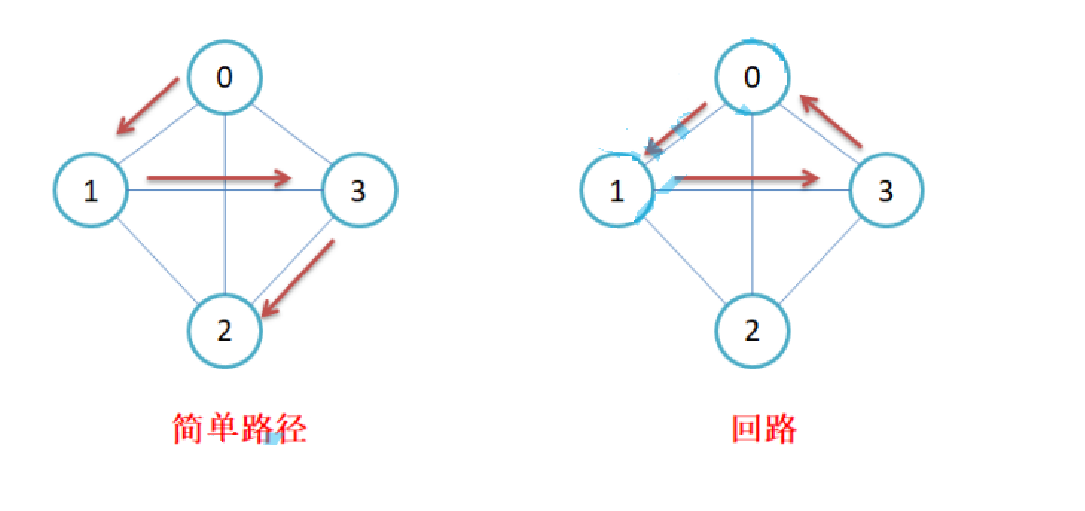

子图：设图G = {V, E}和图G1 = {V1 ，E1}，若V1属于V且E1属于E，则称G1是G的子图。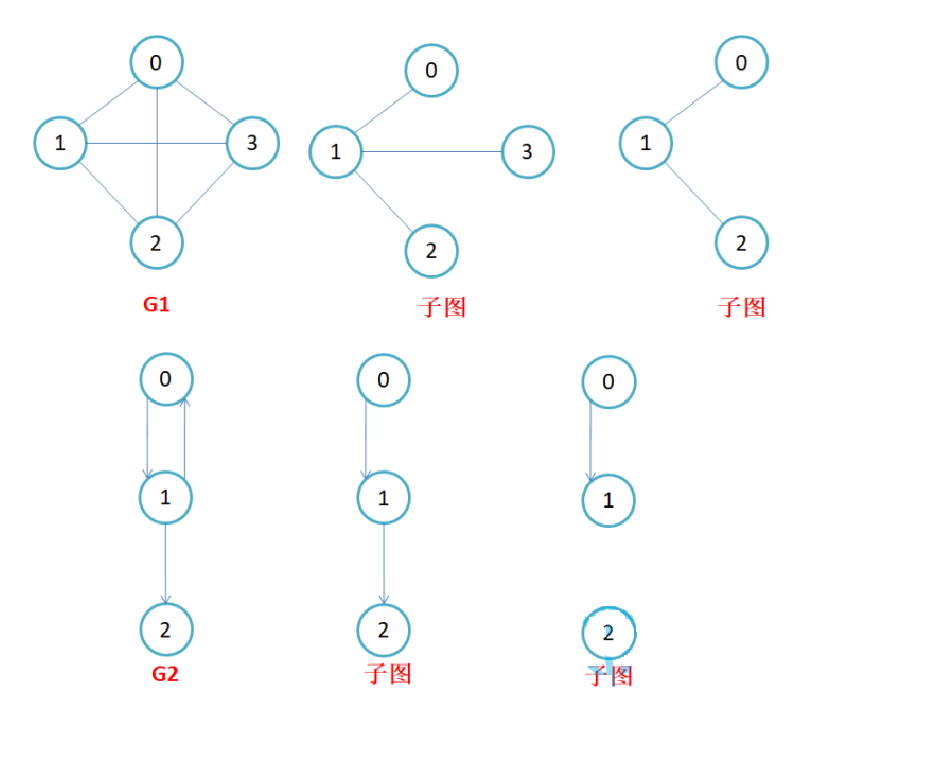

连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一 对顶点 都是连通的，则称此图为连通图。
强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到 vi的路 径，则称此图是强连通图。
生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。

1、如何存储图

因为图中既有节点，又有边(节点与节点之间的关系)，因此，在图的存储中，只需要保存：节点和边关系即可。节点保存比较简单，只需要一段连续空间即可，那边关系该怎么保存呢？

1-1、邻接矩阵

因为节点与节点之间的关系就是连通与否，即为0或者1，因此邻接矩阵(二维数组)即是：先用一个数组将定点保存，然后采用矩阵来表示节点与节点之间的关系。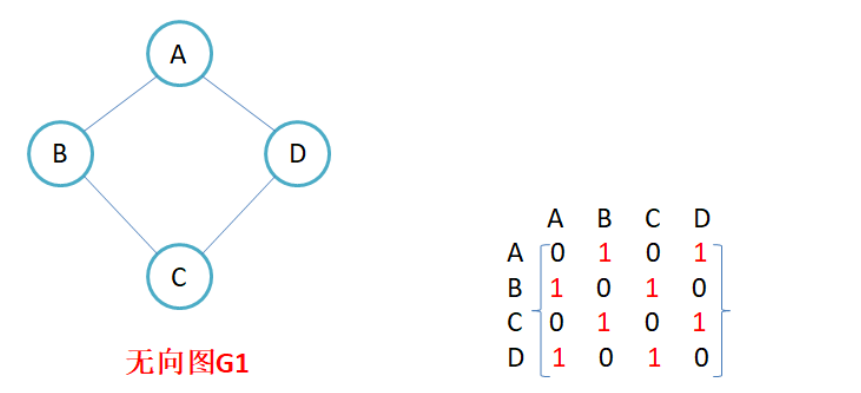


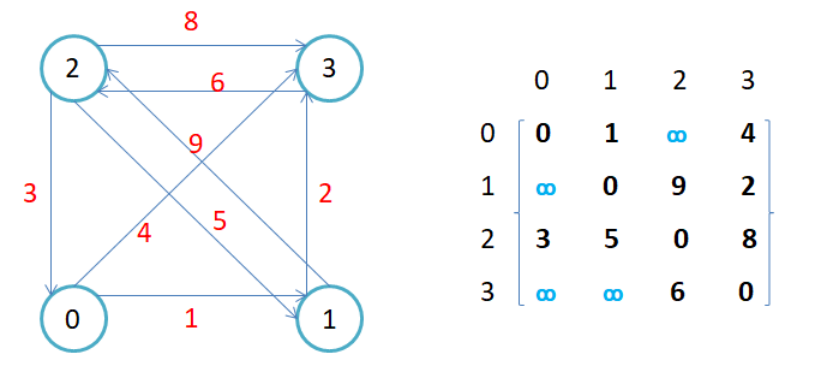
注意：

1. 无向图的邻接矩阵是对称的，第i行(列)元素之和，就是顶点i的度。有向图的邻接矩阵则不一定是对称的，第i行(列)元素之后就是顶点i 的出(入)度。
2. 如果边带有权值，并且两个节点之间是连通的，上图中的边的关系就用权值代替，如果两个顶点不通，则使用无穷大代替。
3. 邻接矩阵存储图的优点是能够快速知道两个顶点是否连通，缺陷是如果顶点比较多，边比较少时，矩阵中存储了大量的0成为系数矩阵，比较浪费空间，并且要求两个节点之间的路径不是很好求。

public class Constant {
    public static final int MAX = Integer.MAX_VALUE;
}

package org.example.graph;

import org.example.unionfindset.UnionFindSet;

import java.util.*;

/**
 * @Author 12629
 * @Description： 使用邻接矩阵来存储图
 */
public class GraphByMatrix {

    private char[] arrayV;//顶点数组
    private int[][] matrix;//矩阵
    private boolean isDirect;//是否是有向图

    /**
     * 此时
     * @param size 代表当前顶点的个数
     * @param isDirect
     */
    public GraphByMatrix(int size,boolean isDirect) {
        this.arrayV = new char[size];
        matrix = new int[size][size];
        for (int i = 0; i < size; i++) {
            Arrays.fill(matrix[i],Constant.MAX);
        }
        this.isDirect = isDirect;
    }

    public void initArrayV(char[] array) {
        for (int i = 0; i < array.length; i++) {
            arrayV[i] = array[i];
        }
    }

    /**
     *
     * @param srcV 起点
     * @param destV 终点
     * @param weight 权值
     */
    public void addEdge(char srcV,char destV,int weight) {
        int srcIndex = getIndexOfV(srcV);
        int destIndex = getIndexOfV(destV);
        matrix[srcIndex][destIndex] = weight;
        //如果是无向图 那么相反的位置 也同样需要置为空
        if(!isDirect) {
            matrix[destIndex][srcIndex] = weight;
        }
    }

    /**
     * 获取顶点V的下标
     * @param v
     * @return
     */
    private int getIndexOfV(char v) {
        for (int i = 0; i < arrayV.length; i++) {
            if(arrayV[i] == v) {
                return i;
            }
        }
        return -1;
    }

    /**
     * 获取顶点的度：有向图 = 入度+出度
     * @param v
     * @return
     */
    public int getDevOfV(char v) {
        int count = 0;

        int srcIndex = getIndexOfV(v);

        for (int i = 0; i < arrayV.length; i++) {
            if(matrix[srcIndex][i] != Constant.MAX) {
                count++;
            }
        }

        //计算有向图的入度
        if(isDirect) {
            for (int i = 0; i <  arrayV.length; i++) {
                if(matrix[i][srcIndex] != Constant.MAX) {
                    count++;
                }
            }
        }
        return count;
    }

    public void printGraph() {
        for (int i = 0; i < arrayV.length; i++) {
            System.out.print(arrayV[i]+" ");
        }
        System.out.println();
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[i].length; j++) {
                if(matrix[i][j] == Constant.MAX) {
                    System.out.print("∞ ");
                }else {
                    System.out.print(matrix[i][j]+" ");
                }
            }
            System.out.println();
        }
    }


    public void bfs(char v) {
        //1、定义一个visited数组 标记当前这个顶点是不是已经被 访问的
        boolean[] visited = new boolean[arrayV.length];
        //2、定义一个队列，来辅助完成广度优先遍历
        Queue<Integer> queue = new LinkedList<>();
        int srcIndex = getIndexOfV(v);
        queue.offer(srcIndex);
        while (!queue.isEmpty()) {
            int top = queue.poll();
            System.out.print(arrayV[top]+"->");
            visited[top] = true;//每次弹出一个元素 就置为true
            for (int i = 0; i < arrayV.length; i++) {
                if(matrix[top][i] != Constant.MAX && !visited[i]) {
                    queue.offer(i);
                    visited[i] = true;
                }
            }
        }
    }

    /**
     * 深度优先遍历
     * @param v
     */
    public void dfs(char v) {
        boolean[] visited = new boolean[arrayV.length];
        int srcIndex = getIndexOfV(v);
        dfsChild(srcIndex,visited);

    }

    private void dfsChild(int srcIndex,boolean[] visited) {
        System.out.print(arrayV[srcIndex]+"->");
        visited[srcIndex] = true;

        for (int i = 0; i < arrayV.length; i++) {
            if(matrix[srcIndex][i] != Constant.MAX && !visited[i]) {
                dfsChild(i,visited);
            }
        }
    }


    /**
     * 定义了一个边的抽象类
     */
    static class Edge {
        public int srcIndex;
        public int destIndex;
        public int weight;//权重

        public Edge(int srcIndex, int destIndex, int weight) {
            this.srcIndex = srcIndex;
            this.destIndex = destIndex;
            this.weight = weight;
        }
    }
    /**
     * 克鲁斯卡尔算法 实现
     * @param minTree
     * @return
     */
    public int kruskal(GraphByMatrix minTree) {
        //1、定义一个优先级队列 用来存储边
        PriorityQueue<Edge> minQ = new PriorityQueue<>(new Comparator<Edge>() {
            @Override
            public int compare(Edge o1, Edge o2) {
                return o1.weight - o2.weight;
            }
        });

        int n = arrayV.length;//顶点的个数
        //2. 遍历邻接矩阵，把所有的边，放到优先级队列当中
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if(i < j && matrix[i][j] != Constant.MAX) {
                    minQ.offer(new Edge(i,j,matrix[i][j]));
                }
            }
        }
        UnionFindSet ufs = new UnionFindSet(n);
        //3、开始从 优先级队列当中 取边
        int size = 0;
        int totalWight = 0;
        while (size < n-1 && !minQ.isEmpty()) {
            Edge edge = minQ.poll();
            int srcIndex = edge.srcIndex;
            int destIndex = edge.destIndex;

            if(!ufs.isSameUnionFindSet(srcIndex,destIndex)) {
                //添加到最小生成树当中
                minTree.addEdgeUseIndex(srcIndex,destIndex,matrix[srcIndex][destIndex]);
                System.out.println("选择的边："+arrayV[srcIndex]+"->"+
                        arrayV[destIndex]+":"+matrix[srcIndex][destIndex]);
                size++;//记录添加的边的条数
                totalWight+= matrix[srcIndex][destIndex];//记录最小生成树的 权值
                ufs.union(srcIndex,destIndex);
            }
        }

        if(size == n-1) {
            return totalWight;
        }else {
            return -1;//没有最小生成树
        }
    }

    private void addEdgeUseIndex(int srcIndex,int destIndex,int weight) {
        matrix[srcIndex][destIndex] = weight;
        //如果是无向图 那么相反的位置 也同样需要置为空
        if(!isDirect) {
            matrix[destIndex][srcIndex] = weight;
        }
    }

    public static void testGraphMinTree() {
        String str = "abcdefghi";
        char[] array =str.toCharArray();
        GraphByMatrix g = new GraphByMatrix(str.length(),false);
        g.initArrayV(array);

        g.addEdge('a', 'b', 4);
        g.addEdge('a', 'h', 8);
        //g.addEdge('a', 'h', 9);
        g.addEdge('b', 'c', 8);
        g.addEdge('b', 'h', 11);
        g.addEdge('c', 'i', 2);
        g.addEdge('c', 'f', 4);
        g.addEdge('c', 'd', 7);
        g.addEdge('d', 'f', 14);
        g.addEdge('d', 'e', 9);
        g.addEdge('e', 'f', 10);
        g.addEdge('f', 'g', 2);
        g.addEdge('g', 'h', 1);
        g.addEdge('g', 'i', 6);
        g.addEdge('h', 'i', 7);

        GraphByMatrix  kminTree = new GraphByMatrix(str.length(),false);
        System.out.println(g.kruskal(kminTree));
        kminTree.printGraph();
    }


    //起点
    public int prim(GraphByMatrix minTree,char chV) {
        int srcIndex = getIndexOfV(chV);
        //存储已经确定的点
        Set<Integer> setX = new HashSet<>();
        //先把确定的顶点放到集合当中
        setX.add(srcIndex);

        //初始化Y集合 ，存储的是 未确定的顶点
        Set<Integer> setY = new HashSet<>();
        int n = arrayV.length;
        for (int i = 0; i < n; i++) {
            if(i != srcIndex) {
                setY.add(i);
            }
        }

        //定义一个优先级队列
        PriorityQueue<Edge> minQ = new PriorityQueue<>(new Comparator<Edge>() {
            @Override
            public int compare(Edge o1, Edge o2) {
                return o1.weight - o2.weight;
            }
        });

        //遍历srcIndex连接出去的所边
        for (int i = 0; i < n; i++) {
            if(matrix[srcIndex][i] != Constant.MAX) {
                minQ.offer(new Edge(srcIndex,i,matrix[srcIndex][i]));
            }
        }

        int size = 0;
        int totalWeight = 0;
        //遍历优先级队列，取出n-1条边
        while (!minQ.isEmpty()) {
            Edge min = minQ.poll();
            int srcI = min.srcIndex;
            int desT = min.destIndex;

            if(setX.contains(desT)) {
                //构成环
                System.out.println("构成环的边："+arrayV[srcI]+"->"+
                        arrayV[desT]+":"+matrix[srcI][desT]);
            }else {
                minTree.addEdgeUseIndex(srcI,desT,min.weight);

                System.out.println("选择的边："+arrayV[srcI]+"->"+
                        arrayV[desT]+":"+matrix[srcI][desT]);

                totalWeight += min.weight;
                size++;
                if(size == n-1) {
                   return totalWeight;
                }
                //更新两个集合的
                setX.add(desT);
                setY.remove(desT);

                //把destI连接出去的所有边，也放到优先级队列当中
                for (int i = 0; i < n; i++) {
                    if(matrix[desT][i] != Constant.MAX && !setX.contains(i)) {
                        minQ.offer(new Edge(desT,i,matrix[desT][i]));
                    }
                }
            }
        }
        return -1;
    }

    public static void testGraphMinTreePrim() {
        String str = "abcdefghi";
        char[] array =str.toCharArray();
        GraphByMatrix g = new GraphByMatrix(str.length(),false);
        g.initArrayV(array);

        g.addEdge('a', 'b', 4);
        g.addEdge('a', 'h', 8);
        //g.addEdge('a', 'h', 9);
        g.addEdge('b', 'c', 8);
        g.addEdge('b', 'h', 11);
        g.addEdge('c', 'i', 2);
        g.addEdge('c', 'f', 4);
        g.addEdge('c', 'd', 7);
        g.addEdge('d', 'f', 14);
        g.addEdge('d', 'e', 9);
        g.addEdge('e', 'f', 10);
        g.addEdge('f', 'g', 2);
        g.addEdge('g', 'h', 1);
        g.addEdge('g', 'i', 6);
        g.addEdge('h', 'i', 7);

        GraphByMatrix  primTree = new GraphByMatrix(str.length(),false);
        System.out.println(g.prim(primTree,'a'));
        primTree.printGraph();

    }


    /**
     *
     * @param vSrc 指定的起点
     * @param dist 距离数组
     * @param pPath 路径
     */
    public void dijkstra(char vSrc,int[] dist,int[] pPath) {
        int srcIndex = getIndexOfV(vSrc);
        //距离数据初始化
        Arrays.fill(dist,Constant.MAX);
        dist[srcIndex] = 0;
        //路径数组初始化
        Arrays.fill(pPath,-1);
        pPath[srcIndex] = 0;
        //当前顶点是否被访问过？
        int n = arrayV.length;
        boolean[] s = new boolean[n];

        //n个顶点,要更新n次，每次都要从0下标开始，找到一个最小值
        for (int k = 0; k < n; k++) {
            int min = Constant.MAX;
            int u = srcIndex;
            for (int i = 0; i < n; i++) {
                if(s[i] == false && dist[i] < min) {
                    min = dist[i];
                    u = i;//更新u下标
                }
            }
            s[u] = true;//u:s
            //松弛u连接出去的所有的顶点 v
            for (int v = 0; v < n; v++) {
                if(s[v] == false && matrix[u][v] != Constant.MAX
                && dist[u] + matrix[u][v] < dist[v]) {
                    dist[v] = dist[u] + matrix[u][v];
                    pPath[v] = u;//更新当前的路径
                }
            }
        }
    }

    public void printShortPath(char vSrc,int[] dist,int[] pPath) {
        int srcIndex = getIndexOfV(vSrc);

        int n = arrayV.length;

        for (int i = 0; i < n; i++) {
            //i下标正好是起点  则不进行路径的打印
            if(i != srcIndex) {
                ArrayList<Integer> path = new ArrayList<>();
                int pathI = i;
                while (pathI != srcIndex) {
                    path.add(pathI);
                    pathI = pPath[pathI];
                }
                path.add(srcIndex);

                Collections.reverse(path);

                for (int pos : path) {
                    System.out.print(arrayV[pos]+" -> ");
                }
                System.out.println(dist[i]);
            }
        }
    }

    public static void testGraphDijkstra() {
        /*String str = "syztx";
        char[] array = str.toCharArray();
        GraphByMatrix g = new GraphByMatrix(str.length(),true);
        g.initArrayV(array);
        g.addEdge('s', 't', 10);
        g.addEdge('s', 'y', 5);
        g.addEdge('y', 't', 3);
        g.addEdge('y', 'x', 9);
        g.addEdge('y', 'z', 2);
        g.addEdge('z', 's', 7);
        g.addEdge('z', 'x', 6);
        g.addEdge('t', 'y', 2);
        g.addEdge('t', 'x', 1);
        g.addEdge('x', 'z', 4);*/

        /*
        搞不定负权值*/
        String str = "sytx";
        char[] array = str.toCharArray();
        GraphByMatrix g = new GraphByMatrix(str.length(),true);
        g.initArrayV(array);
        g.addEdge('s', 't', 10);
        g.addEdge('s', 'y', 5);
        g.addEdge('t', 'y', -7);
        g.addEdge('y', 'x', 3);

        int[] dist = new int[array.length];
        int[] parentPath = new int[array.length];
        g.dijkstra('s', dist, parentPath);

        System.out.println("dasfa");
        g.printShortPath('s', dist, parentPath);
    }


    public boolean bellmanFord(char vSrc,int[] dist,int[] pPath) {
        int srcIndex = getIndexOfV(vSrc);
        //距离数据初始化
        Arrays.fill(dist,Constant.MAX);
        dist[srcIndex] = 0;
        //路径数组初始化
        Arrays.fill(pPath,-1);
        pPath[srcIndex] = 0;

        int n = arrayV.length;

        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if(matrix[i][j] != Constant.MAX &&
                    dist[i] + matrix[i][j] < dist[j]) {
                        dist[j] = dist[i] + matrix[i][j];
                        pPath[j] = i;
                    }
                }
            }
        }

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if(matrix[i][j] != Constant.MAX &&
                        dist[i] + matrix[i][j] < dist[j]) {
                   return false;
                }
            }
        }
        return true;
    }

    public static void testGraphBellmanFord() {
        String str = "syztx";
        char[] array = str.toCharArray();
        GraphByMatrix g = new GraphByMatrix(str.length(),true);
        g.initArrayV(array);
        g.addEdge('s', 't', 6);
        g.addEdge('s', 'y', 7);
        g.addEdge('y', 'z', 9);
        g.addEdge('y', 'x', -3);
        g.addEdge('z', 's', 2);
        g.addEdge('z', 'x', 7);
        g.addEdge('t', 'x', 5);
        g.addEdge('t', 'y', 8);
        g.addEdge('t', 'z', -4);
        g.addEdge('x', 't', -2);

        //负权回路实例
       /* g.addEdge('s', 't', 6);
        g.addEdge('s', 'y', 7);
        g.addEdge('y', 'z', 9);
        g.addEdge('y', 'x', -3);
        g.addEdge('y', 's', 1);
        g.addEdge('z', 's', 2);
        g.addEdge('z', 'x', 7);
        g.addEdge('t', 'x', 5);
        g.addEdge('t', 'y', -8);
        g.addEdge('t', 'z', -4);
        g.addEdge('x', 't', -2);*/

        int[] dist = new int[array.length];
        int[] parentPath = new int[array.length];
        boolean flg = g.bellmanFord('s', dist, parentPath);
        if(flg) {
            g.printShortPath('s', dist, parentPath);
        }else {
            System.out.println("存在负权回路");
        }
    }


    public void floydWarShall(int[][] dist,int[][] pPath) {
        int n = arrayV.length;

        for (int i = 0; i < n; i++) {
            Arrays.fill(dist[i],Constant.MAX);
            Arrays.fill(pPath[i],-1);
        }

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if(matrix[i][j] != Constant.MAX) {
                    dist[i][j] = matrix[i][j];
                    pPath[i][j] = i;
                }else {
                    pPath[i][j] = -1;
                }
                if(i == j) {
                    dist[i][j] = 0;
                    pPath[i][j] = -1;
                }
            }
        }

        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if(dist[i][k] != Constant.MAX &&
                            dist[k][j] != Constant.MAX &&
                            dist[i][k] + dist[k][j] < dist[i][j]) {
                        dist[i][j] = dist[i][k] + dist[k][j];
                        //更新父节点下标
                        //pPath[i][j] = k;//不对
                        //如果经过了 i->k  k->j  此时是k
                        //i->x->s->k   k->..t->...x->j
                        pPath[i][j] = pPath[k][j];
                    }
                }
            }
            // 测试 打印权值和路径矩阵观察数据
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if(dist[i][j] == Constant.MAX) {
                        System.out.print(" * ");
                    }else{
                        System.out.print(dist[i][j]+" ");
                    }
                }
                System.out.println();
            }
            System.out.println("=========打印路径==========");
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    System.out.print(pPath[i][j]+" ");
                }
                System.out.println();
            }
            System.out.println("=================");
        }
    }

    public static void testGraphFloydWarShall() {
        String str = "12345";
        char[] array = str.toCharArray();
        GraphByMatrix g = new GraphByMatrix(str.length(),true);
        g.initArrayV(array);
        g.addEdge('1', '2', 3);
        g.addEdge('1', '3', 8);
        g.addEdge('1', '5', -4);
        g.addEdge('2', '4', 1);
        g.addEdge('2', '5', 7);
        g.addEdge('3', '2', 4);
        g.addEdge('4', '1', 2);
        g.addEdge('4', '3', -5);
        g.addEdge('5', '4', 6);

        int[][] dist = new int[array.length][array.length];
        int[][] parentPath = new int[array.length][array.length];
        g.floydWarShall(dist,parentPath);

        for (int i = 0; i < array.length; i++) {
            g.printShortPath(array[i],dist[i],parentPath[i]);
            System.out.println("************************");
        }
    }

    public static void main(String[] args) {
        testGraphFloydWarShall();
    }

    public static void main1(String[] args) {

        GraphByMatrix graph = new GraphByMatrix(4,false);
        char[] array = {'A','B','C','D'};
        graph.initArrayV(array);

        graph.addEdge('A','B',1);
        graph.addEdge('A','D',1);
        graph.addEdge('B','A',1);
        graph.addEdge('B','C',1);
        graph.addEdge('C','B',1);
        graph.addEdge('C','D',1);
        graph.addEdge('D','A',1);
        graph.addEdge('D','C',1);

        //graph.bfs('B');
        graph.dfs('B');
        //graph.printGraph();
        //System.out.println(graph.getDevOfV('A'));
    }

}

1-2、邻接表

邻接表：使用数组表示顶点的集合，使用链表表示边的关系。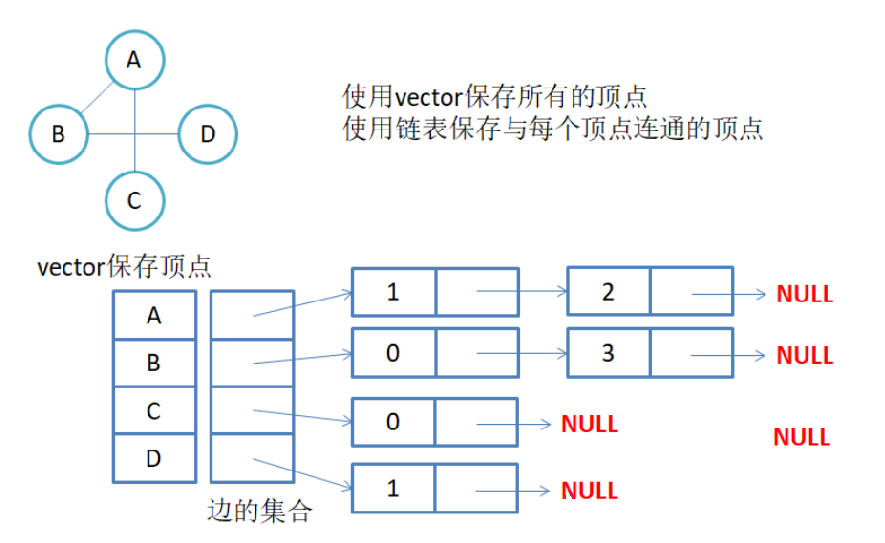

注意：无向图中同一条边在邻接表中出现了两次。如果想知道顶点vi的度，只需要知道顶点vi边链表集 合中结点的数目即可。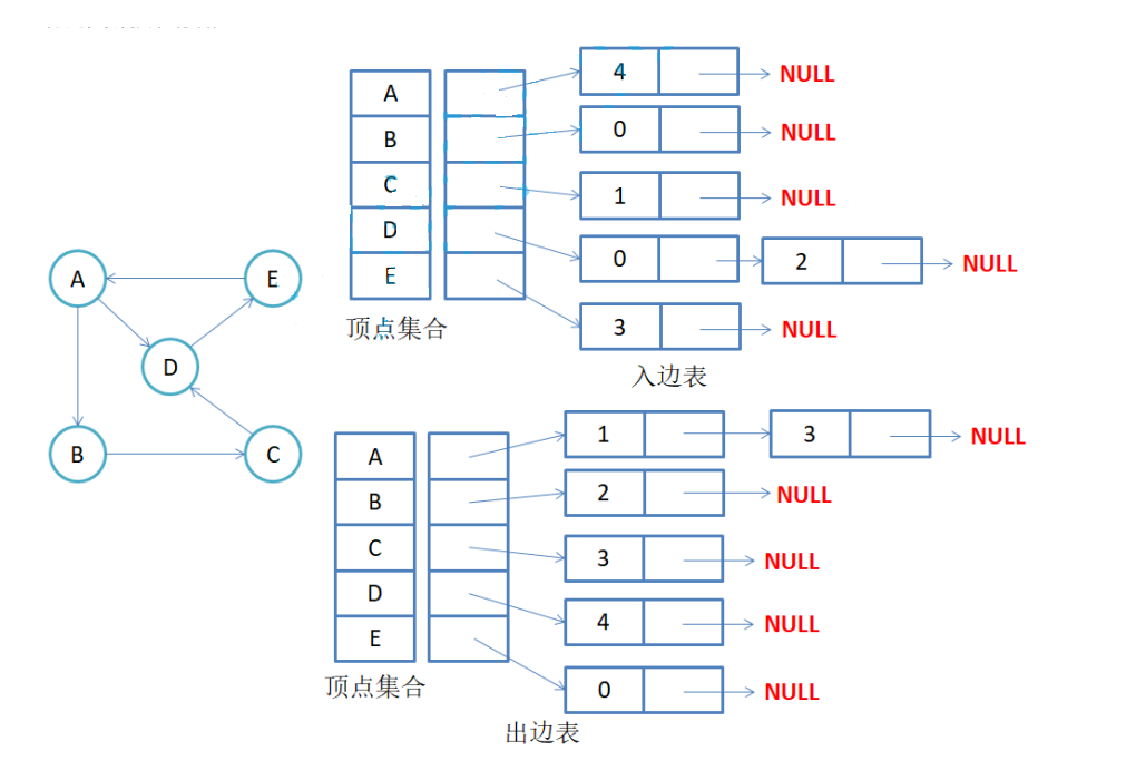

注意：有向图中每条边在邻接表中只出现一次，与顶点vi对应的邻接表所含结点的个数，就是该顶点的 出度，也称出度表，要得到vi顶点的入度，必须检测其他所有顶点对应的边链表，看有多少边顶点的dst 取值是i。

public class Constant {
    public static final int MAX = Integer.MAX_VALUE;
}

package org.example.graph;

import java.util.ArrayList;

public class GraphByNode {
    static class Node {
        public int src;//起始位置
        public int dest;//目标位置
        public int weight;//权重
        public Node next;

        public Node(int src, int dest, int weight) {
            this.src = src;
            this.dest = dest;
            this.weight = weight;
        }
    }

    public char[] arrayV;
    public ArrayList<Node> edgList;//存储边
    public boolean isDirect;

    public GraphByNode(int size,boolean isDirect) {
        this.arrayV = new char[size];
        edgList = new ArrayList<>(size);
        for (int i = 0; i < size; i++) {
            edgList.add(null);
        }
        this.isDirect = isDirect;
    }

    /**
     * 初始化顶点数组
     * @param array
     */
    public void initArrayV(char[] array) {
        for (int i = 0; i < array.length; i++) {
            arrayV[i] = array[i];
        }
    }

    /**
     * 添加边
     * @param srcV
     * @param destV
     * @param weight
     */
    public void addEdge(char srcV,char destV,int weight) {
        int srcIndex = getIndexOfV(srcV);
        int destIndex = getIndexOfV(destV);
        addEdgeChild(srcIndex,destIndex,weight);
        //无向图 需要添加两条边
        if(!isDirect) {
            addEdgeChild(destIndex,srcIndex,weight);
        }
    }

    private void addEdgeChild (int srcIndex , int destIndex,int weight) {
        //这里拿到是头节点
        Node cur = edgList.get(srcIndex);
        while (cur != null) {
            if(cur.dest == destIndex) {
                return;
            }
            cur = cur.next;
        }
        //之前没有存储过这条边
        Node node = new Node(srcIndex,destIndex,weight);
        node.next = edgList.get(srcIndex);
        edgList.set(srcIndex,node);
    }

    private int getIndexOfV(char v) {
        for (int i = 0; i < arrayV.length; i++) {
            if(arrayV[i] == v) {
                return i;
            }
        }
        return -1;
    }


    public void printGraph() {
        for (int i = 0; i < arrayV.length; i++) {
            System.out.print(arrayV[i]+"->");
            Node cur = edgList.get(i);
            while (cur != null) {
                System.out.print(arrayV[cur.dest]+" ->");
                cur = cur.next;
            }
            System.out.println();
        }
    }

    /**
     * 获取顶点的度
     * @param v
     * @return
     */
    public int getDevOfV(char v) {
        int count = 0;
        int srcIndex = getIndexOfV(v);
        Node cur = edgList.get(srcIndex);

        while (cur != null) {
            count++;
            cur = cur.next;
        }


        //只是计算了出度
        if(isDirect) {
            int destIndex = srcIndex;
            for (int i = 0; i < arrayV.length; i++) {
                if(i == destIndex) {
                    continue;
                }else {
                    Node pCur = edgList.get(i);
                    while (pCur != null) {
                        if(pCur.dest == destIndex) {
                            count++;
                        }
                        pCur = pCur.next;
                    }
                }
            }
        }
        return count;
    }

    public static void main(String[] args) {

        GraphByNode graph = new GraphByNode(4,true);
        char[] array = {'A','B','C','D'};
        graph.initArrayV(array);

        graph.addEdge('A','B',1);
        graph.addEdge('A','D',1);
        graph.addEdge('B','A',1);
        graph.addEdge('B','C',1);
        graph.addEdge('C','B',1);
        graph.addEdge('C','D',1);
        graph.addEdge('D','A',1);
        graph.addEdge('D','C',1);

        System.out.println("getDevOfV:: "+graph.getDevOfV('A'));
        graph.printGraph();
    }

}

2、图的遍历

给定一个图G和其中任意一个顶点v0，从v0出发，沿着图中各边访问图中的所有顶点，且每个顶点仅被遍历 一次。"遍历"即对结点进行某种操作的意思。 请思考树以前是怎么遍历的，此处可以直接用来遍历图吗？为什么？

2-1、图的广度优先遍历（层序遍历）

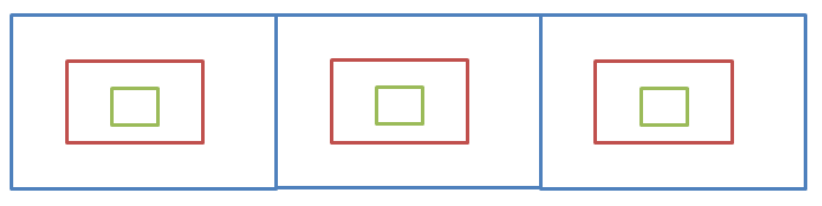
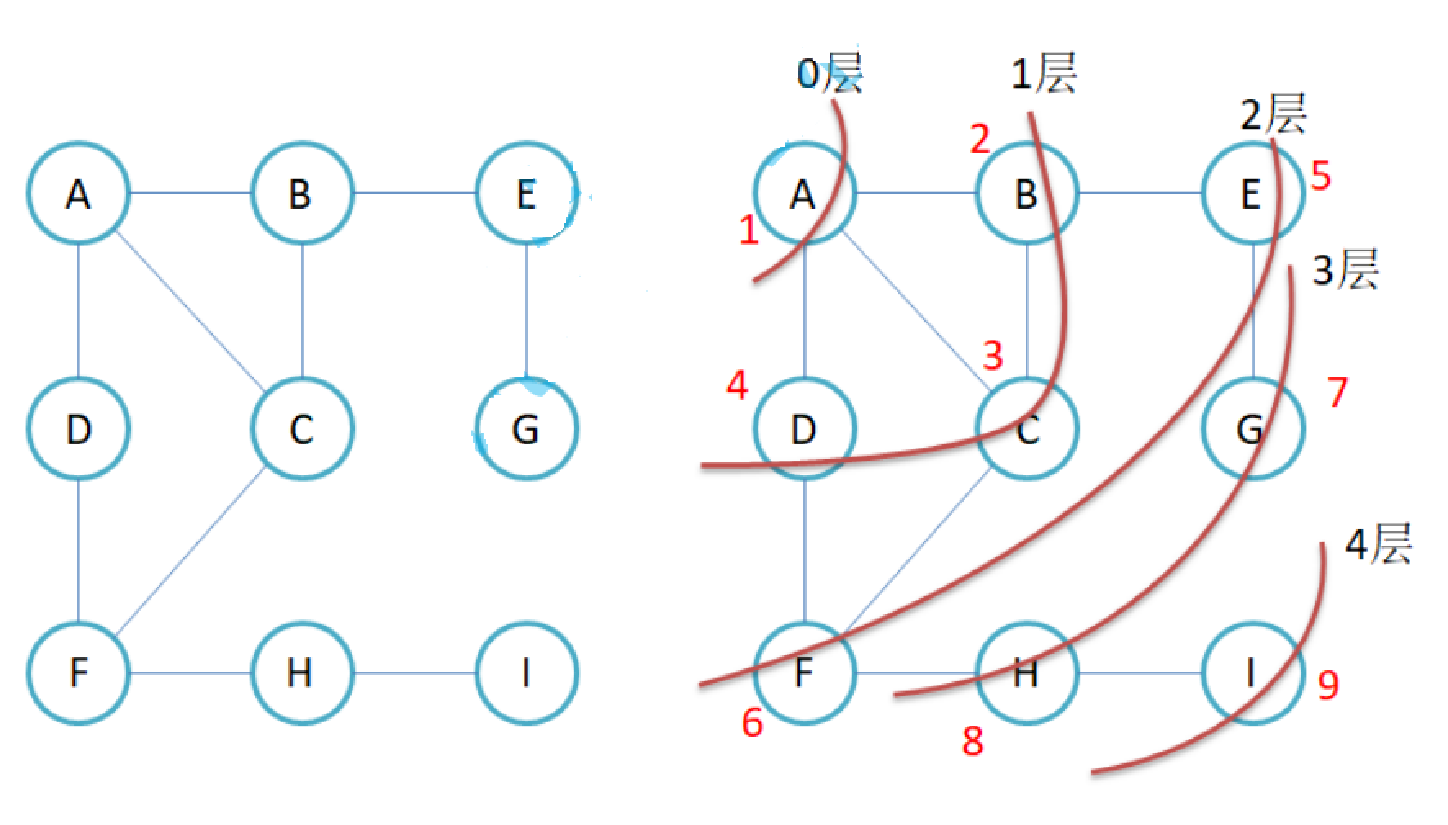
比如现在要找东西，假设有三个抽屉，东西在那个抽屉不清楚，现在要将其找到，广度优先遍历的做法是:

1. 先将三个抽屉打开，在最外层找一遍。
2. 将每个抽屉中红色的盒子打开，再找一遍。
3. 将红色盒子中绿色盒子打开，再找一遍。

直到找完所有的盒子，注意:每个盒子只能找一次，不能重复找。

public void bfs(char v) {
//1、定义一个visited数组 标记当前这个顶点是不是已经被 访问的
boolean[] visited = new boolean[arrayV.length];
//2、定义一个队列，来辅助完成广度优先遍历
Queue<Integer> queue = new LinkedList<>();
int srcIndex = getIndexOfV(v);
queue.offer(srcIndex);
while (!queue.isEmpty()) {
    int top = queue.poll();
    System.out.print(arrayV[top]+"->");
    visited[top] = true;//每次弹出一个元素 就置为true
    for (int i = 0; i < arrayV.length; i++) {
        if(matrix[top][i] != Constant.MAX && !visited[i]) {
            queue.offer(i);
            visited[i] = true;
        }
    }
}
}

2-2、图的深度优先遍历

比如现在要找东西，假设有三个抽屉，东西在那个抽不清楚，现在要将其找到，广度优先遍历的做法是:

1. 先将第一个抽屉打开，在最外层找一遍
2. 将第一个抽屉中红盒子打开，在红盒子中找一遍
3. 将红盒子中绿盒子打开，在绿盒子中找一遍
4. 递归查找剩余的两个盒子

深度优先遍历:将一个抽屉一次性遍历完(包括该抽屉中包含的小盒子)，再去递归遍历其他盒子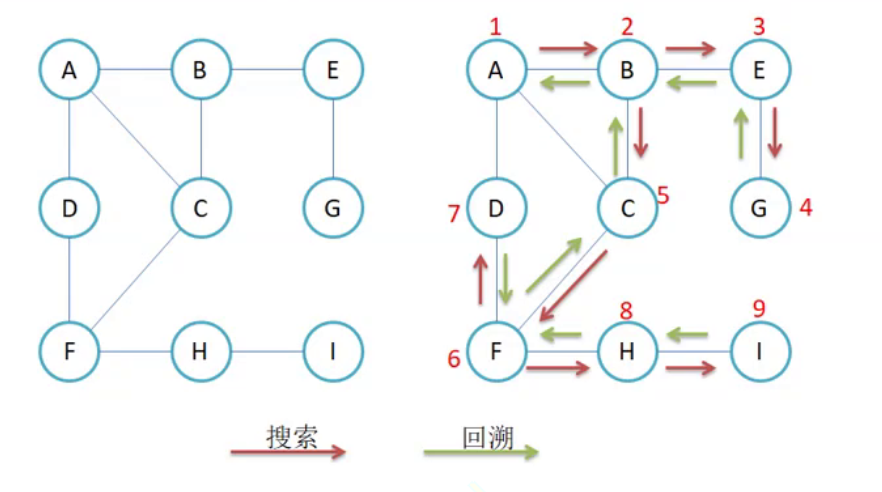

public void dfs(char v) {
boolean[] visited = new boolean[arrayV.length];
int srcIndex = getIndexOfV(v);
dfsChild(srcIndex,visited);

}

private void dfsChild(int srcIndex,boolean[] visited) {
    System.out.print(arrayV[srcIndex]+"->");
    visited[srcIndex] = true;

    for (int i = 0; i < arrayV.length; i++) {
        if(matrix[srcIndex][i] != Constant.MAX && !visited[i]) {
            dfsChild(i,visited);
        }
    }
}

3、图的最小生成树

连通图中的每一棵生成树，都是原图的一个极大无环子图，即：**从其中删去任何一条边，生成树就不在连通；反之，在其中引入任何一条新边，都会形成一条回路。 **
**若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。**因此构造最小生成树的准则有三条：

1. 只能使用图中的边来构造最小生成树。
2. 只能使用恰好n-1条边来连接图中的n个顶点。
3. 选用的n-1条边不能构成回路。

构造最小生成树的方法：Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。
贪心算法：是指在问题求解时，总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体最优的 的选择，而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解。

3-1、Kruskal算法

Kruskal算法是一种用于查找图的最小生成树（Minimum Spanning Tree, MST）的贪心算法。最小生成树是连接图中所有顶点的边的集合，并且这些边的总权重最小，同时还要保证这些顶点是连通的。Kruskal算法的基本思想是按照边的权重从小到大的顺序选择边，但是要保证加上这条边后不会导致图中出现环。Kruskal算法的步骤如下：

1. 排序：将图中的所有边按照权重从小到大排序。
2. 初始化：创建一个空的边集合，用于存放最终的最小生成树的边。
3. 遍历：按照排序后的顺序，依次考虑每条边。
   • 如果加入这条边后不会导致图中出现环，则将这条边加入到最小生成树的边集合中。
4. 检查环：可以使用并查集（Union-Find）数据结构来快速判断加入一条边是否会导致环的产生。
5. 结束条件：当边集合中的边数等于图中顶点数减一时，或者所有边都被考虑过时，算法结束。

Kruskal算法的时间复杂度主要取决于边的排序和并查集的操作。如果使用优先队列（例如最小堆）来排序边，时间复杂度为O(E log E)，其中E是边的数量。并查集的操作（查找和合并）的时间复杂度为O(α(N))，其中N是顶点数，α是阿克曼函数的反函数，通常认为α(N)的增长速度非常慢，对于实际问题可以近似认为是常数。
Kruskal算法适用于边稠密的图，因为它首先考虑的是边的权重，而不是顶点的连接情况。与之相对的是Prim算法，它是一种基于顶点的贪心算法，适用于顶点稠密的图。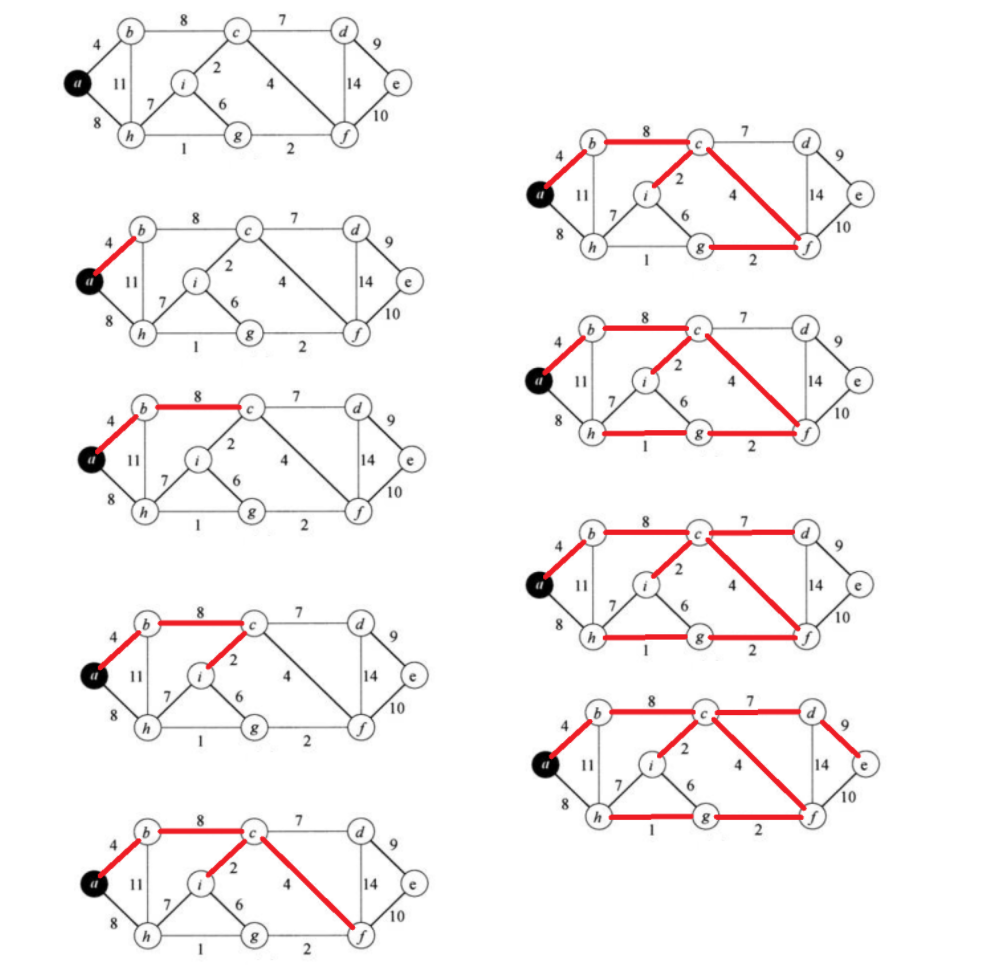

总结：每次寻找全局最小的不构成环的边。
两个问题：
1、如何找到最小的边：优先级队列（小根堆）。
2、如何判断是否成环：使用并查集判断两个节点是否在同一个集合里面，这条边的两个点在同一个集合里面，就说明加上这条边就会成环。

public int kruskal(GraphByMatrix minTree) {
//1、定义一个优先级队列 用来存储边
PriorityQueue<Edge> minQ = new PriorityQueue<>(new Comparator<Edge>() {
    @Override
    public int compare(Edge o1, Edge o2) {
        return o1.weight - o2.weight;
    }
});

int n = arrayV.length;//顶点的个数
//2. 遍历邻接矩阵，把所有的边，放到优先级队列当中
for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        if(i < j && matrix[i][j] != Constant.MAX) {
            minQ.offer(new Edge(i,j,matrix[i][j]));
        }
    }
}
UnionFindSet ufs = new UnionFindSet(n);
//3、开始从 优先级队列当中 取边
int size = 0;
int totalWight = 0;
while (size < n-1 && !minQ.isEmpty()) {
    Edge edge = minQ.poll();
    int srcIndex = edge.srcIndex;
    int destIndex = edge.destIndex;

    if(!ufs.isSameUnionFindSet(srcIndex,destIndex)) {
        //添加到最小生成树当中
        minTree.addEdgeUseIndex(srcIndex,destIndex,matrix[srcIndex][destIndex]);
        System.out.println("选择的边："+arrayV[srcIndex]+"->"+
                           arrayV[destIndex]+":"+matrix[srcIndex][destIndex]);
        size++;//记录添加的边的条数
        totalWight+= matrix[srcIndex][destIndex];//记录最小生成树的 权值
        ufs.union(srcIndex,destIndex);
    }
}

if(size == n-1) {
    return totalWight;
}else {
    return -1;//没有最小生成树
}
}

private void addEdgeUseIndex(int srcIndex,int destIndex,int weight) {
    matrix[srcIndex][destIndex] = weight;
    //如果是无向图 那么相反的位置 也同样需要置为空
    if(!isDirect) {
        matrix[destIndex][srcIndex] = weight;
    }
}

import java.util.Arrays;

public class UnionFindSet {
    public int[] elem;

    public UnionFindSet(int n) {
        this.elem = new int[n];
        Arrays.fill(elem,-1);
    }

    /**
     * 查找数据x 的根节点
     * @param x
     * @return 下标
     */
    public int findRoot(int x) {
        if(x < 0) {
            throw new IndexOutOfBoundsException("下标不合法，是负数");
        }
        while (elem[x] >= 0 ) {
            x = elem[x];//1  0
        }
        return x;
    }

    /**
     * 查询x1 和 x2 是不是同一个集合
     * @param x1
     * @param x2
     * @return
     */
    public boolean isSameUnionFindSet(int x1,int x2) {
        int index1 = findRoot(x1);
        int index2 = findRoot(x2);
        if(index1 == index2) {
            return true;
        }
        return false;
    }

    /**
     * 这是合并操作
     * @param x1
     * @param x2
     */
    public void union(int x1,int x2) {
        int index1 = findRoot(x1);
        int index2 = findRoot(x2);
        if(index1 == index2) {
            return;
        }
        elem[index1] = elem[index1] + elem[index2];
        elem[index2] = index1;
    }

    public int getCount() {
        int count = 0;
        for (int x : elem) {
            if(x <  0) {
                count++;
            }
        }
        return count;
    }

    public void print() {
        for (int x : elem) {
            System.out.print(x+" ");
        }
        System.out.println();
    }

    //省份的数量
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        UnionFindSet ufs = new UnionFindSet(n);
        for(int i = 0;i < isConnected.length;i++) {
            for(int j = 0;j < isConnected[i].length;j++) {
                if(isConnected[i][j] == 1) {
                    ufs.union(i,j);
                }
            }
        }
        return ufs.getCount();
    }

    //等式的满足性
    public boolean equationsPossible(String[] equations) {
        UnionFindSet ufs = new UnionFindSet(26);
        for(int i = 0; i < equations.length;i++) {
            if(equations[i].charAt(1) == '=') {
                ufs.union(equations[i].charAt(0)-'a',equations[i].charAt(3)-'a');
            }
        }
        for(int i = 0; i < equations.length;i++) {
            if(equations[i].charAt(1) == '!') {
                int index1 = ufs.findRoot(equations[i].charAt(0)-'a');
                int index2 = ufs.findRoot(equations[i].charAt(3)-'a');
                if(index1 == index2) {
                    return false;
                }
            }
        }
        return true;
    }

    public static void main(String[] args) {
        String[] str = {"a==b","b!=a"};
        //equationsPossible(str);
    }

    //亲戚题
    public static void main2(String[] args) {
        int n = 10;
        int m = 3;
        int p = 2;

        UnionFindSet unionFindSet = new UnionFindSet(n);

        System.out.println("合并：0和6：");
        unionFindSet.union(0,6);
        unionFindSet.union(0,1);
        System.out.println("合并：3和7：");
        unionFindSet.union(3,7);
        System.out.println("合并：4和8：");
        unionFindSet.union(4,8);

        System.out.println("以下是不是亲戚：");
        boolean flg = unionFindSet.isSameUnionFindSet(1,8);
        if(flg) {
            System.out.println("是亲戚！");
        }else {
            System.out.println("不是亲戚！");
        }
        System.out.println("当亲的亲戚关系 "+unionFindSet.getCount()+" 对！");
    }

    public static void main1(String[] args) {
        UnionFindSet unionFindSet = new UnionFindSet(10);
        System.out.println("合并：0和6：");
        unionFindSet.union(0,6);
        System.out.println("合并：0和7：");
        unionFindSet.union(0,7);
        System.out.println("合并：0和8：");
        unionFindSet.union(0,8);

        System.out.println("合并：1和4：");
        unionFindSet.union(1,4);
        System.out.println("合并：1和9：");
        unionFindSet.union(1,9);
        System.out.println("合并：2和3：");
        unionFindSet.union(2,3);

        System.out.println("合并：2和5：");
        unionFindSet.union(2,5);

        unionFindSet.print();

        System.out.println("合并：8和1：");
        unionFindSet.union(8,1);

        unionFindSet.print();

        System.out.println("查找是不是同一个集合");
        System.out.println(unionFindSet.isSameUnionFindSet(6, 9));
        System.out.println(unionFindSet.isSameUnionFindSet(8, 2));

    }
}

3-2、Prim算法

Prim算法是一种用于寻找图的最小生成树（MST）的算法。以下是Prim算法的详细步骤：

1. 选择起始顶点：从图中任意选择一个顶点作为起始点，并将其加入到最小生成树的集合中。
2. 初始化：创建一个优先队列（最小堆），用于存储所有从已选择顶点到未选择顶点的边，以及这些边的权重。
3. 循环：在图中还有未选择的顶点时，重复以下步骤：
   • 从优先队列中取出权重最小的边。这条边连接一个已选择的顶点和一个未选择的顶点。
   • 将这条边添加到最小生成树中，并将对应的未选择顶点加入到已选择顶点集合中。
   • 更新优先队列：将所有从新加入的顶点出发的边加入到优先队列中，如果这些边的另一端顶点还未被选择。
4. 结束条件：当所有顶点都被包含在最小生成树中，或者优先队列变空时，算法结束。

Prim算法的时间复杂度主要取决于优先队列的操作。如果使用普通的优先队列，算法的时间复杂度为O(E log V)，其中E是边的数量，V是顶点的数量。如果使用斐波那契堆作为优先队列，算法的时间复杂度可以降低到O(E + V log V)。
Prim算法适用于顶点稠密的图，因为它每次都是选择连接到已选择顶点集合的最小边，而不是像Kruskal算法那样选择全局最小的边。这使得Prim算法在顶点数量远大于边的数量时效率更高。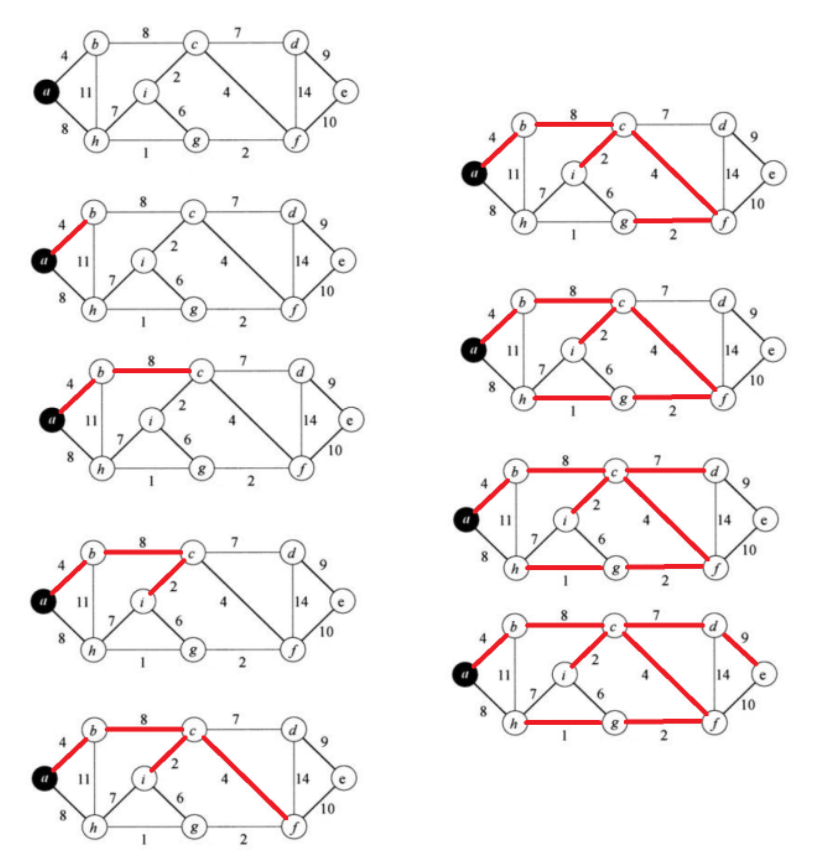

public int prim(GraphByMatrix minTree,char chV) {
        int srcIndex = getIndexOfV(chV);
        //存储已经确定的点
        Set<Integer> setX = new HashSet<>();
        //先把确定的顶点放到集合当中
        setX.add(srcIndex);

        //初始化Y集合 ，存储的是 未确定的顶点
        Set<Integer> setY = new HashSet<>();
        int n = arrayV.length;
        for (int i = 0; i < n; i++) {
            if(i != srcIndex) {
                setY.add(i);
            }
        }

        //定义一个优先级队列
        PriorityQueue<Edge> minQ = new PriorityQueue<>(new Comparator<Edge>() {
            @Override
            public int compare(Edge o1, Edge o2) {
                return o1.weight - o2.weight;
            }
        });

        //遍历srcIndex连接出去的所边
        for (int i = 0; i < n; i++) {
            if(matrix[srcIndex][i] != Constant.MAX) {
                minQ.offer(new Edge(srcIndex,i,matrix[srcIndex][i]));
            }
        }

        int size = 0;
        int totalWeight = 0;
        //遍历优先级队列，取出n-1条边
        while (!minQ.isEmpty()) {
            Edge min = minQ.poll();
            int srcI = min.srcIndex;
            int desT = min.destIndex;

            if(setX.contains(desT)) {
                //构成环
                System.out.println("构成环的边："+arrayV[srcI]+"->"+
                        arrayV[desT]+":"+matrix[srcI][desT]);
            }else {
                minTree.addEdgeUseIndex(srcI,desT,min.weight);

                System.out.println("选择的边："+arrayV[srcI]+"->"+
                        arrayV[desT]+":"+matrix[srcI][desT]);

                totalWeight += min.weight;
                size++;
                if(size == n-1) {
                   return totalWeight;
                }
                //更新两个集合的
                setX.add(desT);
                setY.remove(desT);

                //把destI连接出去的所有边，也放到优先级队列当中
                for (int i = 0; i < n; i++) {
                    if(matrix[desT][i] != Constant.MAX && !setX.contains(i)) {
                        minQ.offer(new Edge(desT,i,matrix[desT][i]));
                    }
                }
            }
        }
        return -1;
    }

从某一个点开始，局部选择权值最小的不成环的路径，局部选择是指与已选顶点相连的那些边。

两个问题：
如何选怎局部最小边：每加入一个顶点，就将与该顶点相连的边为选怎的边加入到优先级队列中
如何判断环路：并查集。

4、最短路径

最短路径问题：从在带权图的某一顶点出发，找出一条通往另一顶点的最短路径，最短也就是沿路径各边的权值总 和达到最小。

4-1、 单源最短路径–Dijkstra算法

单源最短路径问题：给定一个图G = ( V ， E ) G=(V，E)G=(V，E)，求源结点s ∈ V s∈Vs∈V到图中每个结点v ∈ V v∈Vv∈V的最短路径。Dijkstra算法就适用于解决带权重的有向图上的单源最短路径问题，同时算法要 求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点和一个终点，所以使用Dijkstra算法 求解过后也就得到了所需起点到终点的最短路径。 针对一个带权有向图G，将所有结点分为两组S和Q，S是已经确定最短路径的结点集合，在初始时为空（初始 时就可以将源节点s放入，毕竟源节点到自己的代价是0），Q 为其余未确定最短路径的结点集合，每次从Q 中找出一个起点到该结点代价最小的结点u ，将u 从Q 中移出，并放入S 中，对u 的每一个相邻结点v 进行松 弛操作。松弛即对每一个相邻结点v ，判断源节点s到结点u 的代价与u 到v 的代价之和是否比原来s 到v 的代 价更小，若代价比原来小则要将s 到v 的代价更新为s 到u 与u 到v 的代价之和，否则维持原样。如此一直循 环直至集合Q 为空，即所有节点都已经查找过一遍并确定了最短路径，至于一些起点到达不了的结点在算法 循环后其代价仍为初始设定的值，不发生变化。Dijkstra算法每次都是选择V-S中最小的路径节点来进行更 新，并加入S中，所以该算法使用的是贪心策略。** Dijkstra算法存在的问题是不支持图中带负权路径，如果带有负权路径，则可能会找不到一些路径的最短路径。 **

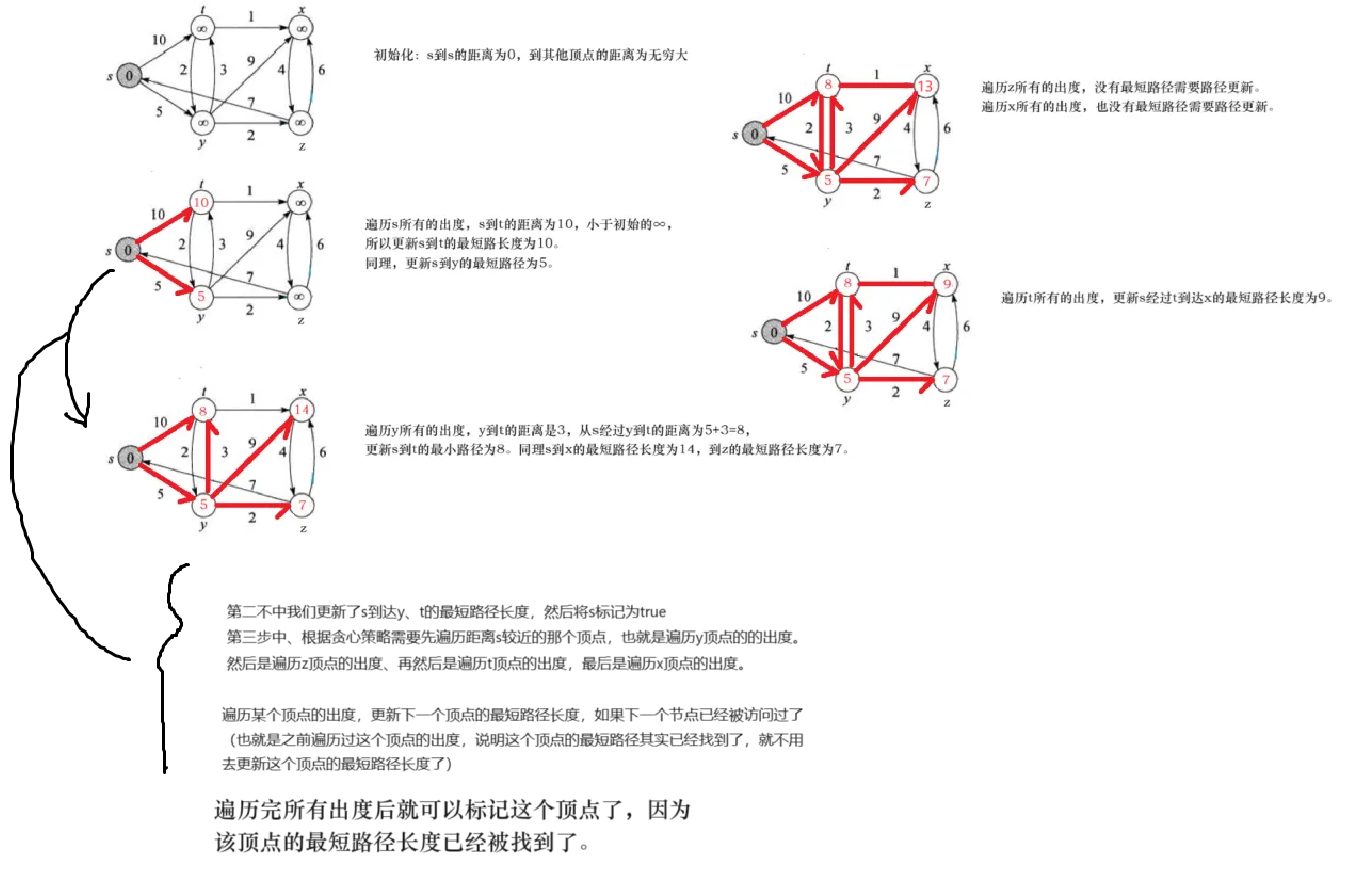
第一步初始化，第二步遍历s的出度跟新了到达y、t的最短距离，在第三步中可以选择遍历y的出度，也可以选择遍历t的出度，Dijkstra算法是选择先遍历小的哪一个也就是y顶点。
算法中添加了cheak数组第三步中y顶点已经被遍历过来标记cheak[y]=true;当遍历t的时候就不会在从t走向y了，因为权值都是正数，而刚才在选择先遍历谁的时候就已经说明从s到y比s到t近、说明s经过t在到达y的距离只会更远，所以当cheak[y]被标记后说明s到y的最短路径已经找到了，后续经过别的顶点也可到y顶点的路径不可能会更小了。

public void dijkstra(char vSrc,int[] dist,int[] pPath) {
    int srcIndex = getIndexOfV(vSrc);
    //距离数据初始化
    Arrays.fill(dist,Constant.MAX);
    dist[srcIndex] = 0;
    //路径数组初始化
    Arrays.fill(pPath,-1);
    pPath[srcIndex] = 0;
    //当前顶点是否被访问过？
    int n = arrayV.length;
    boolean[] s = new boolean[n];

    //n个顶点,要更新n次，每次都要从0下标开始，找到一个最小值
    for (int k = 0; k < n; k++) {
        int min = Constant.MAX;
        int u = srcIndex;
        for (int i = 0; i < n; i++) {
            if(s[i] == false && dist[i] < min) {
                min = dist[i];
                u = i;//更新u下标
            }
        }
        s[u] = true;//u:s
        //松弛u连接出去的所有的顶点 v
        for (int v = 0; v < n; v++) {
            if(s[v] == false && matrix[u][v] != Constant.MAX
               && dist[u] + matrix[u][v] < dist[v]) {
                dist[v] = dist[u] + matrix[u][v];
                pPath[v] = u;//更新当前的路径
            }
        }
    }
}

public void printShortPath(char vSrc,int[] dist,int[] pPath) {
    int srcIndex = getIndexOfV(vSrc);

    int n = arrayV.length;

    for (int i = 0; i < n; i++) {
        //i下标正好是起点  则不进行路径的打印
        if(i != srcIndex) {
            ArrayList<Integer> path = new ArrayList<>();
            int pathI = i;
            while (pathI != srcIndex) {
                path.add(pathI);
                pathI = pPath[pathI];
            }
            path.add(srcIndex);

            Collections.reverse(path);

            for (int pos : path) {
                System.out.print(arrayV[pos]+" -> ");
            }
            System.out.println(dist[i]);
        }
    }
}

4-2、 单源最短路径–Bellman-Ford算法

Dijkstra算法只能用来解决正权图的单源最短路径问题，但有些题目会出现负权图。这时这个算法就不能帮助 我们解决问题了，而bellman—ford算法可以解决负权图的单源最短路径问题。它的优点是可以解决有负权 边的单源最短路径问题，而且可以用来判断是否有负权回路。它也有明显的缺点，它的时间复杂度 O(N*E) (N是点数，E是边数)普遍是要高于Dijkstra算法O(N²)的。像这里如果我们使用邻接矩阵实现，那么遍历所有 边的数量的时间复杂度就是O(N^3)，这里也可以看出来Bellman-Ford就是一种暴力求解更新。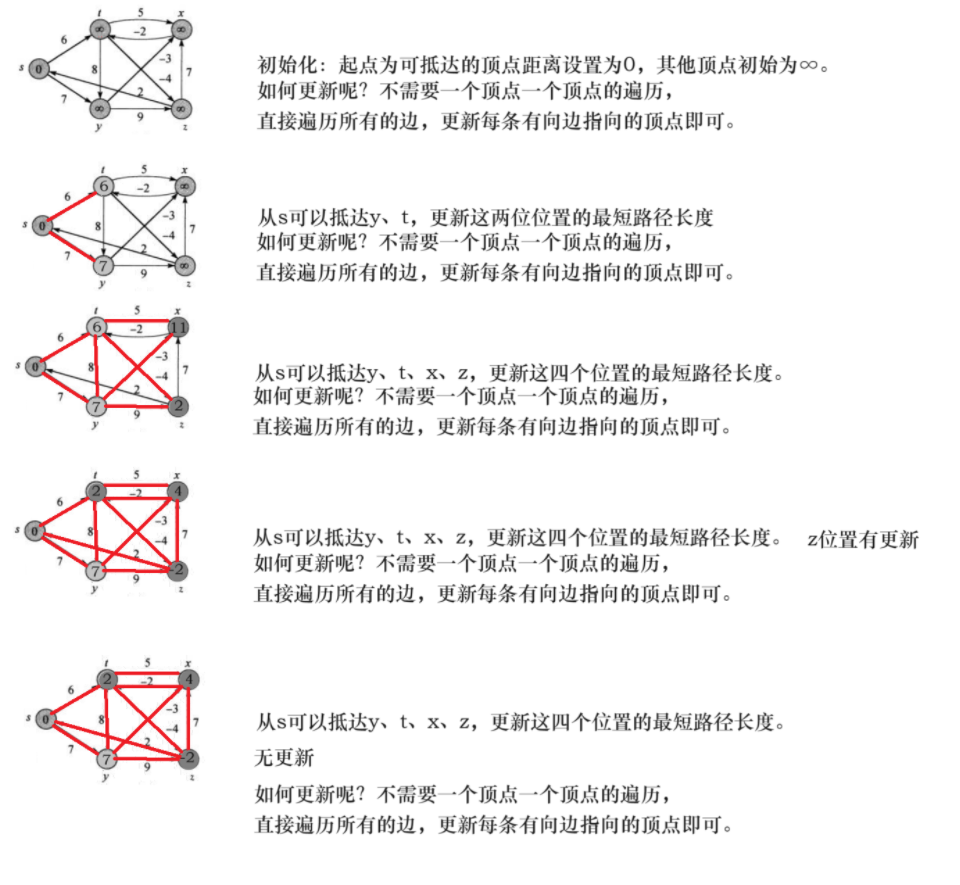

该算法计算谋起点到其他顶点的最短距离，如果有负权回路，一直转圈路径和一直减小，这种情况则返回false。如果没有负权回路，返回ture,可以找到每个顶点的最短路径。
如何判断是否有负权回路：在执行一次循环体即可，若有负权回路存在，每次指向循环体相当于围着负权回路绕了一圈，就会有顶点的最短路径更新，此时直接判定为有负权回路存在，返回false，如果循环体执行后没有顶点的最短路径更新，说明从起点到所有顶点的最短路径都已经找了，该图没有负权回路，返回true。

、public boolean bellmanFord(char vSrc,int[] dist,int[] pPath) {
    int srcIndex = getIndexOfV(vSrc);
    //距离数据初始化
    Arrays.fill(dist,Constant.MAX);
    dist[srcIndex] = 0;
    //路径数组初始化
    Arrays.fill(pPath,-1);
    pPath[srcIndex] = 0;

    int n = arrayV.length;

    for (int k = 0; k < n; k++) {
        // i，j循环是在遍历说有的边，可以改成双重循环
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if(matrix[i][j] != Constant.MAX &&
                   dist[i]!=Constant.MAX &&
                   dist[i] + matrix[i][j] < dist[j]) {
                    dist[j] = dist[i] + matrix[i][j];
                    pPath[j] = i;
                }
            }
        }
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if(matrix[i][j] != Constant.MAX &&
               dist[i] + matrix[i][j] < dist[j]) {
                return false;
            }
        }
    }
    return true;
}

public class BellmanFord {

    // 用于表示图中的边
    static class Edge {
        int source, dest, weight;

        Edge(int source, int dest, int weight) {
            this.source = source;
            this.dest = dest;
            this.weight = weight;
        }
    }

    // 执行Bellman-Ford算法
    static boolean bellmanFord(int V, Edge[] edges, int source) {
        // 从源点到所有顶点的距离初始化为无穷大，除了源点自身
        int[] distance = new int[V];
        for (int i = 0; i < V; i++) {
            distance[i] = Integer.MAX_VALUE;
        }
        distance[source] = 0;

        // 遍历所有边V-1次
        for (int i = 1; i < V; i++) {
            for (Edge edge : edges) {
                if (distance[edge.source] != Integer.MAX_VALUE &&
                    distance[edge.source] + edge.weight < distance[edge.dest]) {
                    distance[edge.dest] = distance[edge.source] + edge.weight;
                }
            }
        }

        // 检查是否存在负权重环
        for (Edge edge : edges) {
            if (distance[edge.source] != Integer.MAX_VALUE &&
                distance[edge.source] + edge.weight < distance[edge.dest]) {
                return false; // 如果可以进一步更新距离，说明存在负权重环
            }
        }

        return true; // 图中不存在负权重环
    }

    // 主函数，用于测试Bellman-Ford算法
    public static void main(String[] args) {
        int V = 5; // 顶点的数量
        Edge[] edges = new Edge[] {
            new Edge(0, 1, -1), new Edge(0, 2, 4),
            new Edge(1, 2, 3), new Edge(1, 3, 2),
            new Edge(1, 4, 2), new Edge(3, 1, 1),
            new Edge(4, 0, 6), new Edge(4, 3, -3)
        };

        boolean hasNegativeCycle = bellmanFord(V, edges, 0);
        if (hasNegativeCycle) {
            System.out.println("Graph contains a negative weight cycle");
        } else {
            System.out.println("Vertex \t Distance from Source");
            for (int i = 0; i < V; i++) {
                System.out.println(i + " \t\t " + (Integer.MAX_VALUE == edges[0].distance[i] ? "INF" : edges[0].distance[i]));
            }
        }
    }
}

4-3、 多源最短路径–Floyd-Warshall算法

Floyd-Warshall算法是解决任意两点间的最短路径的一种算法（）。 Floyd算法考虑的是一条最短路径的中间节点，即简单路径p={v1,v2,…,vn}上除v1和vn的任意节点。 设k是p 的一个中间节点，那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1，p2。p1是从i到k且中间节 点属于{1，2，…，k-1}取得的一条最短路径。p2是从k到j且中间节点属于{1，2，…，k-1}取得的一条最短路径。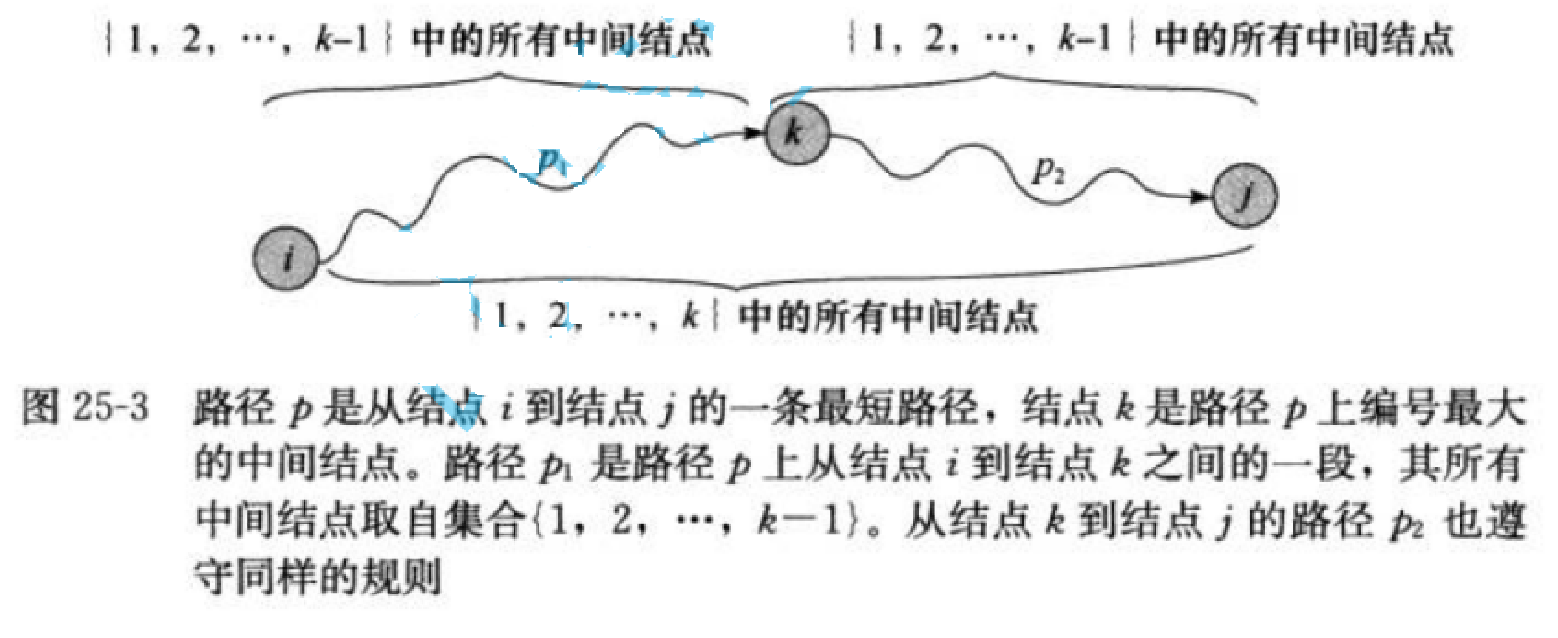

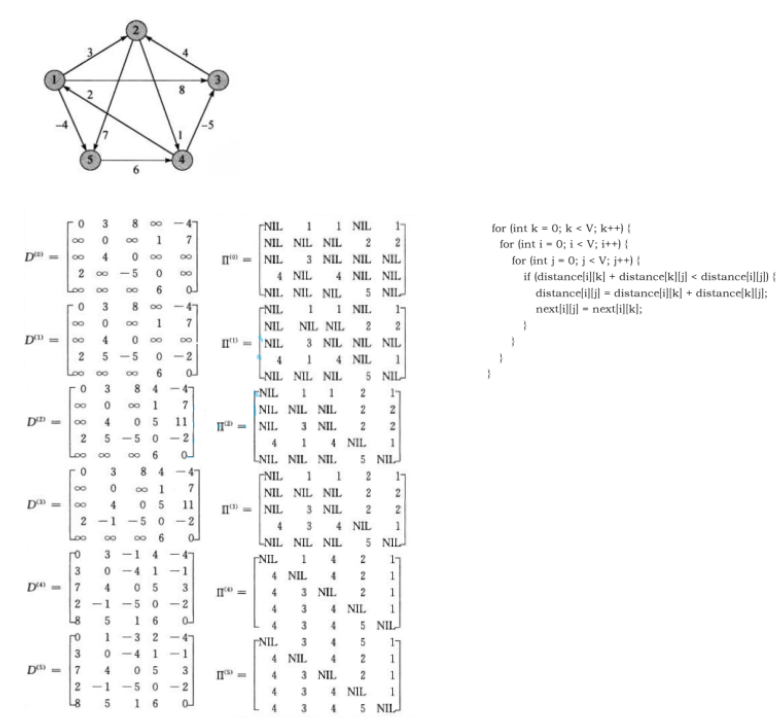
填表顺序不重要！填表不漏即可。

public void floydWarShall(int[][] dist,int[][] pPath) {
    int n = arrayV.length;

    for (int i = 0; i < n; i++) {
        Arrays.fill(dist[i],Constant.MAX);
        Arrays.fill(pPath[i],-1);
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if(matrix[i][j] != Constant.MAX) {
                dist[i][j] = matrix[i][j];
                pPath[i][j] = i;
            }else {
                pPath[i][j] = -1;
            }
            if(i == j) {
                dist[i][j] = 0;
                pPath[i][j] = -1;
            }
        }
    }

    for (int k = 0; k < n; k++) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if(dist[i][k] != Constant.MAX &&
                   dist[k][j] != Constant.MAX &&
                   dist[i][k] + dist[k][j] < dist[i][j]) {
                    dist[i][j] = dist[i][k] + dist[k][j];
                    //更新父节点下标
                    //pPath[i][j] = k;//不对
                    //如果经过了 i->k  k->j  此时是k
                    //i->x->s->k   k->..t->...x->j
                    pPath[i][j] = pPath[k][j];
                }
            }
        }
        // 测试 打印权值和路径矩阵观察数据
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if(dist[i][j] == Constant.MAX) {
                    System.out.print(" * ");
                }else{
                    System.out.print(dist[i][j]+" ");
                }
            }
            System.out.println();
        }
        System.out.println("=========打印路径==========");
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                System.out.print(pPath[i][j]+" ");
            }
            System.out.println();
        }
        System.out.println("=================");
    }
}

Floyd-傻子也能看懂的弗洛伊德算法