算法（读书笔记）：2.4优先队列

问题来源：

电脑或手机，通过为每个应用程序的事件分配一个优先级，并总是处理下一个优先级最高的事件来实现系统的调度。
这种情况下，合适的数据结构应该支持：
1.删除最大元素
2.插入元素

这种数据类型叫优先队列。
优先队列和队列（删除最老的元素）以及栈（删除最新的元素）类似。

基于此的排序：
通过插入一列元素然后一个个地删掉其中最小的元素，我们可以用优先队列实现排序。

堆排序：
来自于基于堆的优先队列的实现。

API：
优先队列是抽象数据类型，表示一组值和对这些值的操作。

abstract class MaxPQ<Key extends Comparable<Key>>{
    MaxPQ(){
    }//创建一个优先队列
    MaxPQ(int max) {
    }//创建一个优先队列,初始容量为max
    MaxPQ(Key[] a) {
    }//用a[]中元素创建一个优先队列
    void Insert(Key v) {
    }//插入一个元素
    Key max() {
        return null;
    }//返回最大元素
    Key delMax() {
        return null;
    }//删除并返回最大元素
    boolean isEmpty() {
        return false;
    }//返回优先队列是否为空
    int size() {
        return 0;
    }//返回优先队列中元素的个数
}

优先队列

应用场景：
输入N个字符串，每个字符串都对应着一个整数，从中找出最大的M个整数（及其关联的字符串）。在某些场景中，输入量巨大，可认为是无限的。
解决办法：
1.将输入排序然后从中找出M个最大元素。但已经说明输入非常大，这不可能。
2.将每个新的输入和已知的M个最大元素比较，但是除非M较小，否则这种比较的代价非常大。

考虑优先队列。只要维护有M个元素的优先队列，然后高效的实现insert和delMin方法就可以了！

从上图可以看出，优先队列只是抽象数据结构，真正怎样去实现，实现好坏直接跟性能挂钩。

优先队列的初级实现：
1.数组实现（无序）：
实现优先队列最简单方法是基于2.1节中下压栈的代码。insert方法的代码和栈的push完全一样。实现删除最大元素，可以添加一段类似于选择排序的内循环代码，将最大元素和边界元素交换然后删除它，和我们对栈的pop方法实现一样。
2.数组实现（有序）：
使数组保持有序。这样，最大的元素总会在数组的一边，优先队列的delMax就和栈的pop一样了。
3.链表表示法

使用无序序列是解决问题的惰性方法，只在必要的时候才会采取行动（找最大元素）。使用有序就比较积极，使后续更高效。

堆的定义：
数据结构二叉堆能够很好地实现优先队列的基本操作。

定义：当一颗二叉树的每个结点都大于等于它的两个子结点时，它被称为堆有序。
命题O：根结点是堆有序的二叉树中的最大结点。

二叉堆表示法：
若用指针来表示堆有序的二叉树，每个元素都需要三个指针（一个父结点，两个子结点）。
若使用完全二叉树，表达就会更简单。完全二叉树只用数组而不需要用指针就能表示。
具体做法：将二叉树的结点按照层级顺序放入数组中。根结点在位置1（完全是为了计算方便），它的子结点在2,3，以此类推。

定义：二叉堆是一组能够用堆有序的完全二叉树排序的元素，并在数组中按照层级存储（不使用数组的第一个位置，即0位）。
二叉堆是跟完全二叉树挂钩的。记住。

难点：在有序化过程中有两种情况：
1.当某个结点的优先级上升，需要上浮swim()。
2.当某个结点的优先级下降，需要下沉sink()。

//上浮实现
private void swim(int k){
        while(k>1&&less(k/2,k)){
            exch(k/2,k);
            k=k/2;
        }
    }
//下沉实现
private void sink(int k){
        while(2*k<=N){
            int j = 2*k;
            if(j<N&&less(j,j+1)) j++;//判断两个子结点哪个更大
            if(!less(k,j)) break;//若k优先级更大，不需要下沉
            exch(k,j);
            k=j;
        }
    }

sink()和swim()方法是高效实现优先队列API的基础。

思想：
1.插入元素。我们将新元素加到数组末尾，增加堆的大小，并让这个新元素上浮到合适的位置。
2.删除最大元素。我们从数组顶端删除最大元素并将数组的最后一个元素放到顶端，减小堆的大小并让这个元素下沉到合适的位置。（其实是两部，1删除，2维护堆有序性）

这里注意删除最大元素算法的思想。通过简单的将最后一个元素放在顶端维护了堆结构的完整性。

基于堆的优先队列的实现

//省略了动态调整数组大小的代码
class MaxPQ<Key extends Comparable<Key>>{
    private Key[] pq;//基于堆的完全二叉树
    private int N = 0;//数据存储于pa[1...N]中，pq[0]没有使用
    MaxPQ(int max) {
        pq = (Key[]) new Comparable[max+1];
        N = max;
    }//创建一个优先队列,初始容量为max
    void Insert(Key v) {
        pq[++N]=v;
        swim(N);
    }//插入一个元素
    Key max() {
        return pq[1];
    }//返回最大元素
    Key delMax() {
        Key max = pq[1];//从根结点得到最大元素
        exch(1,N--);//将其和最后一个结点交换
        pq[N+1]=null;//防止对象游离
        sink(1);//恢复堆有序
        return max;
    }//删除并返回最大元素
    boolean isEmpty() {
        return N==0;
    }//返回优先队列是否为空
    int size() {
        return N;
    }//返回优先队列中元素的个数

    private void swim(int k){
        //循环，直到位置对了为止
        while(k>1&&less(k/2,k)){
            exch(k/2,k);
            k=k/2;
        }
    }
    private void sink(int k){
        //循环，直到位置对了为止
        while(2*k<=N){
            int j = 2*k;
            if(j<N&&less(j,j+1)) j++;//判断两个子结点哪个更大
            if(!less(k,j)) break;//若k优先级更大，不需要下沉
            exch(k,j);
            k=j;
        }
    }
    private void exch(int i,int j){
        Key v = pq[i];
        pq[i] = pq[j];
        pq[j] = v;
    }
    private boolean less(int i,int j){
        return pq[i].compareTo(pq[j])<0;
    }
}

多叉堆：我们需要在树高(logdN)和在每个结点的d个子结点找到最大者的代价间折中，这取决于实现的细节以及不同的操作的预期相对频繁程度。

堆排序

堆排序分为两个阶段：
1.堆的构造阶段。将原始数组重新组织安排进一个堆中。
2.下沉排序阶段，我们从堆中按递减顺序取出所有元素并得到排序结果。

堆的构造：
由N个给定的元素构造一个堆。只需从左至右遍历数组，用swim保证扫描指针左侧的所有元素已经是一颗堆有序的完全数即可，就像连续向优先队列中插入元素一样。
但是，一个更聪明高效的方法是：从右至左用sink函数构造子堆。开始时，我们只需要扫描数组中的一半元素，因为我们可以跳过大小为1的子堆。
我们的目标是构造一个堆有序的数组并使最大元素位于数组的开头。

//堆排序，将堆中最大元素删除，然后放入堆缩小后数组空出的位置（也就是最后）
public void sort(Comparable[] a){
        //注意此时sink要传入N的值作为参数，因为N不变化的话，sink过程有可能又将数组末尾元素置换了
        int N = a.length;
        //有序堆的构造
        for (int i =N/2; i >=1; i--) {//从N的一半开始sink，因为下面的大小为1的堆不需要sink
            sink(i,N);
        }
        //完成数组的排序,使得数组递增，因为下面的逻辑是将最大值不断取出，放在数组末尾
        while(N>1){
            exch(1,N--);
            sink(1,N);
        }
    }

可视化：
一开始算法的行为似乎杂乱无章。因为随着堆的构建较大元素都被移动到了数组的开头，当接下来的算法的行为看起来和选择排序一模一样（除了它比较的次数比较少）。

堆排序在排序复杂性的研究中有着重要地位。
因为他是我们所知的唯一能够同时最优地利用空间和时间的方法—在最坏的情况下它也能保证使用2NlogN次比较和恒定的额外空间。

缺点：无法利用缓存！数组元素很少和相邻的其他元素进行比较，因此缓存未命中的次数要远远高于大多数比较都在相邻元素间进行的算法，如快排，归并排序，甚至是希尔排序。

另一方面，用堆实现的优先队列在现代应用中越来越重要，因为他能在插入操作和删除最大元素操作混合的动态场景中保证对数级别的运行时间。

排序应用总结

排序如此有用的原因：在一个有序的数组中查找一个元素要比在一个无序的数组中查找简单的多。比如电话簿。

我们使用的方法在经典教材中被称为指针排序，因为我们只处理元素的引用而不移动数据本身。
在java中，指针操作是隐式的。除了原始数据类型，我们操作的总是数据的引用（指针），而非数据本身。

多种排序方法：
在许多应用中，我们都希望根据情况将一组对象按照不同的方式排序。java的Comparator接口允许我们在一个类中实现多种排序方法。

Comparator接口允许我们为任意的数据类型定义任意多种排序方法。用Comparator接口来代替Comparable接口能够更好地将数据类型的定义和两个该类型的对象如何比较的定义区分开来，实现最大化的解耦。

//sort方法在每次比较中都会回调Transaction类中用例指定的compare方法。
    public static void sort(...,Comparator c){
        ...less(Comparator c,Object v,Object w);
    }
    private static boolean less(Comparator c,Object v,Object w){
        return c.compare(v, w)<0;
    }
class Transaction{
    private final String who;
    private final double amount;
    //不同的比较策略
    public static class WhoOrder implements Comparator<Transaction>{
        @Override
        public int compare(Transaction v, Transaction w) {
            return v.who.compareToIgnoreCase(w.who);
        }
    }
    public static class HowMuchOrder implements Comparator<Transaction>{
        @Override
        public int compare(Transaction v, Transaction w) {
            if(v.amount<w.amount) return -1;
            if(v.amount>w.amount) return +1;
            return 0;
        }
    }
}

稳定性：如果一个排序算法能够保留数组中重复元素的相对位置则可以被称为稳定的。但一般只有在稳定性是必要的情况下稳定的排序算法才有优势。

应该使用哪种排序算法：
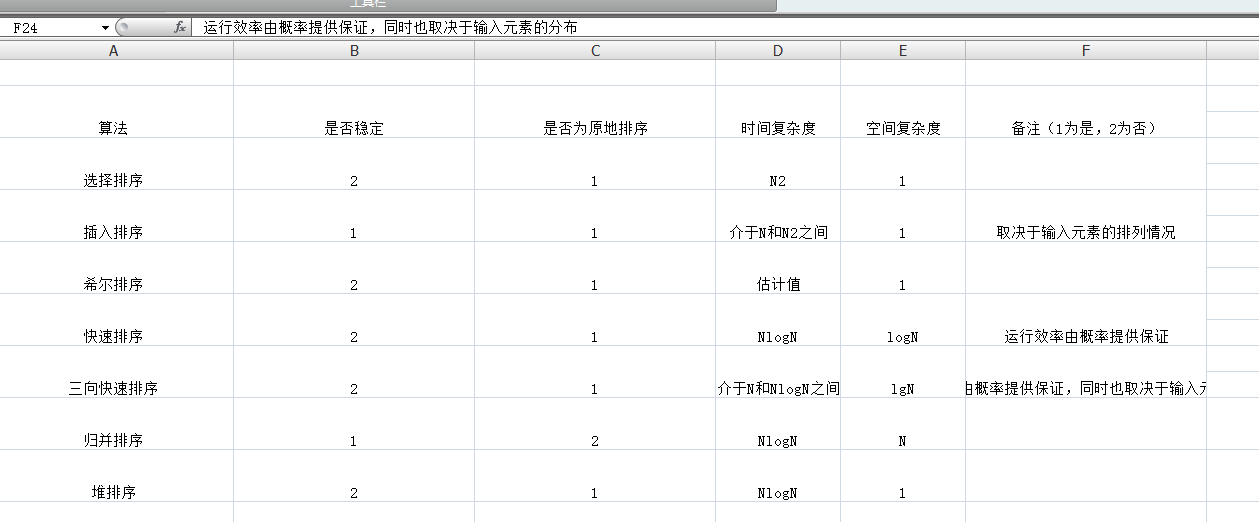
排序算法的好坏很大程度上取决于它的应用场景和具体实现，但我们也学习了一些通用的算法，他们能在很多情况下达到和最佳算法接近的性能。

性质T：快排是最快的通用排序算法。
在使用了三向切分以后，快排对于实际应用中可能出现的某些分布的输入变成线性级别的了，而其他的排序算法仍然需要线性对数级别。

java系统库的排序算法：
java系统程序员选择对原始数据类型使用（三向切分的）快速排序，对引用类型使用归并排序。这些选择是上暗示着速度和空间（对于原始数据类型）来换取稳定性（对于引用类型）。

问题的规约：
很多情况下如果先将数据排序，那么解决剩下的问题就只需要线性级别的时间了，这样规约后的运行时间的增长数量级就有平方级别降低到了线性对数级别。

课后问答：
问：java系统库中有优先队列这种数据类型吗？
答：有，见java.util.PriorityQueue。