专升本笔记记载-第六章-微分方程

微分方程

微分方程基本概念

微分方程定义

定义: 含有自变量x, 未知函数y(x), 及其导数y’, y’'(或 dy) 的等式叫做微分方程.

其中, 未知函数的导数(或微分)必须有, 而自变量x和未知函数y(x)可有也无.

例如:

​ y’ = 1 是微分方程

​ x + y’ = y 是微分方程

​ xdx + ydy = 0 是微分方程

​ x + y = 2 不是微分方程

常微分方程: 未知函数是一元函数的微分方程.

微分方程的阶

定义: 方程中未知函数导数的最高阶为方程的阶.

案例:

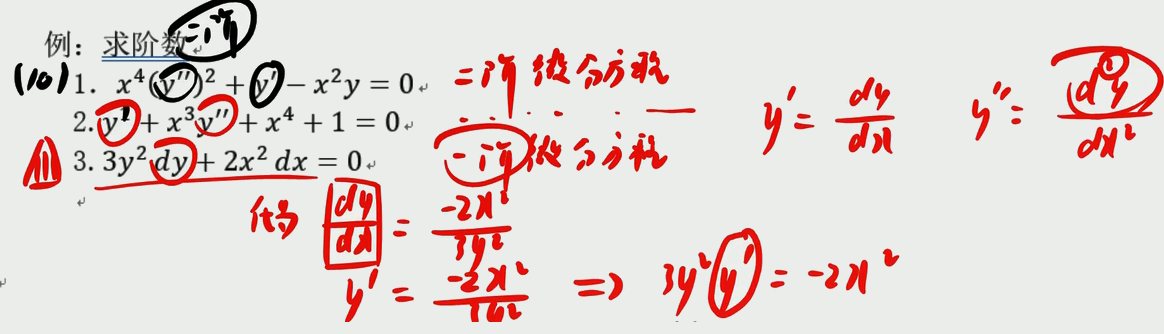
线性微分方程

非微分案例

在a与b中, 我们学习过的运算有:

1. 加减 (a+b)
2. 乘除 (a*b)
3. 数乘 (2*a)
4. 复合 (cosa, lna)

在这其中, 我们可以将其归类为:

​ 加减, 数乘 运算为线性运算.

​ 乘除, 复合 运算为非线性运算.

例如:

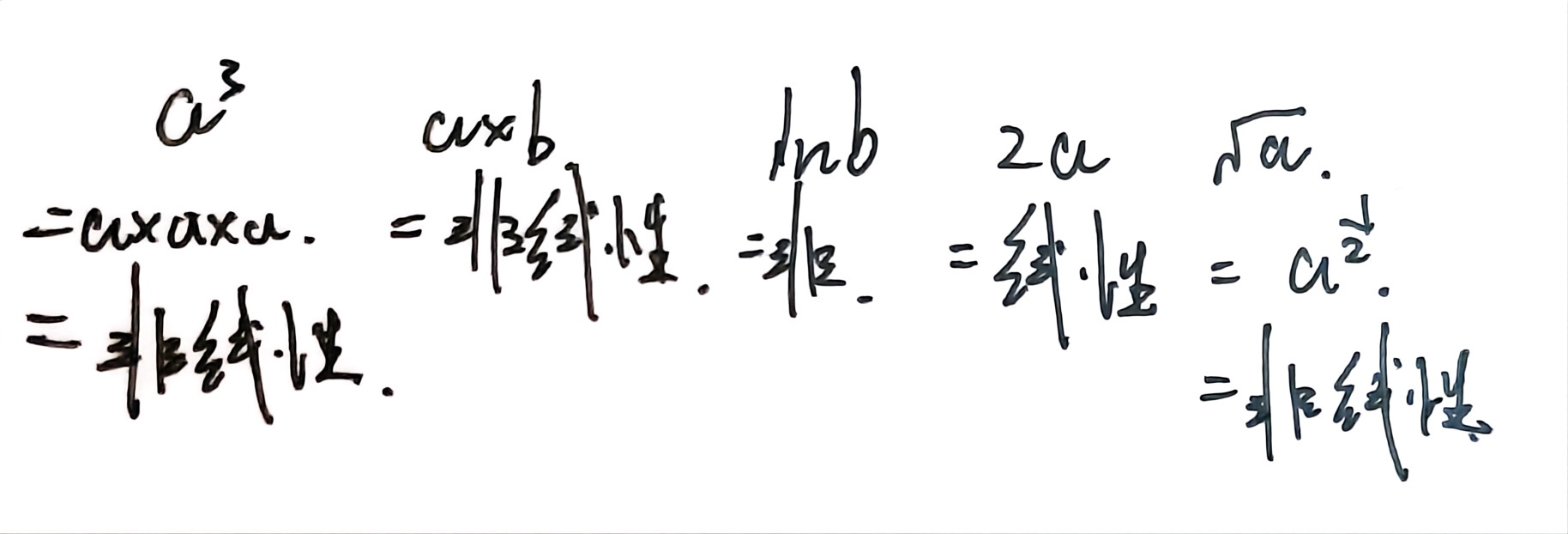
微分案例

线性微分方程的概念与案例如下:

主角是: y’ 以及 dy, 这里需要注意的是, y 是 y’ 的 0 阶导.

例题1&原因

微分方程的解

在这里我们先回顾一下中学所学习的代数方程, 通过代数方程来引入微分方程的概念.

代数方程: 含有 未知数x 的等式, 其解为数. 例如: x方 + 2x -3 = 0 的解是 x1=-3 以及 x2=1.

函数方程: 含有 未知函数y(x) 的等式, 其解为函数. 例如: x方 - y方 = 0 的解是 y = ±x

而微分方程是特殊的函数方程, 特殊在含有未知函数的导数. 微分方程的解也是函数.

---

代数方程 与 函数方程 解的特征: 把解代入到函数中, 可以使方程成立.

而微分方程中还存在两个解的类型, 分别如下:

1. 通解

   1. 含有相互独立的任意常数

      

   2. 任意常数的个数与方程阶数相同的解

2. 特解

   1. 不含任意常数的解

例题1&解法

例题2&解法

例题3&解法

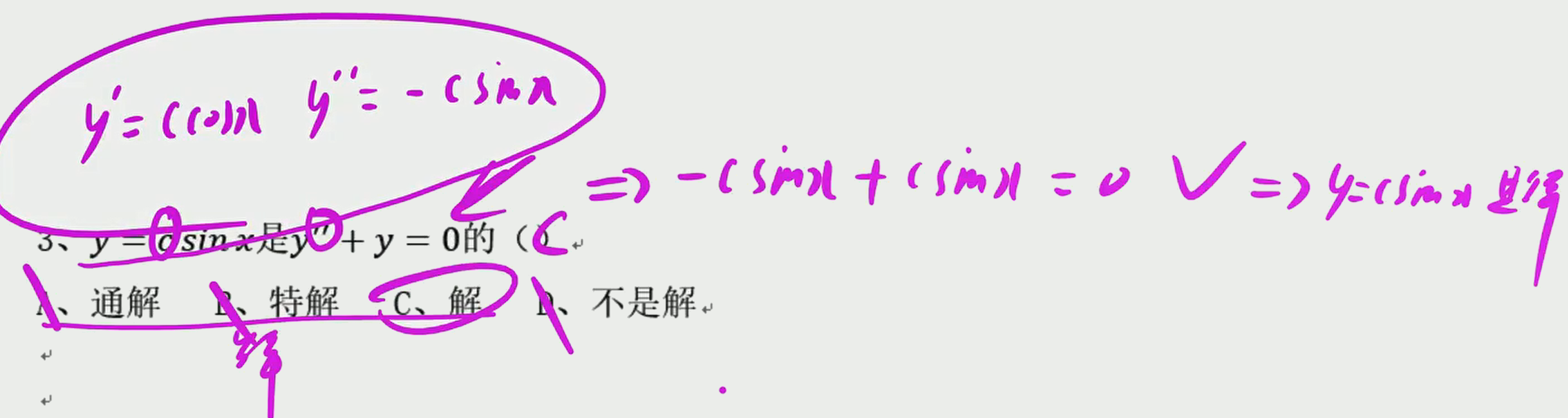
一阶微分方程

一阶可分离变量的微分方程 (熟练掌握)

判断方法

标准方程: f(x)dx = f(y)dy (课本中的理想状态) 例如: sinx·dx = lny·dy

题目中: y’=f(x)g(y), 方程可化为 y’ 在左边, 右边是纯x函数与纯y函数相乘/除的形式. 例如: y’=sinx·cosy

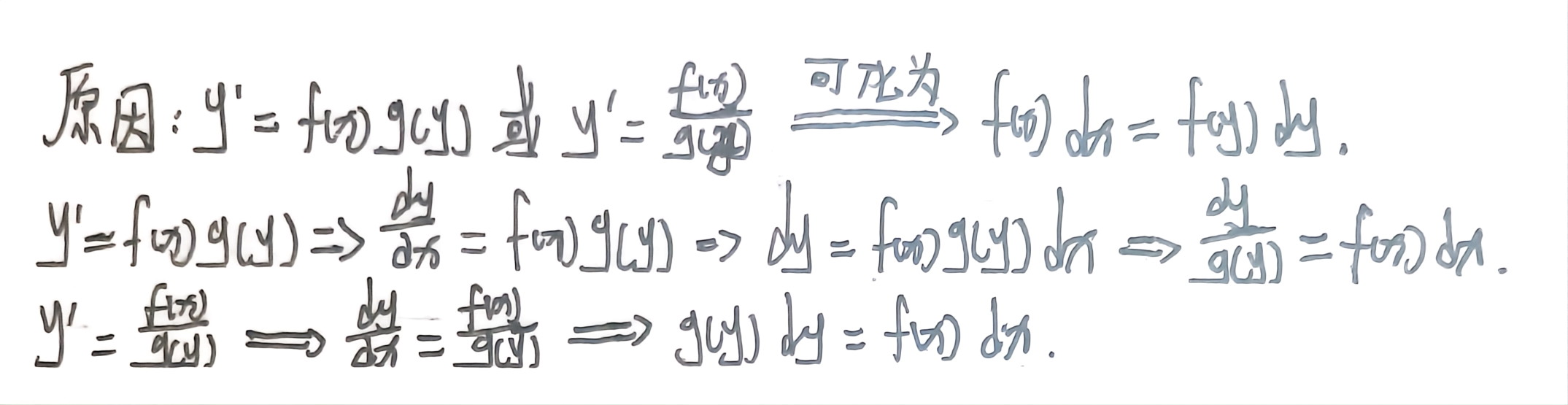
针对解法

1. 先将 y’ 放到等式左边, y’ = f(x)g(y) 或 y’ = f(x) / g(y) 右边是x函数与y函数相乘/除
2. 再将 y’ = f(x) / g(y) 化为 g(y)dy = f(x)dx 左边是y函数与dy, 右边是x函数与dx
3. 对 g(y)dy = f(x)dx 两边同时进行积分. 变为 ∫g(y)dy = ∫f(x)dx.

例题1&解法 (判断可分离变量)

例题2&解法 (判断可分离变量)

例题3&解法 (微分方程的通解)

例题4&解法 (微分方程的通解&特解)

一阶齐次微分方程 (不考)

一阶线性微分方程 (易考)

例题1&解法

高阶微分方程

可降价的高阶微分方程 (不考, 已忽略…)

…

二阶线性微分方程结构 (了解)

二阶常系数线性齐次微分方程 (熟练掌握)

二阶常系数线性非齐次微分方程

标准形式

y’’ + py’ + qy = f(x)

这里f(x)不等于0

知识储备

1. 知道二阶常系数线性非齐次方程可以推出二阶常系数线性齐次方程

   例如:

   ​ 非齐次:y'' + py' + qy = f(x) 可以推出 齐次: y'' + py' + qy = 0

2. 二阶常系数线性非齐次微分方程的通解 = 二阶常系数线性齐次微分方程的通解 + 二阶常系数线性非齐次微分方程的特解

   例如:

   ​ y’’ + 2y’ + 5y = 2x 的通解是多少？

   ​ y'' + 2y' + 5y = 0 的通解 + y'' + 2y' + 5y = 2x 的特解.

具体解法

1. 先求出对应齐次方程的通解Y.

2. 再求出非齐次方程的特解y`.

   特解形式: 通过设得到.

   然后将 特解形式 带入非齐次方程中, 将特解形式转化为特解.

3. 则, 非齐次方程的通解为 y = y` + Y

非齐次方程特解方法

第一种类型 (考通解与特解)

上面我们知道了如何设特解形式, 下面看一下如何进行通解.

例题2:

第二种类型 (只考特解形式)

几道例题:

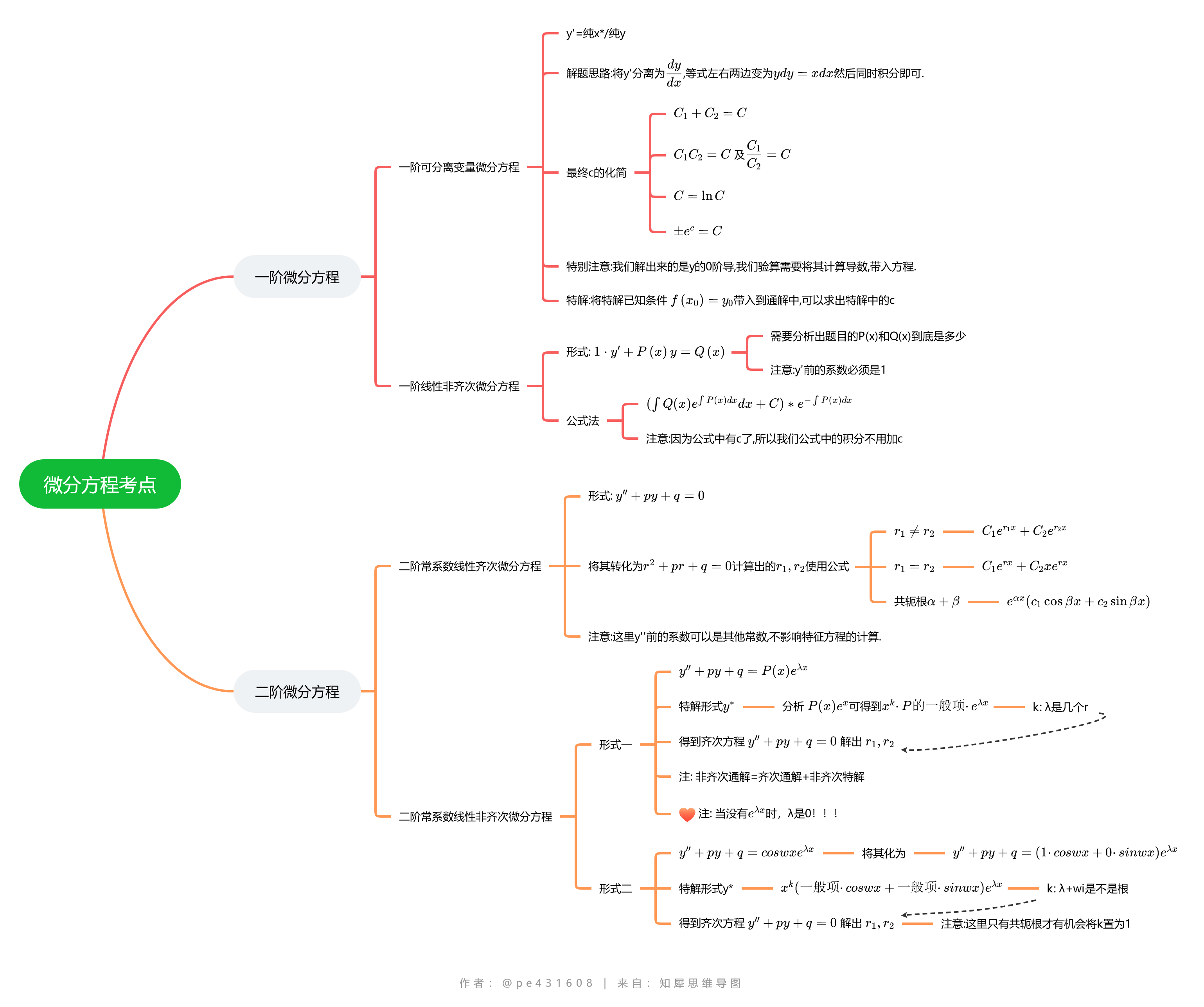
总结图片