错位排列——杨子曰数学
超链接:数学合集
首先,什么是错位排列?
就是你有1号物品,2号物品,3号物品……,它们都有自己对应的箱子:1号箱,2号箱,3号箱……
现在你把物品放到箱子里,结果一个物品也没有放对,全部都放错了,那么这个时候这些物品所构成的排列就被称为错位排列
接下来,我们来讨论错位排列怎么求,来简单推导一下错位排列总数的递推
我们用D[i]表示i个物品的错位排列总数
来看看D[n]怎么算,我们现在有n个物品,n个箱子:
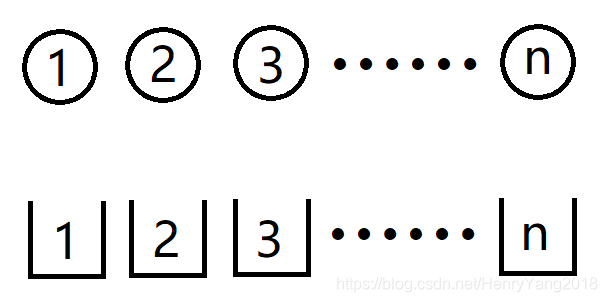
我们来考虑第1个物品,它只要不放到第一个箱子就行,So,有(n-1)种选择
比方说我们把它放到2号箱子
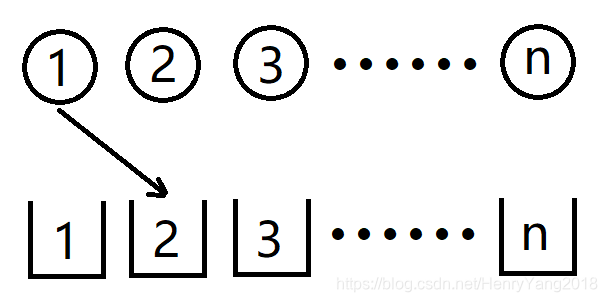
现在我们来考虑2号物品怎么处理
我们要进行分类讨论了
-
2号物品放到1号箱子
一旦把2号物品放到1号箱子中以后,有没有发现剩下的3~n号物品就是一个新的错位排列了
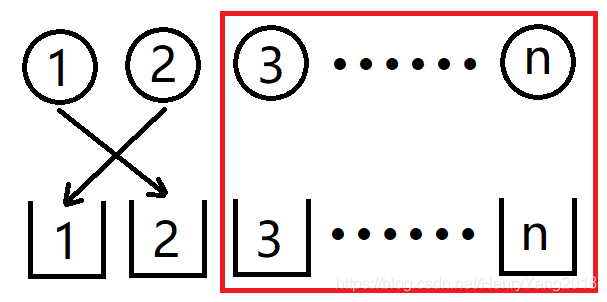
So,这种情况有D[n-2]种选法 -
2号物品不放到1号箱子
2号物品不能放到1号箱子,那么这时的1号箱子,就相当于问题最开始的2号箱子,都不能装2号物品
于是你有没有发现,红框里又是一个新的错位排列问题了
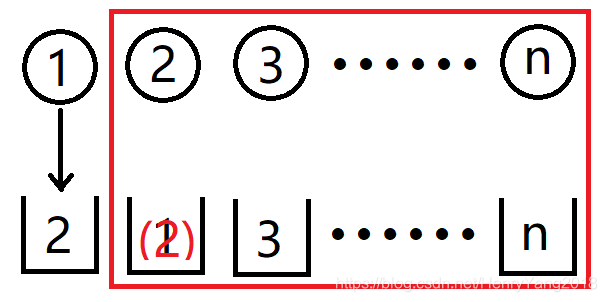
那么这种情况就有D[n-1]种选法了
然后1号物品除了放在2号箱子,还可以放在3号,4号……共(n-1)种选择
综上所述, D [ n ] = ( n − 1 ) ∗ ( D [ n − 1 ] + D [ n − 2 ] ) D[n]=(n-1)*(D[n-1]+D[n-2]) D[n]=(n−1)∗(D[n−1]+D[n−2])
一个小小的递推公式无法满足我们的要求,接下来我们来推导它的通项公式
D
[
n
]
=
(
n
−
1
)
∗
(
D
[
n
−
1
]
+
D
[
n
−
2
]
)
D[n]=(n-1)*(D[n-1]+D[n-2])
D[n]=(n−1)∗(D[n−1]+D[n−2])
⟹
D
[
n
]
(
n
−
1
)
!
=
D
[
n
−
1
]
(
n
−
2
)
!
+
D
[
n
−
2
]
(
n
−
2
)
!
\Longrightarrow\frac{D[n]}{(n-1)!}=\frac{D[n-1]}{(n-2)!}+\frac{D[n-2]}{(n-2)!}
⟹(n−1)!D[n]=(n−2)!D[n−1]+(n−2)!D[n−2]
令
N
[
n
]
=
D
[
n
]
n
!
则
n
∗
N
[
n
]
=
(
n
−
1
)
∗
N
[
n
−
1
]
+
N
[
n
−
2
]
令N[n]=\frac{D[n]}{n!}\ \ \ 则n*N[n]=(n-1)*N[n-1]+N[n-2]
令N[n]=n!D[n] 则n∗N[n]=(n−1)∗N[n−1]+N[n−2]
⟹
N
[
n
]
=
N
[
n
−
1
]
−
N
[
n
−
1
]
n
+
N
[
n
−
2
]
n
\Longrightarrow N[n]=N[n-1]-\frac{N[n-1]}{n}+\frac{N[n-2]}{n}
⟹N[n]=N[n−1]−nN[n−1]+nN[n−2]
⟹
N
[
n
]
−
N
[
n
−
1
]
=
−
1
n
∗
(
N
[
n
−
1
]
−
N
[
n
−
2
]
)
\Longrightarrow N[n]-N[n-1]=-\frac{1}{n}*(N[n-1]-N[n-2])
⟹N[n]−N[n−1]=−n1∗(N[n−1]−N[n−2])
令
H
[
n
]
=
N
[
n
+
1
]
−
N
[
n
]
则
H
[
n
−
1
]
=
−
1
n
∗
H
[
n
−
2
]
令H[n]=N[n+1]-N[n]\ \ \ 则H[n-1]=-\frac{1}{n}*H[n-2]
令H[n]=N[n+1]−N[n] 则H[n−1]=−n1∗H[n−2]
又
H
[
1
]
=
N
[
2
]
−
N
[
1
]
=
D
[
2
]
2
−
D
[
1
]
1
=
1
2
又H[1]=N[2]-N[1]=\frac{D[2]}{2}-\frac{D[1]}{1}=\frac{1}{2}
又H[1]=N[2]−N[1]=2D[2]−1D[1]=21
⟹
H
[
n
]
=
(
−
1
)
n
−
1
∗
1
(
n
+
1
)
!
\Longrightarrow H[n]=(-1)^{n-1}*\frac{1}{(n+1)!}
⟹H[n]=(−1)n−1∗(n+1)!1
⟹
N
[
n
]
−
N
[
n
−
1
]
=
H
[
n
−
1
]
=
(
−
1
)
n
∗
1
n
!
\Longrightarrow N[n]-N[n-1]=H[n-1]=(-1)^n*\frac{1}{n!}
⟹N[n]−N[n−1]=H[n−1]=(−1)n∗n!1
又
N
[
1
]
=
D
[
1
]
1
=
0
又N[1]=\frac{D[1]}{1}=0
又N[1]=1D[1]=0
⟹
N
[
n
]
=
1
2
!
−
1
3
!
+
⋯
+
(
−
1
)
n
∗
1
n
!
\Longrightarrow N[n]=\frac{1}{2!}-\frac{1}{3!}+\cdots+(-1)^n*\frac{1}{n!}
⟹N[n]=2!1−3!1+⋯+(−1)n∗n!1
⟹
D
[
n
]
=
n
!
∗
(
1
2
!
−
1
3
!
+
⋯
+
(
−
1
)
n
∗
1
n
!
)
\Longrightarrow D[n]=n!*(\frac{1}{2!}-\frac{1}{3!}+\cdots+(-1)^n*\frac{1}{n!})
⟹D[n]=n!∗(2!1−3!1+⋯+(−1)n∗n!1)
OK,完事
参考:
https://bubbleioa.blog.luogu.org/solution-p4071
于HG机房





















 216
216











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








