-
5 1 0 1 0 2 1 2 1 3 2 4 3
样例输出
3
这道题的难点在于如何找到从起点到其他节点的必经节点。然后想了好久,看了别人的讨论还是没太明白,百度到了一个题解,原来是有一个新的数据结构隐藏在这个里面——支配树。
先来谈谈什么叫支配树:什么是支配树?支配树是什么?XD
对于一张有向图(可以有环)我们规定一个起点r(为什么是r呢?因为网上都是这么规定的),从r点到图上另一个点w可能存在很多条路径(下面将r到w简写为r->w)。
如果对于r->w的任意一条路径中都存在一个点p,那么我们称点p为w的支配点(当然这也是r->w的必经点),注意r点不讨论支配点。下面用idom[u]表示离点u最近的支配点。
对于原图上除r外每一个点u,从idom[u]向u建一条边,最后我们可以得到一个以r为根的树。这个树我们就叫它“支配树”。简化问题:
树:对于一颗树,我们用r表示其根节点,那么从r->u上的点都是u的支配点,idom[u]就是u的父亲节点,这个很容易实现。
有向无环图:因为是有向无环图,所以我们可以用拓扑序列构建树。假设第x个节点是u,那么1-x-1的节点都已经处理好了,我们只需要把u节点的所有直接前驱的最近公共祖先找到即可。
解题思路:
·数据存储:
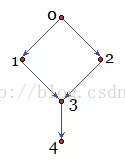
根据输入的成员信息,可以构建一个有向图来直观地表示成员之间的信息。此时Master和每一个成员分别用一个点来表示,当成员A是成员B的mentor时,点A到点B,之间就存在一条边。题目中给出的样例可以用下图来表示:这里用编号0来表示Master。此时,“不稳定成员”的定义就是:如果存在某一个编号不为0的点,使得从点0到该点的所有路径中都必须经过这个点,那么该点代表的成员就是“不稳定成员”。上图中,从点0到点4的所有路径必经过点3,因此成员4是不稳定成员。
支配树:
将上面“不稳定成员”的定义加以拓展,去掉“非0点”的限制,可以得到“支配点”的定义,即:对于某一个目标点,如果存在一个点,使得图中从起点到目标点所有路径都必须经过该点,那么该点就是目标点的“支配点”。上图中:点1、2、3、4的支配点分别为:0、0、0、0和3。显然,如果从起点出发可以到达图中的所有点,那么起点就是图中所有点的“支配点”。
一个点的“支配点”不一定只有一个。例如:如果对于某个点,从起点到该点的路径只有1条,那么该路径上的所有点都是该点的支配点。对于有多个支配点的情况,我们可以找到一个支配点,它距离目标点的最近,这个点我们成为“直接支配点”。对于给定的图,一个点可能用有多个支配点,但它的直接支配点一定是唯一的。此时,出去起点外,所有的点都有自己唯一的“直接支配点”。
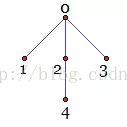
而“支配树”是这样的一种多叉树:图中的点对应于树的节点,而每一个节点的父节点则是它的直接支配点。上文中的图构成的支配树如下:显然,完成树的构建后,每个点的父节点就是它的直接支配点,而这个点的所有祖先节点都是它的支配点。此时,根据题意,我们要找的“稳定成员”就是直接支配点是0号点(Master)的成员,也就是支配树中根节点的孩子。
·建树:
为了建立支配树,就必须知道每个点的直接支配点。考虑原图中每个点的“前驱点”,本题中即考虑每个成员的mentor。如果某个成员只有一个mentor,那么显然从Master到该成员的路径一定都会经过他的mentor,因此mentor就是该成员的直接支配点;对于抽象的图而言,如果某一个点只有一个前驱点,那么该前驱点就是当前点的直接支配点;如果某个成员有多个mentor,那么对于某一个mentor而言,从Master到该成员就未必会经过它,所以,当某个成员拥有多个mentor时,他的mentor都不是他的直接支配点;对于抽象的图而言,如果一个点有多个前驱,那么这些前驱点都不是它的直接支配点,我们需要考虑这些前驱节点的支配点,当这些前驱节点拥有共同的一个支配点时,说明从起点到这些前驱点的所有路径必会经过这个共有的支配点,也就是说,从起点到目标点的所有路径都会经过这个共有的支配点,因此这个共有的支配点就是目标点的直接支配点。这个结论对于只有一个前驱节点的情况也使用
根据支配树的定义,多个节点共有的支配点是明确的,就是他们的公共祖先,而我们要找的则是最近公共祖先。这个结论对于只有一个前驱节点的情况也使用,因为如果只有一个点,那么它的最近公共祖先就是它自己。
于是,建立支配树的过程就是:首先将起点加入到树中,作为整个支配树的根,然后对于每一个节点,找到其所有前驱节点在支配树中的最近公共祖先,这个祖先节点就是当前节点的父节点。
·拓扑排序:
上面的建树过程有一个条件必须要保证,即某个点要加入到树中时,必须确保它的所有前驱点已经在树中,这样才可以找到这些点的最近公共祖先。因此,节点添加入树中的顺序是很重要的。我们可以通过拓扑排序找到合适的顺序,拓扑排序的结果就是节点加入树的顺序。这样就保证了前驱节点一定先于当前节点加入到树中。
·最近公共祖先:
建树的过程设计到了求多个节点的最近公共祖先。我们可以采用一种复杂度为O(lgn)的算法来求解它。考虑每个节点在树中的高度,将高度小的节点沿着父节点指针向上移动,在所有节点的高度相同时再同时沿着父节点指针向上移动,当所有的节点都到达同一个节点时,这个终点就是这些节点的最近公共祖先。
以上是本题的解答思路,完成建立支配树后,统计一下根节点有多少个孩子,就是本题的答案。
#include<iostream> #include<cstdio> #include<cstring> #include<queue> #include<vector> using namespace std; const int maxn = 100005; struct Edge { int to,next; }edge[maxn*10]; int n,cnt,ans,head[maxn],deg[maxn]; int dep[maxn],parent[maxn],tmp[15]; //tmp[i]表示第i个直接前驱回溯到的节点 vector<int> g[maxn]; void addedge(int u,int v) { edge[cnt].to = v; edge[cnt].next = head[u]; head[u] = cnt++; } int LCA(int u) { int min_dep = -1; for(int i = 0; i < g[u].size(); i++) { int v = g[u][i]; tmp[i] = v; if(min_dep == -1 || min_dep > dep[v]) min_dep = dep[v]; } for(int i = 0; i < g[u].size(); i++) { while(dep[tmp[i]] > min_dep) tmp[i] = parent[tmp[i]]; } while(true) { int i; for(i = 1; i < g[u].size(); i++) if(tmp[i] != tmp[0]) break; if(i >= g[u].size()) break; for(int i = 0; i < g[u].size(); i++) tmp[i] = parent[tmp[i]]; } return tmp[0]; } void bfs() { queue<int> q; for(int i = 0; i <= n; i++) if(deg[i] == 0) q.push(i); while(!q.empty()) { int u = q.front(); q.pop(); for(int i = head[u]; i != -1; i = edge[i].next) { int v = edge[i].to; deg[v]--; if(deg[v] == 0) { parent[v] = LCA(v); dep[v] = dep[parent[v]] + 1; if(parent[v] == 0) ans++; q.push(v); } } } } int main() { while(scanf("%d",&n)!=EOF) { memset(head,-1,sizeof(head)); memset(deg,0,sizeof(deg)); for(int i = 0; i <= n; i++) g[i].clear(); for(int i = 1; i <= n; i++) { int k; scanf("%d",&k); for(int j = 1; j <= k; j++) { int u; scanf("%d",&u); addedge(u,i); g[i].push_back(u); deg[i]++; } } ans = 0; bfs(); printf("%d\n",ans); } return 0; }
描述
Recently Little Hi joined an algorithm learning group. The group consists of one algorithm master and Nmembers. The members are numbered from 1 to N. Each member has one or more other members as his mentors. Some members' mentor is the master himself.
Every week each member sends a report of his own learning progress and the reports collected from his pupils (if there is any) to his mentors. The group is so well designed that there is no loop in the reporting chain so no one receives his own report from his pupil. And finally the master gets every one's report (maybe more than once).
Little Hi notices that for some members their reporting routes to the master can be easily cut off by a single member's (other than the master and himself) absence from the reporting duty. They are called unstable members while the others are stable members. Given the reporting network of the group, can you find out how many members are stable?
Assume there are 4 members in the group. Member 1 and 2 both have the master as their only mentor. Member 3 has 2 mentors: member 1 and member 2. Member 4 has 1 mentor: member 3. Then member 4 is the only unstable member in the group because if member 3 is absent his learning report will be unable to be sent to the master.
输入
The first line contains an integer N, the number of members.
The i-th line of the following N lines describe the mentors of the i-th member. The first integer is Ki, the number of mentors of the i-th member. Then follows Ki integers A1 ... AN, which are his mentors' numbers. Number 0 indicates that the master is one of his mentor.
For 40% of the data, 1 ≤ N ≤ 1000.
For 100% of the data, 1 ≤ N ≤ 100000.
For 100% of the data, 1 ≤ Ki ≤ 10, Ki < N, 0 ≤ Ai ≤ N.
输出
Output the number of stable members.






















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








