【C++】AVL树

最新推荐文章于 2024-06-15 16:46:40 发布

INsisting..

最新推荐文章于 2024-06-15 16:46:40 发布

阅读量327

点赞数

分类专栏： C++ 数据结构文章标签： c++ 算法

本文链接：https://blog.csdn.net/hhjjjx/article/details/132875072

版权

C++ 同时被 2 个专栏收录

6 篇文章 0 订阅

订阅专栏

数据结构

3 篇文章 0 订阅

订阅专栏

一、AVL树的定义

AVL树，全称 平衡二叉搜索（排序）树。

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

平衡因子（Balance Factor，简写为bf）
平衡因子（bf）：结点的左子树的深度减去右子树的深度。也可以是右子树的深度减去左子树的深度。看个人实现而异。

即： 结点的平衡因子 = 左子树的高度 - 右子树的高度。
或者 节点的平衡因子 = 右子树的高度 - 左子树的高度。

AVL树本质上是一颗二叉查找树，但是它又具有以下特点：

它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

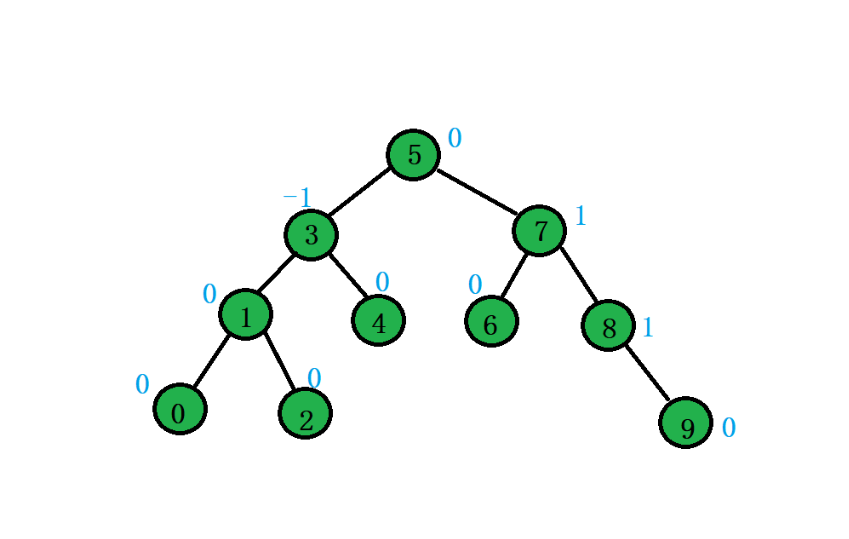
这就是一颗AVL树

二、AVL树的作用

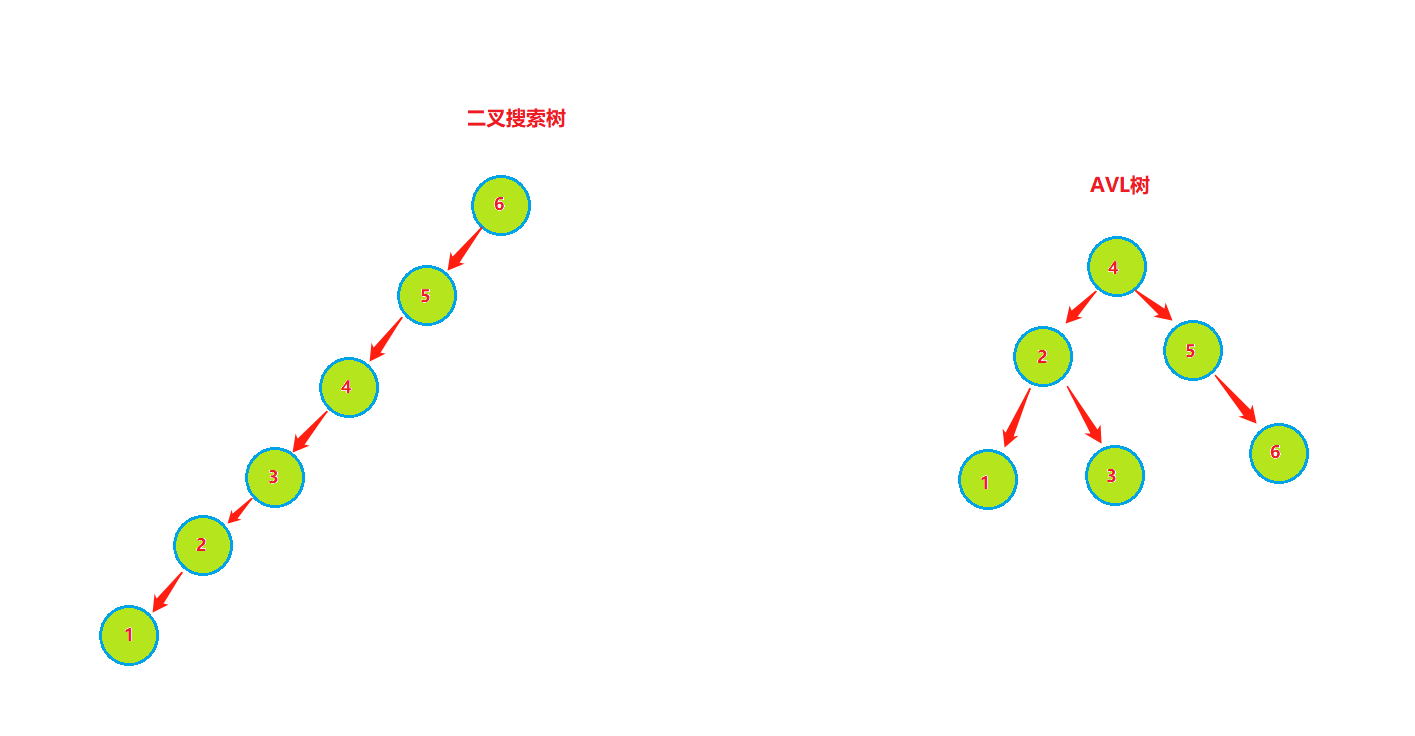
有一颗二叉树，他有n个节点，如果他是一颗二叉搜索树，他形状多样，可能会形成单枝树，高度为n,那么在这颗搜索树中查找元素的最坏时间复杂度为O(n),最好时间复杂度是O( $log_2 n$ )。
如果他是一颗AVL树，他的高度稳定为 $log_2 n$ ,查找元素的时间复杂度为O( $log_2 n$ )。
由上图可知，同样的结点，由于插入方式不同导致树的高度也有所不同。特别是在带插入结点个数很多且正序的情况下，会导致二叉树的高度是O(N)，而AVL树就不会出现这种情况，树的高度始终是O(lgN).高度越小，对树的一些基本操作的时间复杂度就会越小。这也就是我们引入AVL树的原因。

三、AVL树的插入操作

插入——平衡因子的更新

在插入一个元素的时候，必然会引起平衡因子的变化，所以我们需要在插入的时候把平衡因子同时更新，在平衡因子大于1或者小于-1时，我们则需要进行旋转操作，进行调整，使平衡因子再次正常，从而保证这颗二叉树一直是一颗AVL树。

使用平衡因子计算：右子树高度 - 左子树高度

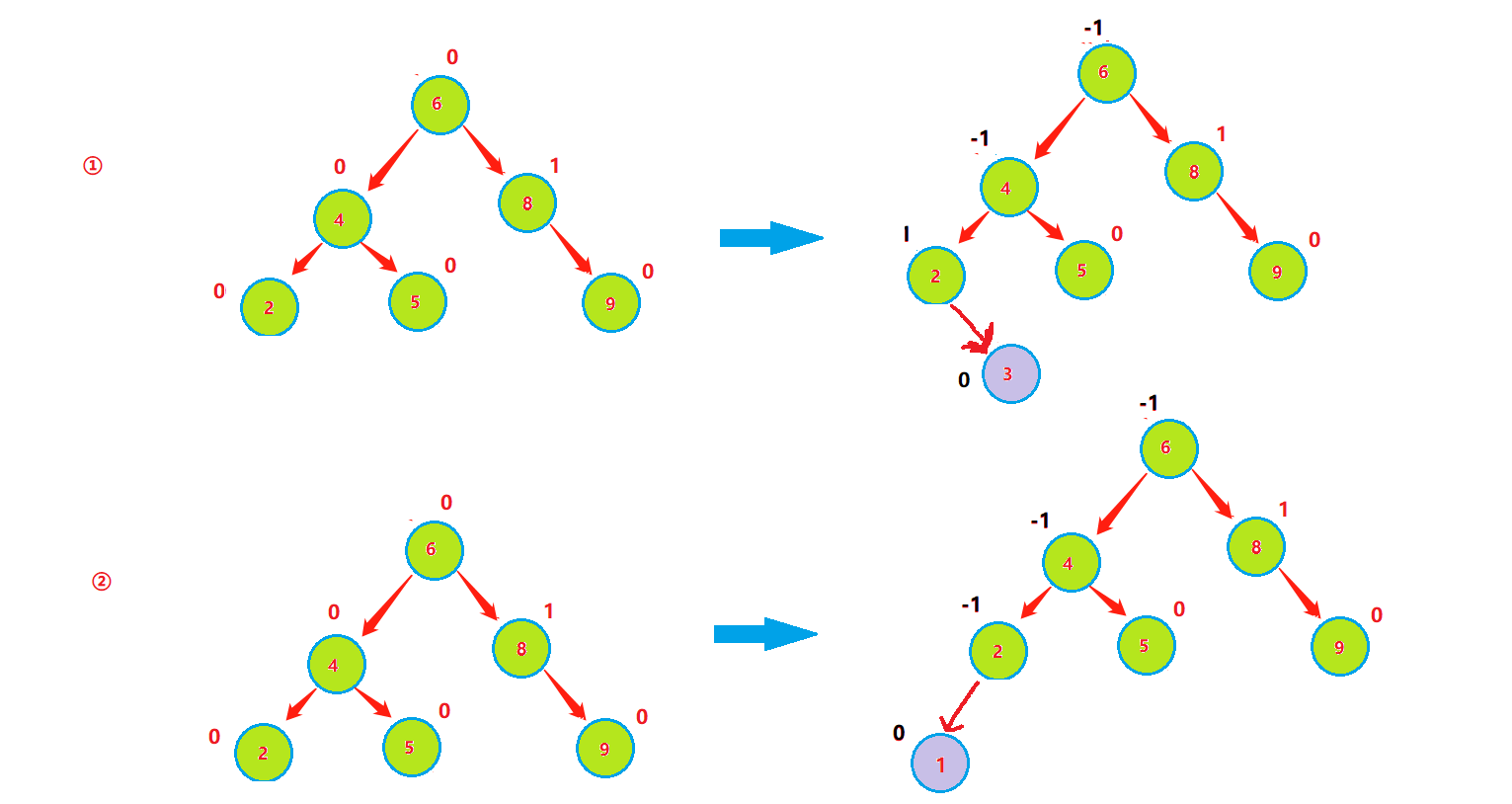
情况一：

在插入元素后，需要更新父节点的平衡因子，在父节点的左子树插入元素，父节点的平衡因子-1，在父节点的左子树插入元素，父节点的平衡因子+1，如果父节点的平衡因子更新过后变为1或者-1，则需继续往上更新至根节点，因为1或者-1表示该节点的高度发生改变，需往上更新。

情况2：

在插入元素后，需要更新父节点的平衡因子，在父节点的左子树插入元素，父节点的平衡因子-1，在父节点的左子树插入元素，父节点的平衡因子+1，如果父节点的平衡因子更新过后变为0，则不需要继续向上更新，因为变为0只能说明该树高度没有变化，只是相对于原来变得平衡。

如果在更新平衡因子后，平衡因子不在(-1/0/1)范围时，则需旋转操作，下面讲解如何进行旋转操作

由于插入需要旋转的情况较多，大致可以分为四大类

插入——左单旋

动图演示
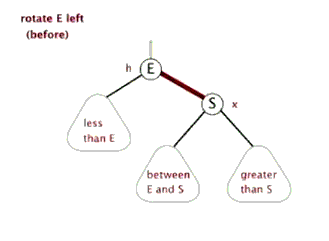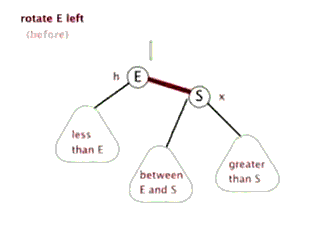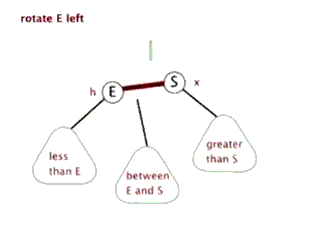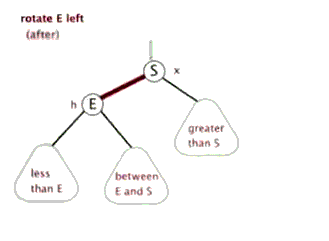
请添加图片描述

情况一
右子树高时，在右子树的右侧插入元素，此时需要左单旋

插入——右单旋

动图演示
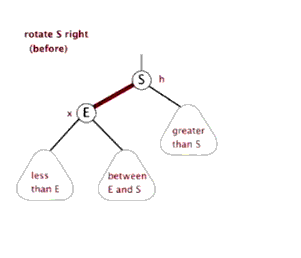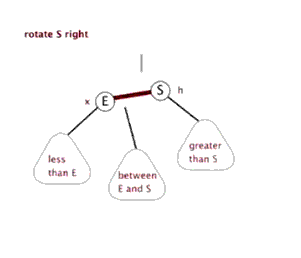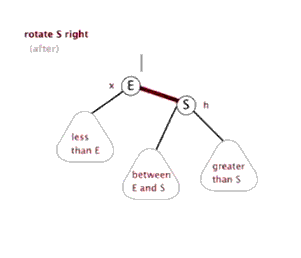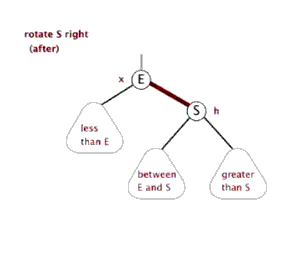
请添加图片描述

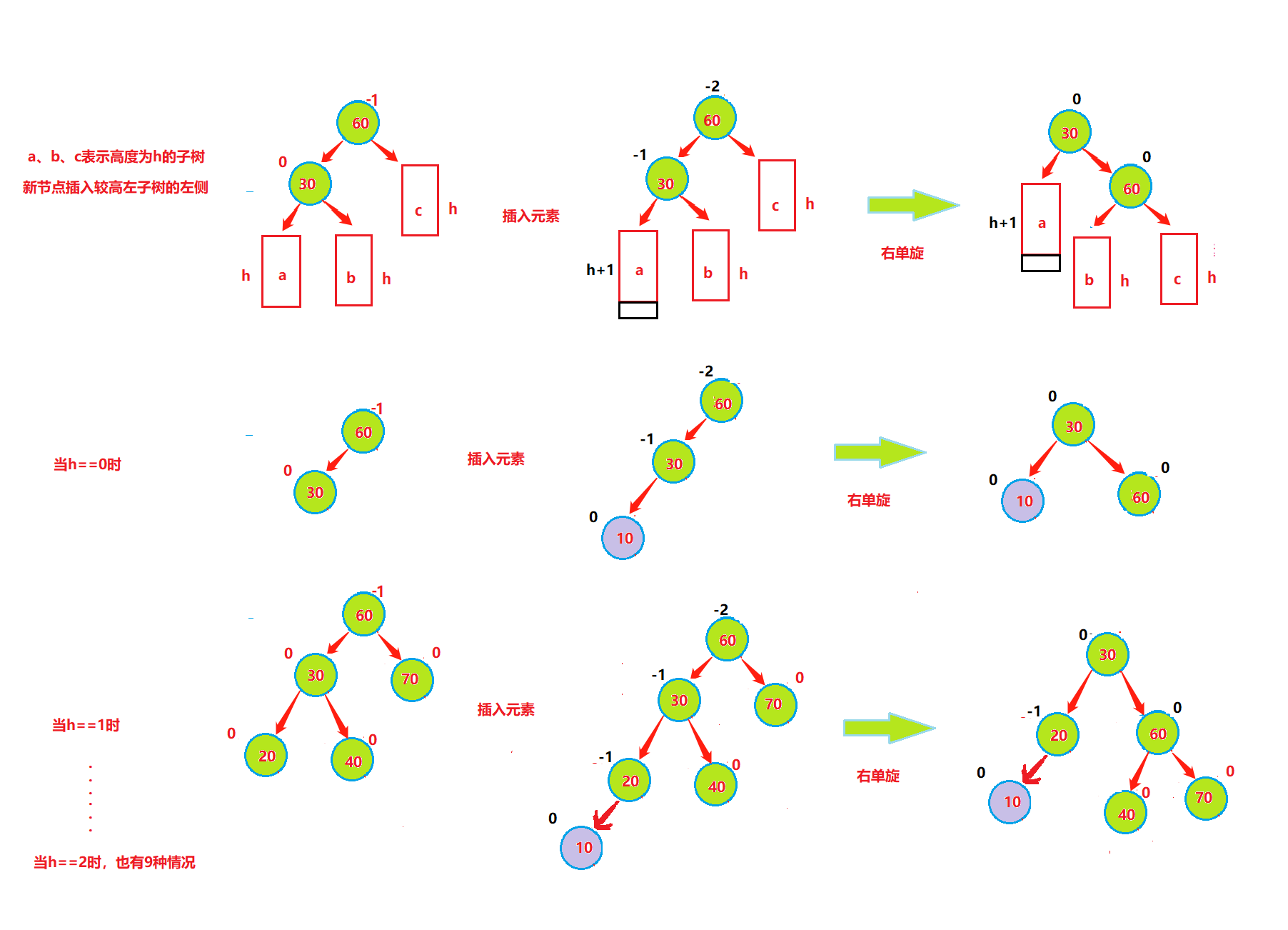
情况二、
左子树较高时，在左子树的左侧插入元素，此时需要右单旋

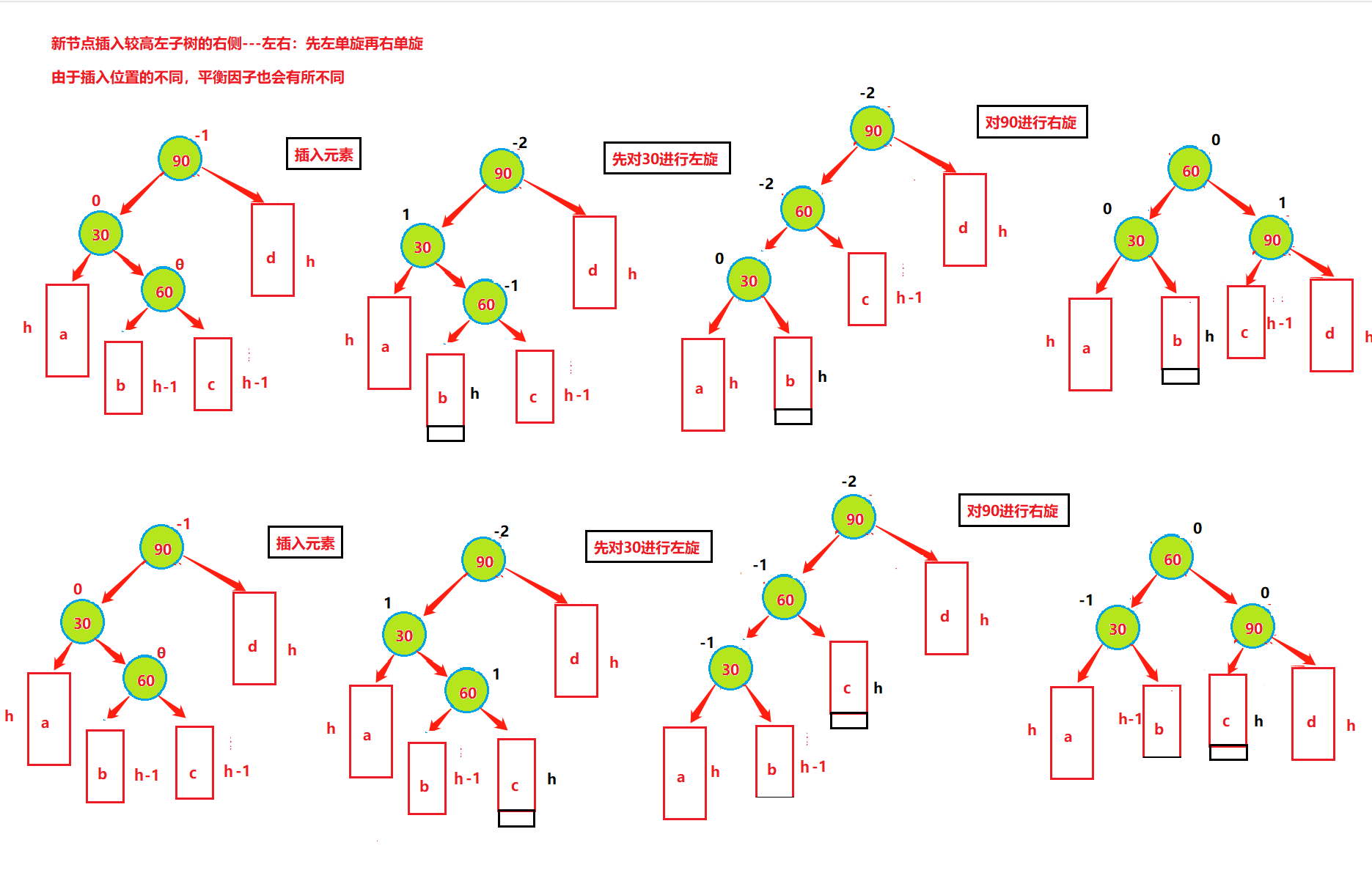
插入——左右双旋

情况三、左子树较高时，在左子树的右侧插入元素，此时需要左右双旋，即：先对30进行左单旋，然后再对90进行右单旋

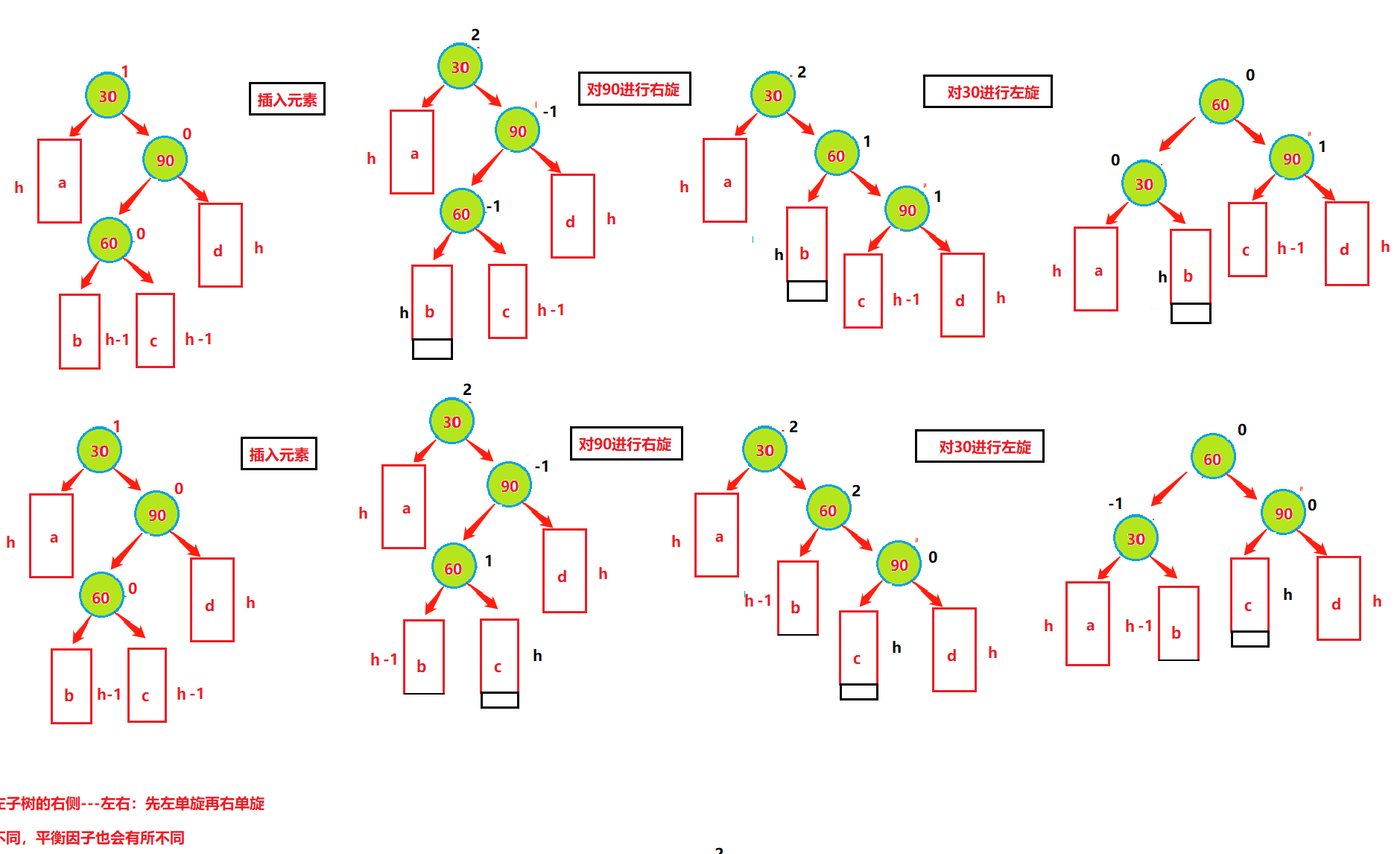
插入——右左双旋

情况四、右子树较高时，在右子树的左侧插入元素，此时需要右左双旋，即：先对90进行右单旋，然后再对30进行左单旋

四、ALVL树的验证

int _Height(Node* root)
{
	//用来计算二叉树的高度
	if (root == NULL)
		return 0;
	int leftH = _Height(root->_left);
	int rightH = _Height(root->_right);
 
	return leftH > rightH ? leftH + 1 : rightH + 1;
}
 
bool _IsBalance(Node* root)
{
	if (root == NULL)
		return true;
	int leftH = _Height(root->_left);
	int rightH = _Height(root->_right);
 	
 	//检查平衡因子
	if (rightH - leftH != root->_bf)
	{
		cout << root->_kv.first << "节点平衡因子异常" << endl;
		return false;
	}
 	//通过计算左右子树的高度差判断这颗二叉树是否为AVL树
	return abs(leftH - rightH) < 2
		&& _IsBalance(root->_left)
		&& _IsBalance(root->_right);
		//检查高度差要检查二叉树中所有节点的左右子树的高度差
}
 
bool IsBalance()
{
	return _IsBalance(_root);
}

五、AVL树的性能

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即 $log_2 n$ 。

但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。

六、代码

#pragma once
#include<iostream>

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K,V>* _left;
	AVLTreeNode<K,V>* _right;
	AVLTreeNode<K,V>* _parent;
	pair<K,V> _kv;
	int _bf; // blance factor

	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			//根节点为空，创建一个节点为根节点
			_root = new Node(kv);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kv.first< cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else return false;    //要插入的元素已经存在，返回 false
		}

		cur = new Node(kv);
		if (cur->_kv.first < parent->_kv.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		//更新平衡因子  右 - 左
		while (parent)
		{
			if (cur == parent->_right)
			{
				parent->_bf++;
			}
			else if (cur == parent->_left)
			{
				parent->_bf--;
			}

			if (parent->_bf == 1 || parent->_bf == -1)
			{
				//继续更新
				parent = parent->_parent;
				cur = cur->_parent;
			}
			else if (parent->_bf == 0)break;
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//调整  旋转   1.让这颗子树平衡  2.降低这颗子树的高度
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					//左单旋
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					//右单旋
					RotateR(parent); 
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);
				}

				break;
			}
		}
		return true;
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
	bool IsBalance()
	{
		//判断平衡
		return _IsBalance(_root);
	}
private:
	int _Height(Node* root)
	{
		//计算二叉树的高度
		if (root == NULL)return 0;
		int leftH = _Height(root->_left);
		int rightH = _Height(root->_right);

		return leftH > rightH ? leftH + 1 : rightH + 1;
	}
	bool _IsBalance(Node* root)
	{
		if (root == NULL)return true;
		
		int leftH = _Height(root->_left);
		int rightH = _Height(root->_right);

		if (rightH - leftH != root->_bf)  //检查平衡因子
		{
			cout << root->_kv.first << "节点平衡因子异常" << endl;
		}
		//需要遍历所有节点检查高度差
		return abs(leftH - rightH) < 2 
			&&_IsBalance(root->_left)
			&&_IsBalance(root->_right);
	}
	void RotateL(Node* parent)  //左单旋
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)subRL->_parent = parent; //subRL可能为空

		Node* ppnode = parent->_parent;

		subR->_left = parent;    //parent节点成为subR的左子树节点
		parent->_parent = subR;

		
		if (ppnode == nullptr)  //判断当前传入的节点是否为根节点
		{
			_root = subR;
			_root->_parent = nullptr;
		} 
		else {
			if (ppnode->_left == parent)
			{
				ppnode->_left = subR;
			}
			else {
				ppnode->_right = subR;
			}
			subR->_parent = ppnode; //subR 成为当前子树的根节点
		}
		parent->_bf = subR->_bf = 0; //旋转后更新平衡因子
	}

	void RotateR(Node* parent) //右单旋
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)subLR->_parent = parent;

		Node* ppnode = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (ppnode == nullptr)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (parent == ppnode->_left)
			{
				ppnode->_left = subL;
			}
			else {
				ppnode->_right = subL;
			}
			subL->_parent = ppnode;
		}
		parent->_bf = subL->_bf = 0;
	}
	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == 1)
		{
			parent->_bf = 0;
			subLR->_bf = 0;
			subL->_bf = -1;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subLR->_bf = 0;
			subL->_bf = 0;
		}
		else if (bf == 0) //特殊情况
		{
			parent->_bf = 0;
			subLR->_bf = 0;
			subL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}
	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 1)
		{
			parent->_bf = -1;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 1;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)return;

		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}
	

private:
	Node* _root = nullptr;
};

void Test_AVLTree1()
{
	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16,14 };
	AVLTree<int, int> t1;
	for (auto e : a)
	{
		t1.Insert(make_pair(e,e));
	}
	
	t1.InOrder();
	cout << t1.IsBalance() << endl;
}

void Test_AVLTree2()
{
	srand(time(0));
	const size_t N = 10000;
	AVLTree<int, int> t;  //插入10000个数据
	for (size_t i = 0; i < N; ++i)
	{
		size_t x = rand();
		t.Insert(make_pair(x, x));
	}
	cout << t.IsBalance() << endl;
}

INsisting..

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
1
评论
【C++】AVL树

AVL树，全称平衡二叉搜索（排序）树。二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。平衡因子（Balance Factor，简写为bf）
复制链接

扫一扫