模式分类笔记 -- 统计学习（1）

一个linear threshold gate (LTG)可以用来把向量输入映射到二进制输出。

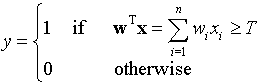
以太泛化的模型或情况来讨论只能掩盖其初始的动机和灵光。Treating a more general case will only obscure the basic ideas.

如果我们考虑这样的一个方程，y(x1, x2, x3) = x1'x2 + x2x3'(这里用‘来表示求反)， x1，x2, x3取【0，1】。

那么三个变量就有2的3次方种组合，那么对于n个变量，则存在 m=2的n次方 个组合，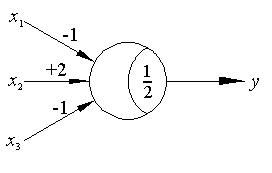

当然这里n都是些二元变量，存在着2的m次方个不同的方式来把这m种组合标记成两种

不同的类别。又是一种排列组合。这个boolean function是线性可分的，例如右面这个

LTG实现，当然这个LTG只是众多可以用来完成划分的LTG中的一个。

一个单独的n维输入LTG只能表达这2的m次方个布尔方程的一个小子集 。能够被LTG表达的布尔方程是线性可分系统。比如说异或问题就不是线性可分的，这样的布尔方程成为non-threshold方程，反之就是threshold方程。当n->无穷时，能被threshold function表示的布尔方程与全体布尔方程的比值的极限等于0.这点我们可以从下面的自由度之比看出来。

有些逻辑门是可以被LTG表示的，比如说NAND (or NOR)，这说明LTG也是一个普遍的逻辑门，any Boolean function is realizable using a network of LTG's (only two logic levels are needed)。除了NAND (or NOR)， LTG还能实现一些更复杂的逻辑门，因此一个n输入的LTG比n输入的NAND (or NOR)更加powerful 。

 

考虑到很大的n时，线性可分性比例很小，所以我们应尝试设计一些更加powerful的逻辑门来实现non-threshold function,这可以通过扩展LTG的输入来实现 ，比如我们可以提供输入的积（products）或者与（andings）作为新输入提供给LTG，这显然就已经破坏了线性形式，：）。在这种情况下，我们需要一个固定的预处理与门层来增加输入空间的维度，我们期望这个新boolean function变成一个thershold function, 那么他就可以用一个LTG实现。这样QTG诞生了。

 

Quadratic Threshold Gates（QTG）：

 

    

 

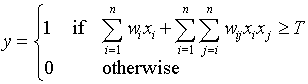
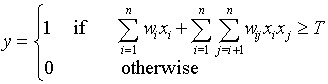
x属于实数域和布尔域的时候，double summation term中index j 的范围不一样，首先他们都把xixj与xjxi（i<>j）看作一项,另外你发现在boolean域，把xixj（i = j）这项在后面也排除掉了，这是因为布尔域里xi *xi = xi, xi项在前面的一阶多项式里已经出现了。

 

 

LTG与QTG的自由度（参数数目）对比表格。

Threshold gate	Number of degrees of freedom/parameters (including threshold -- 就是多项式里的b)
LTG	n + 1
QTG

 

上面的QTG自由度就是简单的加加就出来了，贴在那里貌似很突兀。

 

我们可以看到产生的booleanfunction自由度（parameter）的数目明显增大,我们继而推广到Polynomial Threshold

Gates（PTG），PTG变成了一个很强大的门（gate）。

 

 

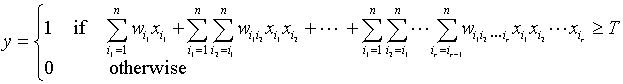
PTG的自由度：

 

        

 

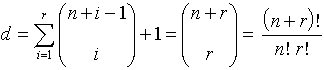
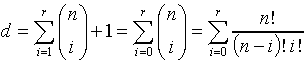
表示m个点中每个取k时组合的数目，方便的记法而已。