1.前言:数字信号处理相关知识准备
通常来说,一种理想滤波器的频率响应是很容易理解的,如图所示。

图1 滤波器频响
以低通为例,滤波器频率响应函数为
 。
。
所谓滤波器处理的过程,简单来说,可以用公式

来表示,由卷积的性质可以知道,该公式的另一种形式为
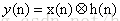
其中x(n)为要处理的数据序列,h(n)为逼近滤波器的时域响应
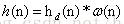
其中,hd(n)为对应不同类型滤波器的单位冲击响应,比如说低通的hd(n)为sinc函数。
我们知道,高通可以有全通减低通得到,带通可由两个低通相减得到,带阻可由低通加高通得到。
2. 具体VC实现过程
有了上面简单的回顾之后,我们就可以进行VC上滤波器的实现了。首先是hd(n)的实现,具体代码如下:
头文件声明部分
#pragma once
class CFIRWIN
{
public:
CFIRWIN(void);
~CFIRWIN(void);
void firwin(int n,int band,int wn,double h[],double kaiser=0.0,double fln=0.0,double fhn=0.0);
double window(int type,int n,int i,double beta);//窗函数的计算
double kaiser(int i,int n,double beta);
double bessel0(double x);
};
源文件实现部分
#include "StdAfx.h"
#include "FIRWIN.h"
#include <math.h>
CFIRWIN::CFIRWIN(void)
{
}
CFIRWIN::~CFIRWIN(void)
{
}
void CFIRWIN::firwin(int n,int band,int wn,double h[],double kaiser,double fln,double fhn)
{
int i,n2,mid;
double s,pi,wc1,wc2,beta,delay,fs;
fs=44100;//44kHz
beta=kaiser;
pi=4.0*atan(1.0);//pi=PI;
if((n%2)==0)/*如果阶数n是偶数*/
{n2=n/2+1;/**/
mid=1;//
}
else
{n2=n/2;//n是奇数,则窗口长度为偶数
mid=0;//
}
delay=n/2.0;
wc1=pi*fln;//
if(band>=3) wc2=pi*fhn;/*先判断用户输入的数据,如果band参数大于3*/
switch(band)
{case 1:
{for(i=0;i<=n2;i++)
{s=i-delay;//
h[i]=(sin(wc1*s/fs)/(pi*s))*window(wn,n+1,i,beta);//低通,窗口长度=阶数+1,故为n+1
h[n-i]=h[i];
}
if(mid==1) h[n/2]=wc1/pi;//n为偶数时,修正中间值系数
break;
}
case 2:
{for(i=0;i<n2;i++)
{s=i-delay;
h[i]=(sin(wc2*s/fs)-sin(wc1*s/fs))/(pi*s);//带通-//对
h[i]=h[i]*window(wn,n+1,i,beta);
h[n-i]=h[i];
}
if(mid==1)h[n/2]=(wc2-wc1)/pi;//对
break;
}
case 3:
{for(i=0;i<=n2;i++)
{s=i-delay;
h[i]=(sin(wc1*s/fs)+sin(pi*s)-sin(wc2*s/fs))/(pi*s);//带阻-//对
h[i]=h[i]*window(wn,n+1,i,beta);
h[n-i]=h[i];
}
if(mid==1)h[n/2]=(wc1+pi-wc2)/pi;
break;
}
case 4:
{ for(i=0;i<=n2;i++)
{s=i-delay;
h[i]=(sin(pi*s)-sin(wc1*s/fs))/(pi*s);//高通-//对
h[i]=h[i]*window(wn,n+1,i,beta);
h[n-i]=h[i];
}
if(mid==1) h[n/2]=1.0-wc1/pi;//对
break;
}
}
// for (int _i=0;_i<n+1;_i++)
// {
// h[_i]*=(double)(n+1);
// }
}
double CFIRWIN::window(int type,int n,int i,double beta)
{
int k;
double pi,w;
pi=4.0*atan(1.0);//pi=PI;
w=1.0;
switch(type)
{case 1:
{w=1.0;//矩形窗
break;
}
case 2:
{k=(n-2)/10;
if(i<=k)
w=0.5*(1.0-cos(i*pi/(k+1)));//图基窗
break;
}
case 3:
{w=1.0-fabs(1.0-2*i/(n-1.0));//三角窗
break;
}
case 4:
{w=0.5*(1.0-cos(2*i*pi/(n-1)));//汉宁窗
break;
}
case 5:
{w=0.54-0.46*cos(2*i*pi/(n-1));//海明窗
break;
}
case 6:
{w=0.42-0.5*cos(2*i*pi/(n-1))+0.08*cos(4*i*pi/(n-1));//布莱克曼窗
break;
}
case 7:
{w=kaiser(i,n,beta);//凯塞窗
break;
}
}
return(w);
}
double CFIRWIN:: kaiser(int i,int n,double beta)
{
double a,w,a2,b1,b2,beta1;
b1=bessel0(beta);
a=2.0*i/(double)(n-1)-1.0;
a2=a*a;
beta1=beta*sqrt(1.0-a2);
b2=bessel0(beta1);
w=b2/b1;
return(w);
}
double CFIRWIN::bessel0(double x)
{
int i;
double d,y,d2,sum;
y=x/2.0;
d=1.0;
sum=1.0;
for(i=1;i<=25;i++)
{d=d*y/i;
d2=d*d;
sum=sum+d2;
if(d2<sum*(1.0e-8)) break;
}
return(sum);
}利用firwin这个函数,我们就可以得到hd(n)了。接下来的工作就是对输入数据序列进行滤波了,由第一部分的公式可以知道,此时有两种做法。
1.直接按照卷积公式进行计算
2.利用FFT先将x(n)和hd(n)变换到频域上,得到X(K)和H(k)后相乘得到Y(K),再进行IFFT即可得到y(n)
下面给出具体代码:
void CWaveProcess::Filter(float *pfSignal,DWORD dwLenSignal,double *h,int N)
{
//法1,直接计算卷积
double *Input_Buffer;
double Output_Data = 0;
Input_Buffer = (double *) malloc(sizeof(double)*N);
memset(Input_Buffer,
0,
sizeof(double)*N);
int Count = 0;
while(1)
{
if(Count==dwLenSignal) break;
Save_Input_Date (pfSignal[Count],
N,
Input_Buffer);
Output_Data = Real_Time_FIR_Filter(h,
N,
Input_Buffer);
pfSignal[Count]=Output_Data;
Count++;
}
//法2,傅里叶变换相乘后,做反傅里叶变换
/* int nPower=(int)(log(N)/log(2))+1;
int nLen=1<<nPower;
Complex *A=new Complex[nLen];
Complex *B=new Complex[nLen];
Complex *C=new Complex[nLen];
int nBlock = (dwLenSignal+nLen-1)/nLen;
CFFT *pA=new CFFT;
CFFT *pB=new CFFT;
CFFT *pC=new CFFT;
for(int i=0; i<nBlock; i++)
{
for(int j=0; j<nLen; j++)
{
if ((DWORD)(i*nLen+j)<dwLenSignal)
{
A[j].real=pfSignal[(DWORD)(i*nLen+j)];
A[j].imag=0.0;
}
else
{
A[j].real=0.0;
A[j].imag=0.0;
}
if (j<N)
{
B[j].real=h[j];
B[j].imag=0.0;
}
else
{
B[j].real=0.0;
B[j].imag=0.0;
}
}
pA->MYFFT(A,nLen);
pB->MYFFT(B,nLen);
for(int _i=0;_i<nLen;_i++)
{
C[_i]=A[_i]*B[_i];//在频域进行乘积
}
pC->MYFFT(C,nLen,true);//然后再在频域反变换回时域,就是卷积
for(j=0;j<nLen;j++)
{
if ((DWORD)(i*nLen+j)<dwLenSignal)
pfSignal[(DWORD)(i*nLen+j)]=C[j].real;
else break;
}
}
delete pA;
delete pB;
delete pC;*/
}
double CWaveProcess::Real_Time_FIR_Filter(double *b,
int b_Lenth,
double *Input_Data)
{
int Count;
double Output_Data = 0;
Input_Data += b_Lenth - 1;
for(Count = 0; Count < b_Lenth ;Count++)
{
Output_Data += (*(b + Count)) *
(*(Input_Data - Count));
}
return (double)Output_Data;
}
void CWaveProcess::Save_Input_Date (double Scand,
int Depth,
double *Input_Data)
{
int Count;
for(Count = 0 ; Count < Depth-1 ; Count++)
{
*(Input_Data + Count) = *(Input_Data + Count + 1);
}
*(Input_Data + Depth-1) = Scand;
}
实际对比两种方法,发现通过fft算法来滤波可提高速度。下面贴出fft算法实现过程,基本思路是,逆序,蝶形计算,利用三重循环控制实现。
void CFFT::MYFFT(Complex *A, int N, bool ifft)//当给ifft赋真值的话进行反变换
{
Complex T;
int m=(int)(log(N)/log(2)),k,P,B,j=N/2,L,i;//m是级数,为2为底N的对数
for(i=1;i<=N-2;i++)//倒序实现,因为经过m次偶奇抽选之后,先前顺序被打乱了,但是打乱后的顺序是有规律的
{
if(i<j)
{
T=A[i];
A[i]=A[j];
A[j]=T;
}
k=N/2;
while(j>=k)
{
j-=k;
k=k/2;
}
j+=k;
}
for(L=1;L<=m;L++)//FFT实现(核心算法时域抽取法)
{
B=1<<(L-1);//这是2的L-1次方
for(j=0;j<=B-1;j++)
{
P=(1<<(m-L))*j;
if(ifft==false)//默认算法为傅里叶正变换
{
for(k=j;k<=N-1;k+=1<<L)
{
T=A[k]+A[k+B]*Complex(cos(-2*PI*P/N),sin(-2*PI*P/N));
A[k+B]=A[k]-A[k+B]*Complex(cos(-2*PI*P/N),sin(-2*PI*P/N));
A[k]=T;
}
}
else//ifft为真的话进行傅里叶反变换
{
for(k=j;k<=N-1;k+=1<<L)
{
T=A[k]+A[k+B]*Complex(cos(-2*PI*P/N),sin(2*PI*P/N));//反变换得取共轭
A[k+B]=A[k]-A[k+B]*Complex(cos(-2*PI*P/N),sin(2*PI*P/N));
A[k]=T;
}
}
}
}
if(ifft==true)//反变换还得除以N
{
for(k=0;k<N;k++)
A[k]=A[k]/N;
}
}
3.结束语
进行数字信号处理可利用的工具有很多,比如matlab,LabVIEW等,这些工具都很强大,使用起来也特别方便。通常C语言要用大量代码实现的过程,matlab一句代码,LabVIEW一个图形就可以代替,因为已经做好了封装,方便使用。但是用C语言的好处就是,能对底层进行修改,使程序设计更加灵活。同时,进行底层语言的编写,可以深入理解原理,加深对数字信号处理这门课程基础知识的掌握。


























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








