题目描述
输入
输出
样例输入
167 198
样例输出
906462341
数据范围
解法
令
f(n)=∑ni=1i
,
g(n)=∑ni=1i2
易得
ans=∑ni=1∑mj=1f(n−i+1)∗f(m−j+1)
等价于
ans=∑ni=1∑mj=1f(i)∗f(j)
显然
f(n)=n∗(n−1)/2
;
拆开得
ans=14∑ni=1∑mj=1i∗(i+1)∗j∗(j+1)
再得
ans=14∑i=1ni∗(i+1)∗∑j=1mj∗(j+1)=14∑i=1n∗(f(i)+g(i))∗∑j=1m∗(f(j)+g(j))
其中 g(n)=16n(n+1)(2n+1)
时间复杂度为 O(log) ,逆元有复杂度。
代码
#include<iostream>
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#define ll long long
#define ln(x,y) ll(log(x)/log(y))
#define sqr(x) ((x)*(x))
using namespace std;
const char* fin="loop.in";
const char* fout="loop.out";
const ll inf=0x7fffffff;
const ll mo=1000000007;
ll n,m,i,j,k,l,tmp,tmd,num,ans;
ll qpower(ll a,ll b){
ll c=1;
while (b){
if (b&1) c=a*c%mo;
a=a*a%mo;
b>>=1;
}
return c;
}
ll N(int a){
return qpower(a,mo-2);
}
ll sum(ll st,ll num){
st%=mo;
num%=mo;
ll en=(st+num-1)%mo;
return (st+en)%mo*num%mo*N(2)%mo;
}
ll xsum(ll n){
n%=mo;
return n*(n+1)%mo*(2*n+1)%mo*N(6)%mo;
}
ll count(ll v){
return (sum(1,v)+xsum(v))%mo;
}
int main(){
freopen(fin,"r",stdin);
freopen(fout,"w",stdout);
scanf("%lld%lld",&n,&m);
ans=count(n)*count(m)%mo*N(4)%mo;
printf("%lld",ans);
return 0;
}启发
∑ 的运算性质
1.
∑(a+b)=∑a+∑b
2.
∑a∑ba∗b=∑aa∗∑bb
3.
∑ik∗f(i)=k∗∑f(i)
∑ni=1i2 公式
∑ni=1i2=16n(n+1)(2n+1)
证明:
利用数学归纳法检验。
设
g(n)=∑ni=1i2
;
先有
g(1)=16∗1∗2∗3=1=∑i=1ni2
如果 g(x) 满足 g(x)=16x(x+1)(2x+1) ;
则
g(x+1)=16x(x+1)(2x+1)+(x+1)2=16(x+1)(6x+6+x(2x+1))=16(x+1)(2x2+7x+6)=16(x+1)(x+2)(2x+3)=16(x+1)[(x+1)+1][2(x+1)+1]
综上得证。











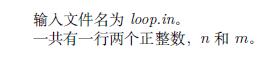
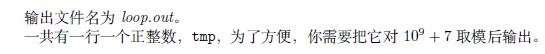


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








