数据结构---二叉树（3）

1.二叉树中和为某一值的路径（剑指offer-25）

题目：输入一颗二叉树和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

解析：这道题考查对二叉树遍历方式的理解，采用先序遍历，如果把二叉树看成图，就是图的深度遍历。使用变量存放当前遍历的路径和，当访问到某一结点时，把该结点添加到路径上，并累加当前结点的值。

如果当前结点为叶结点并且当前路径的和刚好等于输入的整数，则当前的路径符合要求，我们把它打印出来。

如果当前结点不是叶结点，则继续访问它的子结点。

当前结点访问结束后，递归函数将自动回到父结点，因此我们在函数退出之前要在路径上删除当前结点并减去当前结点的值，以确保返回父结点时路径刚好是根结点到父结点的路径。

	// 二叉树中和为某一值的路径
	// pTreeNode--当前根结点
	// expectedSum--期望路径和
	// path--存放路径栈
	// currentSum--当前路径和
	public static void FindPath(Node pTreeNode, int expectedSum, StackX path,
			int currentSum) {

		if (pTreeNode == null)
			return;

		currentSum += pTreeNode.value;
		path.push(pTreeNode.value);

		//当前结点为叶子结点并且路径和满足要求则打印路径
		boolean isLeaf = (pTreeNode.leftChild == null && pTreeNode.rightChild == null);
		if (currentSum == expectedSum && isLeaf) {
			path.printStack();
		}

		//如果不是叶节点，则遍历它的子结点
		if (pTreeNode.leftChild != null)
			FindPath(pTreeNode.leftChild, expectedSum, path, currentSum);
		if (pTreeNode.rightChild != null)
			FindPath(pTreeNode.rightChild, expectedSum, path, currentSum);

		//返回父节点之前，在路径上删除当前结点，并在currentSum中减去当前结点值
		currentSum -= pTreeNode.value;
		path.pop();

	}

注：其中StackX是自己用数组实现的栈，有打印功能。

2.二叉搜索树转换为有序双向链表（剑指offer-27）

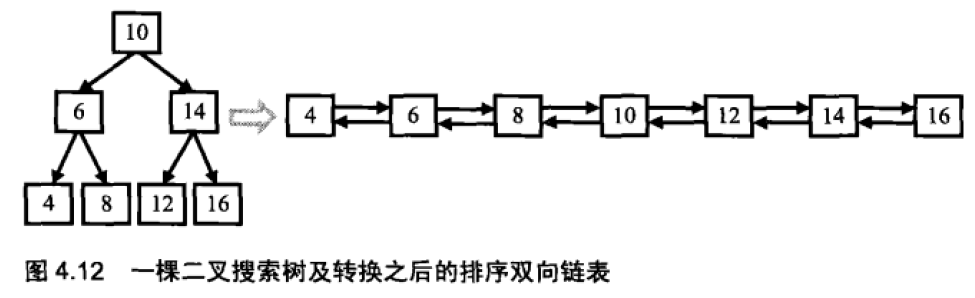
题目：输入一棵二叉搜索树，现在要将该二叉搜索树转换成一个排序的双向链表。而且在转换的过程中，不能创建任何新的结点，只能调整树中的结点指针的指向来实现。

解析：
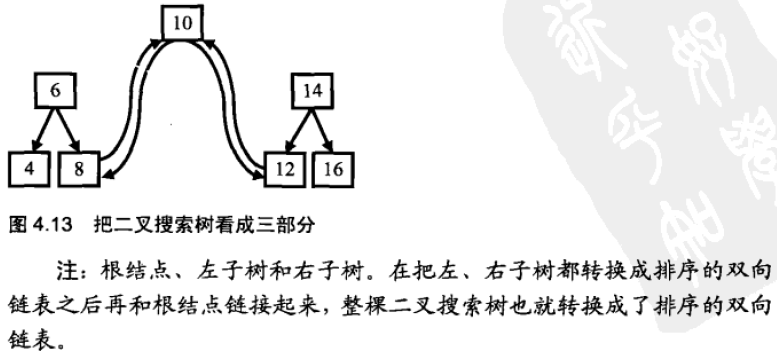
1：由于要求链表是有序的，可以借助二叉树中序遍历，因为中序遍历算法的特点就是从小到大访问结点。当遍历访问到根结点时，假设根结点的左侧已经处理好，只需将根结点与上次访问的最近结点（左子树中最大值结点）的指针连接好即可。进而更新当前链表的最后一个结点指针。
2：由于中序遍历过程正好是转换成链表的过程，即可采用递归处理

	// 递归遍历中的转换过程
	// pNode--处理当前结点
	// pLastNodeInList--当前链表的最后一个结点(初始值为空)
	public static void ConvertNode(Node pNode, Node pLastNodeInList) {
		if (pNode == null)
			return;
		Node pCurrent = pNode;
		
		// 递归处理左子树
		if (pCurrent.leftChild != null)
			ConvertNode(pNode.leftChild, pLastNodeInList);
		
		// 处理当前结点
		pCurrent.leftChild = pLastNodeInList; // 将当前结点的左指针指向已经转换好的链表的最后一个位置
		if (pLastNodeInList != null)
			pLastNodeInList.rightChild = pCurrent;// 将已转换好的链表的最后一个结点的右指针指向当前结点
		pLastNodeInList = pCurrent;// 更新链表的最后一个结点
				
		// 递归处理当前结点的右子树
		if (pCurrent.rightChild != null)
			ConvertNode(pNode.rightChild, pLastNodeInList);
	}

	public static Node Convert(Node pRootInTree) {
		
		Node pLastNodeInList = null;
		ConvertNode(pRootInTree, pLastNodeInList);

		// pLastNodeInList指向双向链表的尾结点，再次遍历找到头结点
		Node pHeadOfList = pLastNodeInList;
		while (pHeadOfList != null && pHeadOfList.leftChild != null)
			pHeadOfList = pHeadOfList.leftChild;

		return pHeadOfList;
	}