各种优化方法总结比较（sgd/momentum/Nesterov/adagrad/adadelta）

最新推荐文章于 2024-06-01 23:15:00 发布
最新推荐文章于 2024-06-01 23:15:00 发布
阅读量584 收藏 2
点赞数
分类专栏： 机器学习 文章标签： 深度学习

前言

这里讨论的优化问题指的是，给定目标函数f(x)，我们需要找到一组参数x，使得f(x)的值最小。

本文以下内容假设读者已经了解机器学习基本知识，和梯度下降的原理。

SGD

SGD指stochastic gradient descent，即随机梯度下降。是梯度下降的batch版本。

对于训练数据集，我们首先将其分成n个batch，每个batch包含m个样本。我们每次更新都利用一个batch的数据，而非整个训练集。即： 

xt+1=xt+Δxt

Δxt=−ηgt

其中， η 为学习率， gt 为x在t时刻的梯度。

这么做的好处在于：

  • 当训练数据太多时，利用整个数据集更新往往时间上不显示。batch的方法可以减少机器的压力，并且可以更快地收敛。
  • 当训练集有很多冗余时（类似的样本出现多次），batch方法收敛更快。以一个极端情况为例，若训练集前一半和后一半梯度相同。那么如果前一半作为一个batch，后一半作为另一个batch，那么在一次遍历训练集时，batch的方法向最优解前进两个step，而整体的方法只前进一个step。

Momentum

SGD方法的一个缺点是，其更新方向完全依赖于当前的batch，因而其更新十分不稳定。解决这一问题的一个简单的做法便是引入momentum。

momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力： 

Δxt=ρΔxt−1−ηgt

其中， ρ  即momentum，表示要在多大程度上保留原来的更新方向，这个值在0-1之间，在训练开始时，由于梯度可能会很大，所以初始值一般选为0.5；当梯度不那么大时，改为0.9。 η  是学习率，即当前batch的梯度多大程度上影响最终更新方向，跟普通的SGD含义相同。 ρ  与  η  之和不一定为1。

Nesterov Momentum

这是对传统momentum方法的一项改进，由Ilya Sutskever(2012 unpublished)在Nesterov工作的启发下提出的。

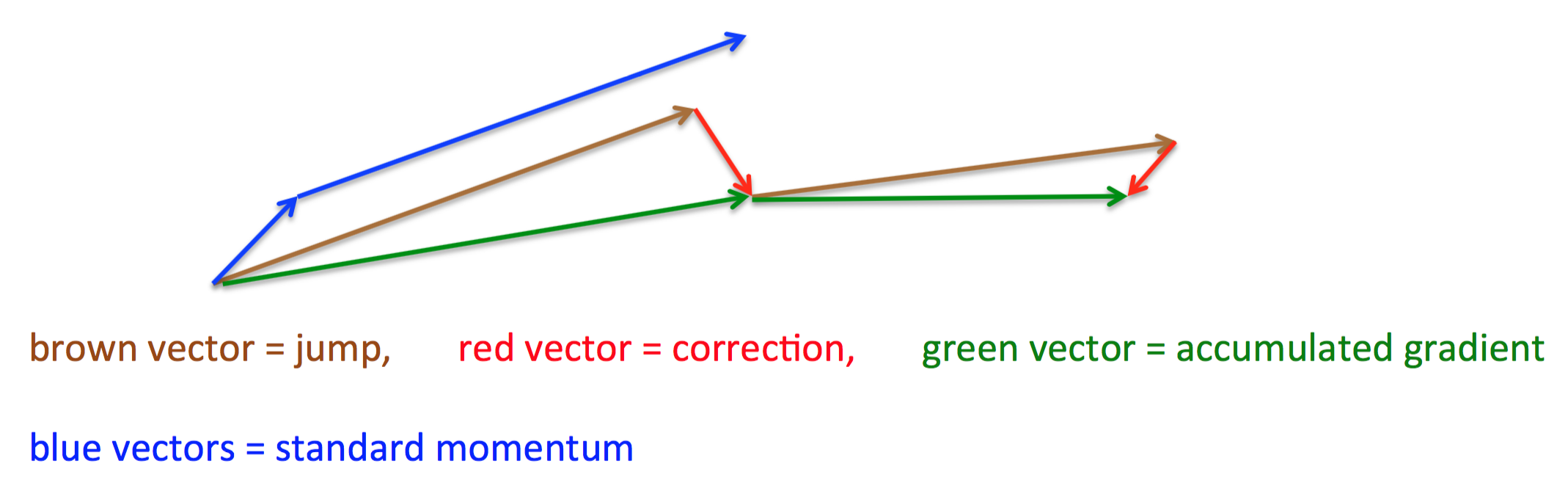
其基本思路如下图（转自Hinton的coursera公开课lecture 6a）：

Nesterov Momentum

首先，按照原来的更新方向更新一步（棕色线），然后在该位置计算梯度值（红色线），然后用这个梯度值修正最终的更新方向（绿色线）。上图中描述了两步的更新示意图，其中蓝色线是标准momentum更新路径。

公式描述为： 

Δxt=ρΔxt−1−ηΔf(xt+ρΔxt−1)

Adagrad

上面提到的方法对于所有参数都使用了同一个更新速率。但是同一个更新速率不一定适合所有参数。比如有的参数可能已经到了仅需要微调的阶段，但又有些参数由于对应样本少等原因，还需要较大幅度的调动。

Adagrad就是针对这一问题提出的，自适应地为各个参数分配不同学习率的算法。其公式如下： 

Δxt=−η∑tτ=1g2τ+ϵ‾‾‾‾‾‾‾‾‾‾‾√gt

其中 gt  同样是当前的梯度，连加和开根号都是元素级别的运算。 eta  是初始学习率，由于之后会自动调整学习率，所以初始值就不像之前的算法那样重要了。而 ϵ 是一个比较小的数，用来保证分母非0。

其含义是，对于每个参数，随着其更新的总距离增多，其学习速率也随之变慢。

Adadelta

Adagrad算法存在三个问题

  • 其学习率是单调递减的，训练后期学习率非常小
  • 其需要手工设置一个全局的初始学习率
  • 更新 xt 时，左右两边的单位不同一

Adadelta针对上述三个问题提出了比较漂亮的解决方案。

首先，针对第一个问题，我们可以只使用adagrad的分母中的累计项离当前时间点比较近的项，如下式： 

E[g2]t=ρE[g2]t−1+(1−ρ)g2t

Δxt=−ηE[g2]t+ϵ‾‾‾‾‾‾‾‾‾√gt

这里 ρ 是衰减系数，通过这个衰减系数，我们令每一个时刻的 gt 随之时间按照 ρ 指数衰减，这样就相当于我们仅使用离当前时刻比较近的 gt 信息，从而使得还很长时间之后，参数仍然可以得到更新。

针对第三个问题，其实sgd跟momentum系列的方法也有单位不统一的问题。sgd、momentum系列方法中： 

Δx的单位∝g的单位∝∂f∂x∝1x的单位

类似的，adagrad中，用于更新 Δx 的单位也不是x的单位，而是1。

而对于牛顿迭代法： 

Δx=H−1tgt

其中H为Hessian矩阵，由于其计算量巨大，因而实际中不常使用。其单位为： 
Δx∝H−1g∝∂f∂x∂2f∂2x∝x的单位

注意，这里f无单位。因而，牛顿迭代法的单位是正确的。

所以，我们可以模拟牛顿迭代法来得到正确的单位。注意到： 

Δx=∂f∂x∂2f∂2x⇒1∂2f∂2x=Δx∂f∂x

这里，在解决学习率单调递减的问题的方案中，分母已经是 ∂f∂x 的一个近似了。这里我们可以构造 Δx 的近似，来模拟得到 H−1 的近似，从而得到近似的牛顿迭代法。具体做法如下： 
Δxt=−E[Δx2]t−1‾‾‾‾‾‾‾‾‾‾√E[g2]t+ϵ‾‾‾‾‾‾‾‾‾√gt

可以看到，如此一来adagrad中分子部分需要人工设置的初始学习率也消失了，从而顺带解决了上述的第二个问题。

各个方法的比较

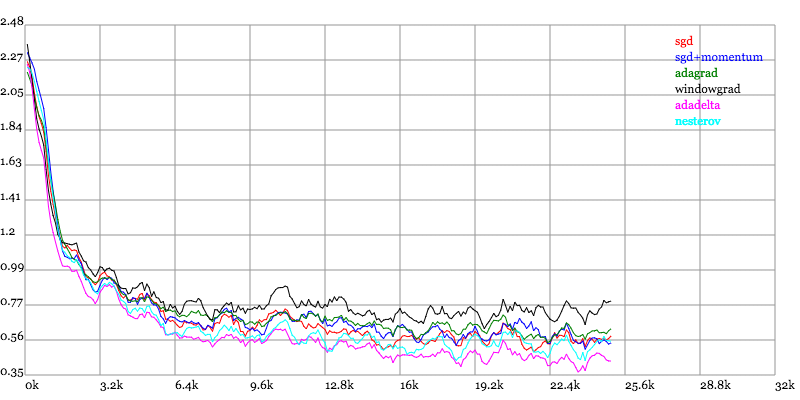
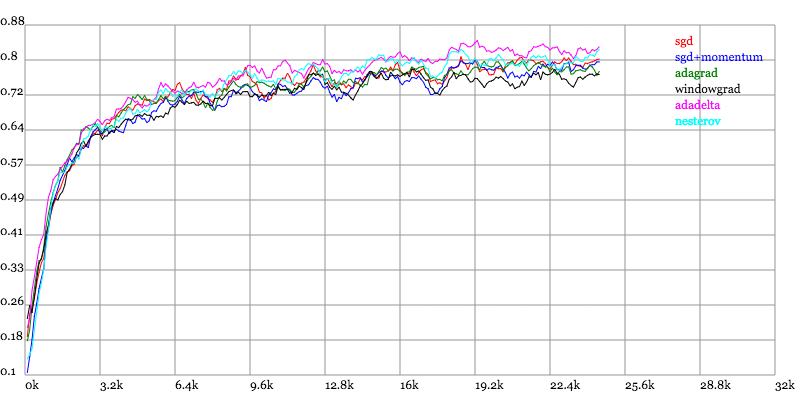
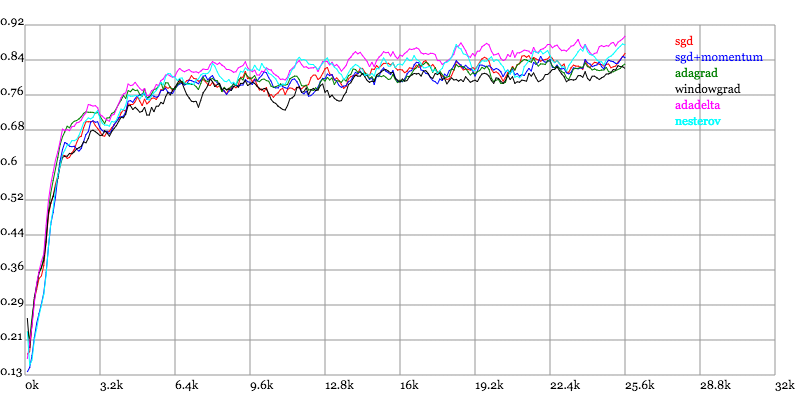
Karpathy做了一个这几个方法在MNIST上性能的比较，其结论是： 
adagrad相比于sgd和momentum更加稳定，即不需要怎么调参。而精调的sgd和momentum系列方法无论是收敛速度还是precision都比adagrad要好一些。在精调参数下，一般Nesterov优于momentum优于sgd。而adagrad一方面不用怎么调参，另一方面其性能稳定优于其他方法。

实验结果图如下：

Loss vs. Number of examples seen 
Loss vs. Number of examples seen

Testing Accuracy vs. Number of examples seen 
Testing Accuracy vs. Number of examples seen

Training Accuracy vs. Number of examples seen这里写图片描述

其他总结文章

最近看到了一个很棒的总结文章，除了本文的几个算法，还总结了RMSProp跟ADAM（其中ADAM是目前最好的优化算法，不知道用什么的话用它就对了）

参考：

http://blog.csdn.net/luo123n/article/details/48239963

https://www.cnblogs.com/neopenx/p/4768388.html

https://github.com/tsycnh/mlbasic

https://zhuanlan.zhihu.com/p/22252270

hlang8160
关注
专栏目录
若干新型智能优化算法对比分析研究
罗伯特技术屋
12-14 3010
智能优化算法（IOA）指的是一类以自然界的生物生存进化过程或物理现象为算法原理,用于解决最优化问题的算法,较为知名的智能优化算法有遗传算法、粒子群算法、模拟退火算法等。选取了近几年国内外提出的几种新型智能优化算法：蝴蝶优化算法（BOA）、飞蛾扑火算法（MFO）、正弦余弦优化算法（SCA）、蝗虫优化算法（GOA）、哈里斯鹰优化算法（HHO）、麻雀搜索算法（SSA）。仿植物生长类算法指的是模拟花草树木等植物在生长过程中表现出来的向光性、根的吸水性、种子繁殖、花朵授粉等特性而构造出的优化算法。
优化方法总结比较(SGD,Momentum,Nesterov,Adagrad,Adadelta,RMSprop,Adam,Adamax,Nadam,DFP,BFGS)
瑾瑜将将的专栏
04-08 791
随机梯度下降法 Batch Gradient Descent 在每一轮的训练过程中，BGD算法用整个训练集的数据计算loss的梯度，并用该梯度对模型参数进行更新： θt+1=θt+Δθ,Δθ=−η∗gt\theta_{t+1}=\theta_{t}+\Delta\theta, \Delta\theta=-\eta * g_{t}θt+1​=θt​+Δθ,Δθ=−η∗gt​ 优点 loss若为凸函...
各种最优化方法比较
SCAU_Jimmy的专栏
02-21 4433
梯度下降法： 用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，所以也被称为是”最速下降法“。最速下降法越接近 目标值，步长越小，前进越慢。    批量梯度下降法： 最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小，但是对于大规模样本问题效率低下。    随机梯度下降法： 最小化每条样本的损
常见的几种最优化方法
wsyhawl的博客
10-12 449
http://www.cnblogs.com/maybe2030/p/4751804.html
不同智能优化算法如何进行性能分析比较？
Tsingke
06-29 5302
不同智能优化算法如何进行性能分析比较？ 智能优化算法一类随机优化算法，算法每次执行结果略有差异， 该类算法通常通过模仿现实生活中的某种行为机制的方式而被提出，不同种类的算法优化机理不同，即使同一算法及其改进算法在搜索机理上也往往存在很大差别。对于搜索性能稳定的算法这种差异相对较小，而对于搜索性能波动较大的算法每次执行结果差异较为明显。如何衡量算法间的优劣呢？为此，学术界提出了多种...
深度学习优化器的原理总结（SGD/SGD with momentum/Adagrad/AdaDelta/RMSProp/Adam/Nadam）
cyy2learn的博客
04-24 3537
优化器的框架： 目标函数关于当前参数的梯度 ; 根据历史梯度计算一阶动量与二阶动量： ; ; 计算当前时刻的下降梯度： ​​​​​​​; 根据更新参数： ​​​​​​​; 现在我们来一个个分析现有的优化器，如何套入以上的框架。 简单来说，它们的区别就在于和的定义。 SGD 特点：没有使用动量...
深度学习最优化（四）—— 动量法/Nesterov/Adagrad/Adadelta/RMSprop/Adam/Nadam
manmanxiaowugun的博客
10-16 4920
1. SGD 现在的SGD一般都指小批量梯度下降，即每一次迭代计算mini-batch的梯度，然后对参数进行更新。 其中是模型参数，是模型目标函数，是目标函数的梯度，是学习率。 难点（缺点）： （1）学习率的选择。过低收敛缓慢，过高无法收敛。 （2）“...
斯坦福cs231n学习笔记（11）------神经网络训练细节（梯度下降算法大总结/SGD/Momentum/AdaGrad/RMSProp/Adam/牛顿法）
huplion的专栏
01-28 2万+
神经网络训练细节系列笔记： 神经网络训练细节（激活函数） 神经网络训练细节（数据预处理、权重初始化） 神经网络训练细节（Batch Normalization） 神经网络训练细节（训练过程，超参数优化） 通过学习，我们知道，因为训练神经网络有个过程: Sample 获得一批数据； Forward 通过计算图前向传播，获得loss； Backprop 反向传播计算梯度，这个梯度能告诉我
深度学习优化算法对比：SGD、Momentum、Nesterov、Adagrad等
"这篇文章除了探讨SGD（Mini-Batch Gradient Descent）的基本概念和缺点外，还介绍了优化算法Momentum、Nesterov Accelerated Gradient (NAG)的原理，以及它们如何改善SGD的性能。接着，文章提到了自适应学习率的...
优化算法比较
qq_46644680的博客
04-16 556
本文介绍了常用的优化算法
灰狼优化算法和粒子群优化算法比较
09-12
本资源包含灰狼优化算法（GWO）代码以及粒子群算法（PSO），主函数为使用灰狼优化和粒子群优化对不同函数进行寻优并将两种算法的比较结果绘图显示
优化方法Sgd，Nesterov，Adagrad，Adadelta，RMSprop，Adam推导理解
想要游向大海的鱼
06-17 317
目标检测经典论文——YOLOv4论文翻译：YOLOv4: Optimal Speed and Accuracy of Object Detection（YOLOv4: 目标检测最优速度和精度）
bigcindy的博客
08-01 7270
YOLOv4: Optimal Speed and Accuracy of Object Detection YOLOv4: 目标检测最优速度和精度 Alexey Bochkovskiy* alexeyab84@gmail.com Chien-Yao Wang* Institute of Information Science Academia Sinica, Taiwan kinyiu@iis.sinica.edu....
深度学习优化算法比较
最新发布
weixin_42132035的博客
06-01 1041
RMSprop（Root Mean Square Propagation）是一种用于训练神经网络的自适应学习率方法，旨在解决Adagrad方法在训练深层网络时学习率逐渐减小到无法进行有效学习的问题。RMSprop通过引入衰减系数，使得历史梯度的累积效应被限制，从而保持了一定的学习速率，这使得它成为深度学习中非常流行且有效的优化算法之一。选择合适的优化算法可以显著影响深度学习模型的性能和训练速度。虽然没有一种算法在所有情况下都是最优的，但理解它们的原理、优缺点和适用场景可以帮助研究者和开发者做出明智的选择。
【2023年算法比较】13种最新智能优化算法大比拼（Matlab代码实现）
weixin_61181717的博客
02-19 2041
if ~strcmp(number,'F16')&&~strcmp(number,'F9')&&~strcmp(number,'F11') %这里是因为这几个函数收敛太快，不适用于semilogy，直接plot。8. CDO（Colliding Bodies Optimization）：基于物体碰撞行为的优化算法，模拟物体之间的碰撞和反弹来搜索最优解。3. WOA（Whale Optimization Algorithm）：基于鲸鱼社会行为的优化算法，模拟鲸鱼的追逐和协作行为来搜索最优解。
全局优化算法：遗传算法
Sonnet
02-26 2万+
全局优化算法概述前面讨论过一些迭代算法，包括牛顿法、梯度方法、共轭梯度方法和拟牛顿法，能够从初始点出发，产生一个迭代序列。很多时候，迭代序列只能收敛到局部极小点。因此，为了保证算法收敛到全局最小点，有时需要在全局极小点附近选择初始点。此外，这些方法需要计算目标函数。全局优化算法又称现代启发式算法，是一种具有全局优化性能、通用性强且适合于并行处理的算法。 这种算法一般具有严密的理论依据，而不是单纯凭
keras的主要模块介绍
热门推荐
Ezrealmore
10-19 2万+
keras是一个开源是的python深度学习库，可以基于theano或者tenserflow，下面大体介绍下keras的使用方法一、几个重要的模块1、优化器（optimizers）优化器是调整每个节点权重的方法，看一个代码示例：model = Sequential() model.add(Dense(64, init='uniform', input_dim=10)) model.add(Acti
PyTorch优化算法：torch.optim.SGD的参数详解和应用
weixin_51659315的博客
01-19 1万+
torch.optim.SGD 是 PyTorch 中用于实现随机梯度下降（Stochastic Gradient Descent，SGD）优化算法的类。示例中，创建了一个线性模型，使用均方误差损失，并使用 torch.optim.SGD 作为优化器。它是一个正数，控制每次参数更新的步长。（默认值为 0）: 动量（momentum）是一个用于加速 SGD 收敛的参数。（默认值为 0）: 阻尼项，用于减缓动量的速度。（必须参数）: 这是一个包含了需要优化的参数（张量）的迭代器，例如模型的参数。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值