计算机体系结构----指令流水线吞吐率、效率计算

每段时间相同

一条指令流水线被分为k段，每一段时间都为$\Delta t$，连续输入n条指令。

处理完n个任务所用的时间记作$T_k$：
$$T_k=k\Delta t+(n-1)\Delta t$$
这个比较好理解，看时空图即可

吞吐率记作$TP$：
$$TP=\frac{n}{T_k}=\frac{n}{k\Delta t+(n-1)\Delta t}$$
n个任务，用n除以总时间，就是每个任务的平均处理时间，平均多久处理一个任务，就是吞吐率。

效率：流水线中的设备实际使用时间与整个运行时间的比值，即流水线设备的利用率。

一共分为k段，需要k个设备，那么每个设备的效率我们记作$e_i$

一个设备，在整个过程中，每一条指令都要使用一次，所以使用了n次，加上每一次都是$\Delta t$，所以就是$n\Delta t$
$$e_i=\frac{n\Delta t}{T_k}=\frac{n\Delta t}{k\Delta t+(n-1)\Delta t}=\frac{n}{k+n-1}$$
（ps：注意，这个只符合，当一个设备每一条指令都会使用它的情况。飞此情况的，并不适用。其实还是从定义出发，效率就是所有设备的实际运行时间，与整个运行时间的比值，其实就是时空图里面被填满的格子，比上总的面积。）
那么整段流水线的效率呢，就是每一段的效率，加起来，求个平均值。

又因为这每一段的效率都一样，所以求均值和不求一样。故整段流水线的效率为：
$$E=\frac{e_1+e_2+...+e_k}{k}=\frac{k{e}_1}{k}=e_1=\frac{n\Delta t}{T_k}=\frac{n}{k+n-1}$$
这个结果其实还可以写作：
$$E=\frac{n\Delta t}{T_k}=TP\Delta t$$

每段时间不同

一条指令流水线被分为k段，k段时间分别为$e_1,e_2,...,e_k$，连续输入n条指令。

处理完n个任务所用的时间记作$T_k$：
$$T_k=\sum _{i=1}^k\Delta t_i+(n-1)max(\Delta t_1,\Delta t_2,...,\Delta t_k)$$
为什么是这样呢，看图。这个也好理解，直接看最长的那一段，从头到尾，最长的那一段一共执行了n次，那再观察时空图的末尾，最长的那一段过后，还执行了两小段，再观察时空图的开头，最长的那一段执行之前，还执行了一小段，这前后两部分，其实就是一个指令完整的执行流程，但不包括最长的那一段。所以啊，从n次执行中拿出来一个最长的，跟他们合在一起，就是一次完整的指令执行过程，所以最终的公式就是：一次完整的执行过程+（n-1）次最长的执行过程。

吞吐率$TP$：
$$TP=\frac{n}{{\sum }_{i=1}^k\Delta t_i+(n-1)max(\Delta t_1,\Delta t_2,...,\Delta t_k)}$$
效率：

先说一小段的效率$e_i$
$$e_i=\frac{n\Delta t_i}{T_k}=\frac{n\Delta t_i}{{\sum }_{i=1}^k\Delta t_i+(n-1)max(\Delta t_1,\Delta t_2,...,\Delta t_k)}$$
那总的效率E就是每一段的加起来，求均值

先看每一段加起来
$$e_1+e_2+...+e_k=\frac{n\Delta t_1}{T_k}+\frac{n\Delta t_2}{T_k}+...=\frac{n{\sum }_{i=1}^k\Delta t_i}{T_k}$$
再求均值，那就是除以k
$$E=\frac{n{\sum }_{i=1}^k\Delta t_i}{k{T}_k}=\frac{n{\sum }_{i=1}^k\Delta t_i}{k{\sum }_{i=1}^k\Delta t_i+(n-1)max(\Delta t_1,\Delta t_2,...,\Delta t_k)}$$
这个结果，里面那一部分其实就是TP，所以，还可以写为
$$E=TP\frac{1}{k}\sum _{i=1}^k\Delta t_i$$
瓶颈问题：

我们把流水线中这种时间最长的段称为流 水线的瓶颈段。如图，$S_2$就是瓶颈段。

解决瓶颈段有两个方法：

• 细分瓶颈段

• 

• 重复设置瓶颈段

• 

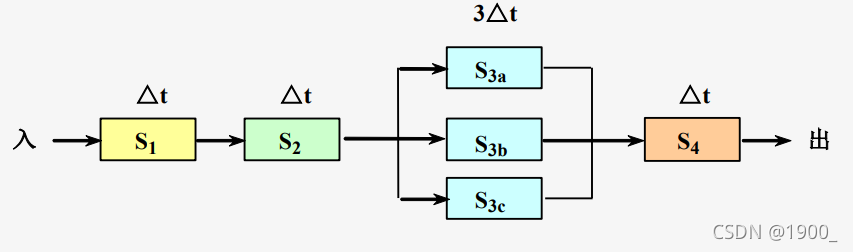
重复设置瓶颈段后的时空图：
9条指令

重复设置瓶颈段的缺点是：控制逻辑比较复杂，所需的硬件增加了。

加速比

加速比：完成同样一批任务，不使用流水线所用的时间与使用流水线所用
的时间之比。
使用流水线的时间是$TP$
不用流水线的时间，就是每一条指令所需时间加起来。