K-means 计算 anchor boxes

k-means原理

K-means算法是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

问题

K-Means算法主要解决的问题如下图所示。我们可以看到，在图的左边有一些点，我们用肉眼可以看出来有四个点群，K-Means算法被用来找出这几个点群。

算法概要

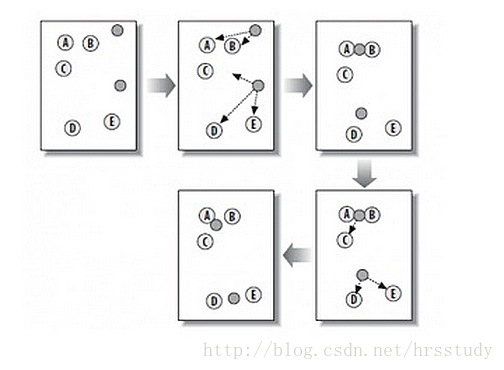
从上图中，我们可以看到，A, B, C, D, E 是五个在图中点。而灰色的点是我们的种子点，也就是我们用来找点群的点。有两个种子点，所以K=2。

然后，K-Means的算法如下：

随机在图中取K（这里K=2）个种子点。
然后对图中的所有点求到这K个种子点的距离，假如点Pi离种子点Si最近，那么Pi属于Si点群。（上图中，我们可以看到A,B属于上面的种子点，C,D,E属于下面中部的种子点）
接下来，我们要移动种子点到属于他的“点群”的中心。（见图上的第三步）
然后重复第2）和第3）步，直到，种子点没有移动（我们可以看到图中的第四步上面的种子点聚合了A,B,C，下面的种子点聚合了D，E）。

k-means算法缺点

1、需要提前指定k
2、k-means算法对种子点的初始化非常敏感

k-means++算法

k-means++是选择初始种子点的一种算法，其基本思想是：初始的聚类中心之间的相互距离要尽可能的远。

方法如下：
1.从输入的数据点集合中随机选择一个点作为第一个聚类中心
2.对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)
3.选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大
4.重复2和3直到k个聚类中心被选出来
5.利用这k个初始的聚类中心来运行标准的k-means算法

第2、3步选择新点的方法如下：
a.对于每个点，我们都计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里，然后把这些距离加起来得到Sum(D(x))。
b.然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先用Sum(D(x))乘以随机值Random得到值r，然后用currSum += D(x)，直到其currSum>r，此时的点就是下一个“种子点”。原因见下图：