用大数取模思想解决“又是斐波那契数列”问题

雨花絮语

于 2023-11-21 20:27:06 发布

阅读量208

点赞数 6

文章标签：算法数据结构 c语言学习 c++ 贪心算法

本文链接：https://blog.csdn.net/hua3473489608/article/details/134538800

版权

概念引入

我们在算法题中，有时可能会遇到大数取模的问题，就是当程序运行得出一个结果后，要对其进行取模运算。

大数取模的原因：

第一个，大数越界。一般来说，当程序的测试参数较大时，方法的执行会超过Int 32 甚至是Int 64 的取值范围，最终导致错误的返回值。

第二个，int 32位的取值范围是-2147483648～2147483647，而1000000007是最小的十位数的质数。对结果进行1000000007取模，可以保证值永远在int的范围之内。

第三个，int64位的最大值为2^63-1，对于1000000007来说它的平方不会在int64中溢出。

大数取模的具体过程：

举个例子：4567这个数，我们知道4567%5=2，那么我们就用大数取模的思想来求这个数的模。

1：在数学中我们可以把4567拆分成(((4*10+5)*10+6)*10+7)

2：下面我们从内向外对每一步对5求余

(4*10+5)%5=0;此时等式为((0*10+6)*10+7)

(0*10+6)%5=1;此时等式为(1*10+7)

(1*10+7)%5=2;此时等式为2

3：从上面我们可以推出4567%5=((((4*10+5)*10%5+6)*10%5+7)%5)

取模公式

有兴趣的同学可以自己证明一下

1.两数相加再取模
(m + n) % p = (m%p + n%p) %p

2.两数相乘再取模
(m * n) % p = (m%p) * (n%p) %p

3.两数相减再取模
(m - n) % p = ((m%p - n%p) + p) %p

问题分析：

看到这里我们已经对大数取模有了更深入的了解，下面就以“又是斐波那契数列”问题为例，来具体分析一下大数取模思想是如何运用的吧！

如题所示：

有另一种斐波那契数列：F0=7，F1=11，Fn=Fn−1+Fn−2(n≥2)。

输入格式

输入数据有多行组成，每一行上是一个整数 n(n≤106)。

输出格式

如果 Fn能被 3整除，那么打印一行"yes"，否则，打印一行"no"。

提示

先使用数组把 1∼10^6的 Fi计算出来，然后每次查询，要不然会超时的。

打表：

题上提示说先把1~10^6的 Fi计算出来，那么我们就可以定义一个数组(表)，来求出范围内所有的Fi

int a[1000005]={7,11};//a[0]=7,a[1]=11
void fibonacci()
{
	for(int i=2;i<=1e6;i++){
		a[i]=(a[i-1]+a[i-2]);
	}
}

主函数：

int main()
{
	int n;
	fibonacci();
	while(~scanf("%d",&n))
	{
		printf("%d\n",a[n]);
	}
	return 0;
}

你发现你测试样例一点都没问题，但是测试样例就过了三个，这是为什么呢？

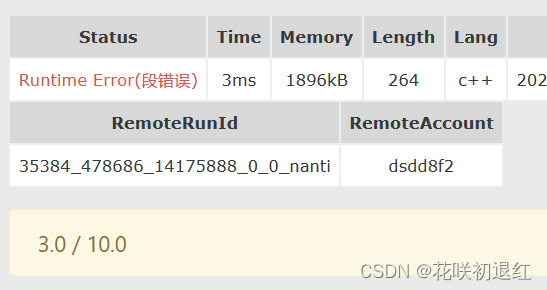
细心读题你就会发现，这题压根就不是让你求Fi，因为最后10^6的Fi太大了，如果 Fn能被 3整除，那么打印一行"yes"，否则，打印一行"no"。其实你最后只需要要Fi%3的值就行了，等于0输出yes否则输出no

对比一下，我是直接存Fi还是存Fi%3，其实一眼就能看懂了吧！

int a[1000005]={7,11};
void fibonacci()
{
	for(int i=2;i<=1e6;i++){
		a[i]=(a[i-1]+a[i-2])%3;//防止数据溢出
	}
}

这样以来我们就把数组数据溢出的问题解决了

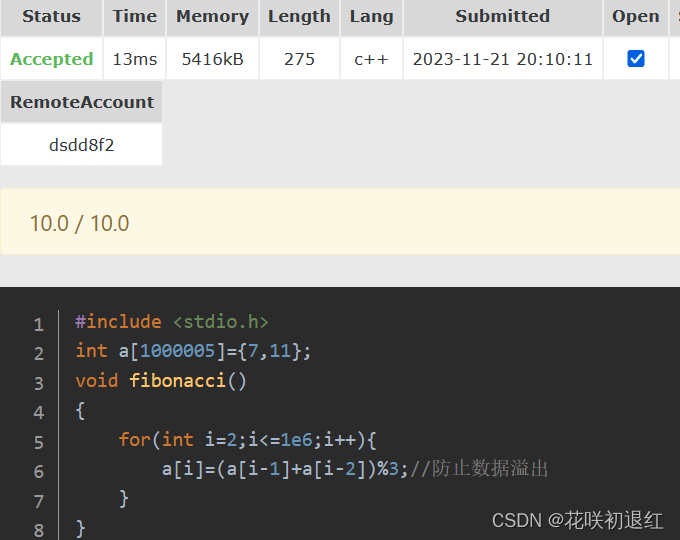
我们由取模公式可得，(m + n) % p = (m%p + n%p) %p

int a[1000005]={7,11};
void fibonacci()
{
	for(int i=2;i<=1e6;i++){
		a[i]=(a[i-1]%3+a[i-2]%3)%3;//防止数据溢出
	}
}

好了到这里“又是斐波那契数列”问题我们已经完美解决了

完整代码如下：

#include <stdio.h>
int a[1000005]={7,11};
void fibonacci()
{
	for(int i=2;i<=1e6;i++){
		a[i]=(a[i-1]%3+a[i-2]%3)%3;//防止数据溢出
	}
}
int main()
{
	int n;
	fibonacci();
	while(~scanf("%d",&n))
	{
		if(a[n]%3==0){
			printf("yes\n");
		}
		else{
			printf("no\n");
		}
	}
	return 0;
}

总结

对于大数取模，我们可以使用以下方法来优化计算：

1. 费马小定理：对于质数p和整数a，a^(p-1) ≡ 1 (mod p)。因此，如果p为质数，则a^b mod p = a^(b mod (p-1)) mod p。

2. 快速幂算法：将指数b表示为二进制形式，例如b = 10101，即b = 1*2^4 + 0*2^3 + 1*2^2 + 0*2^1 + 1*2^0。则a^b = a^(1*2^4) * a^(0*2^3) * a^(1*2^2) * a^(0*2^1) * a^(1*2^0)。这样就可以使用快速幂算法来计算a^b。

3. 模运算的分配律：(a+b) mod p = (a mod p + b mod p) mod p，(a-b) mod p = (a mod p - b mod p) mod p，(a*b) mod p = (a mod p * b mod p) mod p。

4. 防止溢出：在进行乘法时，如果两个数的乘积超出了数据类型的范围，则需要使用高精度计算或者分治法来处理。

5. 模数的选择：当模数为质数时，计算速度会更快，但是当模数太大时，会导致溢出。因此，需要根据实际情况来选择合适的模数。

综上所述，对于大数取模问题，我们可以使用上述方法来优化计算，提高计算效率。