Problem
Description
Input
Output
Sample Input
4 3 5
4 1 7 3
4 7 4 8
Sample Output
59716
Data Constraint
Solution
不要看到
N≤105
就害怕,其实这题很简单的。
对于a=0,答案就是
Tn∗bn−1
.
我们可以发现,只有L数组和T数组控制着答案。每次向右就乘以a,向下就乘以b,所以我们可以得到答案是
Σni=2Cn−i2n−i−2∗(an−1bn−i∗l[i]+an−ibn−1∗t[i])
可是这样还是超时啊!!!!!!!!!!!!
那么我们可以将阶乘、逆元预处理啊……………………
Code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#define N 100010
#define LL long long
#define mo 1000000007
#define fo(i,a,b) for(i=a;i<=b;i++)
using namespace std;
int a,b,i,j,n,m;
LL l[N],t[N],ans,jc[N*2],jj[N*2];
LL ksm(LL x,LL y)
{
LL s=1,t=x;
while (y)
{
if (y%2==1) s=(s*t)%mo;
t=(t*t)%mo;
y/=2;
}
return s;
}
int main()
{
scanf("%d%d%d",&n,&a,&b);
fo(i,1,n) scanf("%lld",&l[i]);
fo(i,1,n) scanf("%lld",&t[i]);
jj[0]=jj[1]=jc[0]=jc[1]=1;
fo(i,2,n*2)
{
jc[i]=(jc[i-1]*i)%mo;
jj[i]=ksm(jc[i],mo-2);
}
ans=0;
fo(i,2,n)
{
LL t1,t2,t3;
t1=(((jc[2*n-i-2]*jj[n-i])%mo)*jj[n-2])%mo;
t2=((ksm(a,n-1)*ksm(b,n-i)%mo)*l[i])%mo;
t3=((ksm(a,n-i)*ksm(b,n-1)%mo)*t[i])%mo;
ans=(ans+t1*((t2+t3)%mo))%mo;
}
printf("%lld",ans);
}——2016.8.17










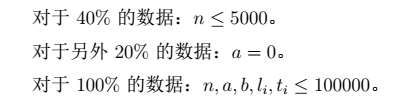

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








