一、点估计
参数的点估计就是根据样本构造一个统计量,作为总体未知参数的估计。这个统计量称为未知参数的估计量。
在统计中,经常使用的点估计量有:
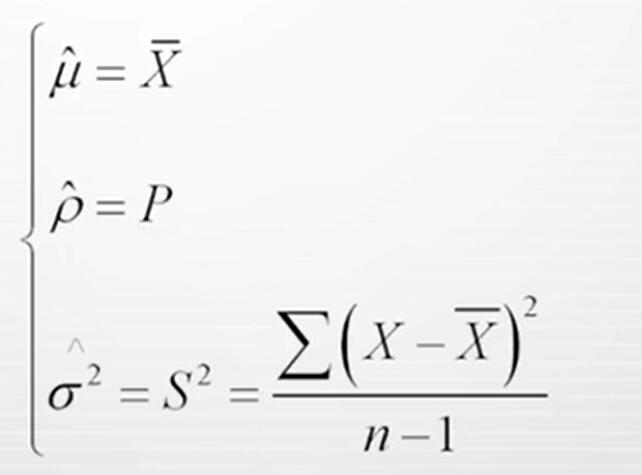
二、估计量的评价标准
1、无偏性
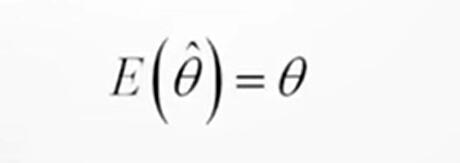
无偏性即指估计量抽样分布的数学期望等于总体参数的真值。
2、有效性
如果两个估计量都是无偏的,那么离散程度较小的估计量相对来说是更有效的。对于离散程度,我通常使用方差来衡量。 比如,简单算术平均数和加权平均数,它们都具有无偏性。但是简单算术平均数的方差比加权平均数小。因此,我们应该选简单算术平均数。
3、一致性
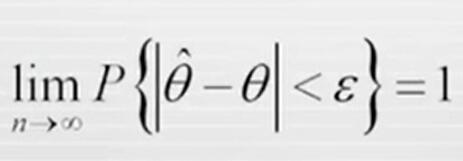
随着样本量的增大,估计量的值本身如果稳定于总体参数的真值,那么这个估计量就有一致性。即:随着样本量的无限增加,样本估计量就充分靠近总体参数,该统计量满足一致性的要求。样本越大估计越准确。
更多内容,请参考《估计量的有效性和一致性》








 本文介绍了参数统计中的点估计概念,即利用样本构造统计量来估计总体未知参数。讨论了估计量的三个重要评价标准:无偏性,意味着估计量的期望值等于参数真实值;有效性,比较无偏估计量的方差以选择离散程度小的;一致性,当样本量增加时,估计量趋向于参数真值。这些标准帮助我们评估和选择更好的估计方法。
本文介绍了参数统计中的点估计概念,即利用样本构造统计量来估计总体未知参数。讨论了估计量的三个重要评价标准:无偏性,意味着估计量的期望值等于参数真实值;有效性,比较无偏估计量的方差以选择离散程度小的;一致性,当样本量增加时,估计量趋向于参数真值。这些标准帮助我们评估和选择更好的估计方法。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








