HIT 系统生物学 基于蛋白互作网络的关键模块发现算法实现及分析 参考代码

目录

实验目的：

实验内容：

实验要求：

实验步骤：

1.从多个站点下载小型蛋白质互通网络

2.计算PPI网络的拓扑特征

3.实施3种以上的网络模块识别算法， 并使用这些算法来识别重要的蛋白质网络模块

4.编写标记为重要的网络可视化程序网络中的功能模块

5.比较基于不同算法的模块，并分析实验结果不同的原因 

聚类运行时间分析：

聚类模块数量分析：

模块度分析：

各社区分析：

交叉分析：

参考代码：

---

实验目的：

深入了解识别蛋白质-蛋白质相互作用网络关键模块的算法，并从网络中查找重要模块。

实验内容：

1.利用现有的蛋白质相互作用网络，使用三种算法确定重要模块，并计算拓扑特征（网络拓扑属性）。

2.使用软件工具显示蛋白质网络的模块。

3.比较不同算法识别的模块。

实验要求：

1.至少实现三种网络模块识别方法。

2.显示PPI网络的模块。

3.计算PPI网络的拓扑特征。

实验步骤：

1.从多个站点下载小型蛋白质互通网络

            HumanNet.txt

2.计算PPI网络的拓扑特征

         节点数：1275

         边数：16288

        平均连通度：25.5498

        聚类系数：0.7051792

        网络密度：0.02005479

        平均路径长度：4.110686

        网络直径：9

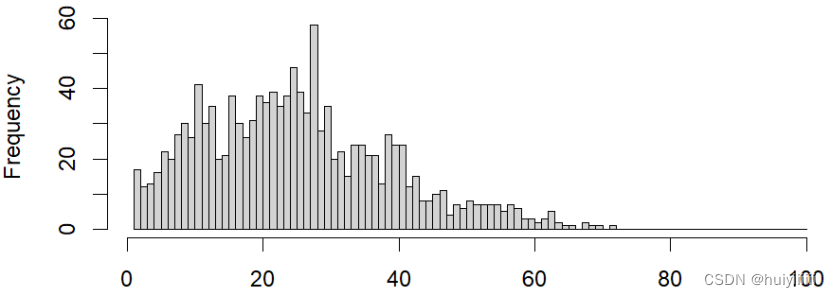
        节点连通度分布：

3.实施3种以上的网络模块识别算法， 并使用这些算法来识别重要的蛋白质网络模块

随机步入算法：cluster_walktrap：

贪婪算法cluster_fast_greedy：

GN算法 cluster_edge_betweenness：

4.编写标记为重要的网络可视化程序网络中的功能模块

5.比较基于不同算法的模块，并分析实验结果不同的原因 

聚类运行时间分析：

   在运行相应的聚类函数时对时间进行记录，结果如下：

   cluster_walktrap= 0.4019232 s 

   cluster_fast_greedy= 0.0344429 s 

   cluster_edge_betweenness= 288.43704 s

设图的顶点数为n，边数为m：

随机游走算法：时间复杂度O(n^2logn)。随机游走算法计算时间为O(mnH)，其中H为相应树状图的高度。最坏的情况是O(mn^2)。但是，大多数现实世界的复杂网络是稀疏的(m=O(n))，并且，H通常很小，并且趋向于树状图平衡的最有利情况(H=O(logn))。在这种情况下，复杂度是O(n^2logn)。

Fast greedy算法：时间复杂度O(n(logn)^2)。在具有n个顶点和m个边的网络上的运行时间为O(mdlogn），其中d是描述群落结构的树状图的深度。许多现实世界的网络都是稀疏和分层的，m=O(n)，d=O(logn)，在这种情况下，fast greedy算法基本上以线性时间O(n(logn)^2)运行。

GN算法：时间复杂度O(m^2n)。GN算法计算边界数的时间复杂度为O(mn)，总时间复杂度在m条边和n个节点的网络下为O(m^2n)。

由于O(m^2n)> O(n^2logn)> O(n(logn)^2)，故三种算法最快的是Fast greedy算法，其次是随机游走算法，最慢的是GN算法。

聚类模块数量分析：

       随机游走算法：根据参数step的不同，聚类模块数量最多时为80，最小时为17。部分对应关系如下：

Step	1	2	3	4	5	6	7	8	9
Num	80	47	33	25	17	20	19	20	19

可以看出基本上随机游走算法的step越小，聚类模块的数量越多，但这种关系不是绝对的，例如当step=5时，聚类模块的数量比步数大的还少。

Fast greedy算法：R语言中cluster_fast_greedy算法没有控制聚类模块数量的相关参数，该算法将网络分为11类。

GN算法: R语言中cluster_edge_betweenness算法没有控制聚类模块数量的相关参数，该算法将网络分为23类。

上述三种算法中Fast greedy算法与GN算法只有一种结果，无法控制聚类数量；而随机游走算法可以通过调节参数step的大小进而控制聚类数量，可以通过控制step的大小粗略控制聚类模块数量，但无法准确的控制。

模块度分析：

  随机游走：0.8675378   Fast greedy：0.8226374   GN：0.8698903

  可以分析出三种聚类算法的模块度均高于0.85，聚类效果很好。其中GN算法的模块度最大，随机游走算法其次，Fast greedy算法最低。

各社区分析：

  随机游走算法：

Id	顶点数	边数	聚类系数	网络密度	平均路径长度	网络直径
1	75	1088	0.7867498	0.3920721	2.01982	6
2	324	2507	0.5635691	0.04791117	3.243282	8
3	144	1887	0.6232384	0.1832751	2.228827	5
4	80	676	0.6131248	0.2139241	2.317405	6
5	58	662	0.8161668	0.400484	1.751966	4
6	44	572	0.7999752	0.6046512	1.491543	4
7	129	2180	0.7638469	0.2640504	2.074612	5
8	27	243	0.9158919	0.6923077	1.410256	3
9	35	318	0.8390617	0.5344538	1.598319	4
10	52	689	0.826532	0.5196078	1.69457	5
11	71	1062	0.685721	0.4273642	1.697384	5
12	48	701	0.7892283	0.6214539	1.425532	4
13	28	299	0.8678269	0.7910053	1.208995	2
14	58	1222	0.8491207	0.7392619	1.261948	3
15	26	325	1	1	1	1
16	47	757	0.7645267	0.7002775	1.299722	2
17	29	406	1	1	1	1

Fast greedy算法：

Id	顶点数	边数	聚类系数	网络密度	平均路径长度	网络直径
1	232	3087	0.6668818	0.1152038	2.8814	8
2	337	2769	0.5928447	0.04890844	3.284672	7
3	107	987	0.6631464	0.1740434	2.436255	5
4	47	730	0.7673873	0.6753006	1.340426	3
5	48	669	0.8033879	0.5930851	1.484929	4
6	31	408	0.9973615	0.8774194	1.182796	3
7	44	544	0.7931336	0.5750529	1.540169	4
8	73	969	0.6801248	0.3687215	1.92618	6
9	87	1484	0.8457853	0.3966854	2.046779	5
10	84	1014	0.8426601	0.2908778	2.244119	4
11	185	2911	0.7632944	0.1710341	2.526792	7

GN算法：

Id	顶点数	边数	聚类系数	网络密度	平均路径长度	网络直径
1	66	373	0.6679178	0.1738928	2.531935	6
2	79	1101	0.7804871	0.3573515	2.165531	7
3	168	1537	0.6090893	0.1095666	2.629099	6
4	71	1066	0.6841199	0.4289738	1.651911	4
5	84	1014	0.8426601	0.2908778	2.244119	4
6	59	713	0.8100615	0.4167154	1.922268	6
7	24	108	0.7319885	0.3913043	1.826087	5
8	76	670	0.6134454	0.2350877	2.143158	5
9	14	53	0.6987342	0.5824176	1.450549	3
10	29	301	0.8619455	0.7413793	1.268473	3
11	90	933	0.5167477	0.2329588	2.050936	5
12	67	937	0.7617906	0.4237901	1.735414	5
13	26	240	0.9169197	0.7384615	1.316923	3
14	9	26	0.7769784	0.7222222	1.277778	2
15	119	2133	0.7668013	0.3038029	1.912833	4
16	54	730	0.7681573	0.5101328	1.577918	4
17	11	32	0.6705882	0.5818182	1.418182	2
18	59	1224	0.8485692	0.7153711	1.300994	3
19	35	318	0.8390617	0.5344538	1.598319	4
20	15	51	0.7522124	0.4857143	1.752381	5
21	47	757	0.7645267	0.7002775	1.299722	2
22	44	572	0.7999752	0.6046512	1.491543	4
23	29	406	1	1	1	1

交叉分析：

  随机游走算法与Fast greedy算法：

随机游走算法与GN算法：

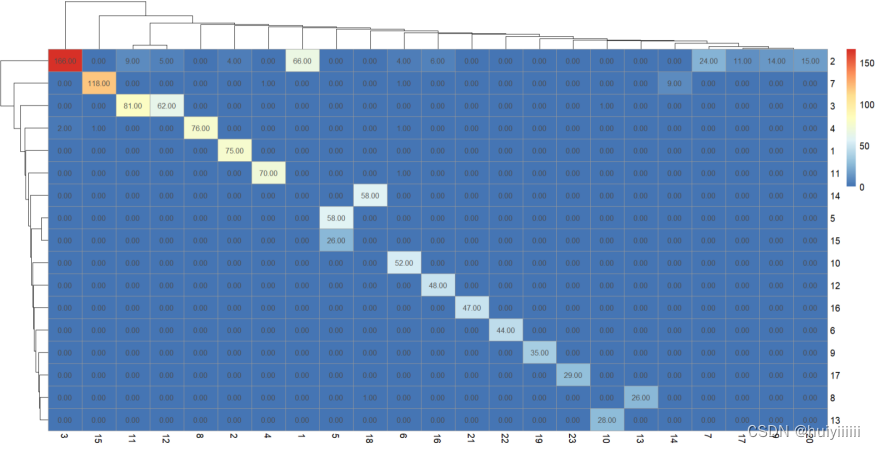
Fast greedy算法与GN算法：

在本网络中，三种聚类方法的模块重叠度很高。随机游走算法，Fast greedy算法与GN算法在计算时均以模块度作为聚类算法结束的标准，即三种算法均追求模块度的最大化划分。其中GN算法开始以整个图为一类，计算各个边介数的大小，再不断将最大边介数的边去除来进行聚类。而随机游走算法与Fast greedy算法开始以每个节点为一类，利用层次聚类进行聚类；随机游走算法通过概率转移矩阵定义各类之间的距离，不断将距离最小的两个类别进行合并；Fast greedy算法利用模块度的增量，不断将模块度增量最大的模块进行合并。

参考代码：

rm(list=ls())
library(igraph)
data<- read.csv("HumanNet.txt",header = TRUE,sep ="\t")
g<-graph.data.frame(data,directed = FALSE)
start<-Sys.time()
c1<-cluster_walktrap(g,step=5)
end1<-Sys.time()
runningtime<-end1-start
print(runningtime) 
c2<-cluster_fast_greedy(g)
end2<-Sys.time()
runningtime<-end2-end1
print(runningtime) 
c3<-cluster_edge_betweenness(g)
end3<-Sys.time()
runningtime<-end3-end2
print(runningtime) 
##节点数
V(g)
##边数
E(g)
##计算平均连通度
sum(degree(g))/length(V(g))
##计算聚类系数
transitivity(g)
##计算网络密度
edge_density(g)
##计算平均路径长度
average.path.length(g)
##计算直径
diameter(g)
##度分布
hist(degree(g,mode="all"),breaks=1:100)

##画图
c<-c1
modularity(c)
#plot(c,g)
V(g)$label=NA
V(g)[degree(g)>=600]$label=V(g)[degree(g)>=600]$name
V(g)$size=4
V(g)[degree(g)>=600]$size=15
mem.col<-rainbow(length(unique(c$membership)),alpha=0.5)
V(g)$color<-mem.col[c$membership]
pdf(paste("C:/Users/86136/Documents/R/lab","/1.pdf",sep=""))
plot(g,layout=layout_with_fr,vertex.color=V(g)$color,
     vertex.laber=V(g)$label,vertex.size=V(g)$size)
dev.off()

##聚类模块数量
c<-c1
length(table(c$membership))

c<-c3
modularity(c)

##各社区节点与边数量
c<-c3
for (i in 1:length(table(c$membership))){
  nodes <- V(g)[c$membership == i]
  g1 <- induced_subgraph(g, nodes)
  cat(i,'\t',length(V(g1)),'\t',length(E(g1)),'\t',
      transitivity(g1),'\t',edge_density(g1),'\t',
      average.path.length(g1),'\t',diameter(g1),'\n')
  plot(g1, layout = layout_with_fr,main=i)
}

library(pheatmap)
a<-table(c1$membership,c2$membership)
pheatmap(a,display_numbers = TRUE)
b<-table(c1$membership,c3$membership)
pheatmap(b,display_numbers = TRUE)
c<-table(c2$membership,c3$membership)
pheatmap(c,display_numbers = TRUE)
d<-table(c1$membership,c2$membership,c3$membership)
pheatmap(d,display_numbers = TRUE)