数据库

数据库之路——

从关系演算到数据立方

作者：WangQingDa                Gender: Male

e-mail：expectoneday@hotmail.com

专业：会计电算化（bachelor）；计算机软件理论（Master）

仅以此文献给我自己，以及对数据库理论和实践感兴趣的并具备足够的耐心阅读它的诸位朋友。数据库对于任何学习计算机专业的人来说都是基础之中的基础，但同时DBMS理论又博大精深，包罗万象，既有深层上的理论研究价值，于实用又可千变万化，解决问题。这份材料主要是作为备忘来编写，也有自己的一些体会性的内容。

 

 

 

 

 

 

 

Bibliography

[1] Jeffery D. Ullman “Principles of DataBase and Knowledge-Base System”

[2] Jiawei Han, Micheline Kamber “Data Mining: Concepts and Techniques”

[3] M.H.Alsuwaiyel （沙特）算法设计技巧与分析

 

1 数据库系统的数据模型理论

什么是数据模型，如果需要让计算机存储并处理数据，那么数据一定要按照便于表达、便于处理、便于应用的模式存储，并有一套相关的理论作为支撑。

Ullman给出了数据模型的定义，虽然比较泛化，抽象，但做到了高度概括：

①  一套标记数据的符号系统，可以描述论域中的所有的数据。

②  一套定义在这个符号系统之上的运算（操作）集，用于处理数据。

1.1 关系模型（Relation Model）

关系模型是由E. Codd在1970年提出来的，它迅速地流行起来并得到了应用，主要是它的Value-oriented（面向值的）特点及对于数据的虽然很简单但是却描述性很强的表达特点。我们可以把数据存储为关系Relation，并且对于定义在关系之上的运算，其结果也是关系，所以利用关系及关系上的运算（operation），我们可以生成一个封闭的代数系统。听起来稍微有些复杂，实际上很简单，大意是你可以把关系模型就理解为一个数据表，关系操作即直接操纵数据，数据处理完之后还是数据表。除了关系模型之外，还有面向对象模型、面向逻辑模型等等。

应该说关系模型是最简单的了，SQL语句是基于关系模型的，否则如果让你写谓词逻辑公式求解数据，那就麻烦透了，数据库用户起码得缩减掉90%。

面向对象的数据模型（如IBM公司推出的ORDBMS），就不如关系模型来得简单，原因可以介绍两条：

①  关系模型便于表示数据处理的结果。因为关系模型不用支持object ID（如果是对象模型，需要为每一个对象类指示ID，并且保证ID不可重复）。

②  支持抽象数据类型的模型，会带来另外的弊端。一个有用的数据库操作往往会产生一个新的数据类型，而这个新的数据类型在系统中需要为它作新的定义，所以这个新的数据类型（临时结果集）无法马上成为一个新的运算操作的操作数。这个问题我个人认为在关系数据库（RDBMS）中也是存在的，除了利用非核心的如Foxpro中的远程视图、C#.net中的内存数据表对象、微软的DTC以外，对关系表的中间计算结果实际上也无法作为下一个关系运算的操作数进行使用。

1.1.1 关系的基本概念（基于集合论的概念表述）

数据库系统中的关系，是取自于集合论中的概念，一个关系，是若干个值域的笛卡尔乘积的子集。

▲域D（domain）：也是一个很宽泛的概念，如整数、实数、有理数、无理数、副点数、双符点、字符、字符串、可变长字符串、大文本、图像、声音、复杂数据类型、对象数据类型等等。

▲ 笛卡尔积╳（Cartesian product）：k个域D₁、D₂、D₃、…D_k的笛卡尔积可以表示为一个k元元组（tuples）的集合，笛卡尔乘积的运算符号为╳，则笛卡尔乘积可以表述为：

D₁╳D₂╳D₃╳…╳D_k={(v₁, v₂, v₃…v_k)|all v₁∈D₁ and v₂∈D₂ … and v_k∈D_k}

▲一个定义在D₁╳D₂╳D₃╳…╳D_k上的关系R也是一个n元组集合，且RÍ D₁╳D₂╳D₃╳…╳D_k。关系R的一个例子是{(0,a),(0,b),(1,c)}，又如{(“Mary”,32),(“Tom”,34)}

▲一个关系的成员称为tuple，即元组。一个关系如果是定义在D₁╳D₂╳D₃╳…╳D_k之上的，则称k为元数（在数据仓库中叫做维度）。一个有着k元数的元组被称为k元组。

□ 评述：这些理论都是非常直观的，所谓的Relation，我们可以理解为一张数据表；所谓的元组，就是数据表中的某一行；没有相关性，没有任何关系的一张表是不可能放在一起的，所以称这个集合为关系。

关系是定义在域的集合之上的，引入域（Domain）的概念，引入域的概念的目的是为了对关系作规范、作限制；甚至可以说域的笛卡尔积形式就是关系的元数据（metadata），它是用来解释关系的模型的。如一个学生档案关系可以是如下笛卡尔积的子集（subset）：全体学生姓名╳地址╳所有电话号码╳大于0小于200的整数╳…。通过指定关系的笛卡尔积的子集形式，我们可以得到关系的模式。但在实际的RDBMS中，域的类型实际上只限于数据类型，而无法对具体的贴近实际应用的域作定义，而辅助以域的名字作为元数据，即通过{域名，数据类型}的方式制定一个域。

□如何对多个关系求笛卡尔积，如何看到在一个关系中所有域的笛卡尔积？

1、对多个关系R₁，R₂，…R_k： SELECT * FROM R₁ ， R₂ ， …R_k

2、对一个关系R中所有域v₁，v₂，…v_K的笛卡尔积

SELECT R₁. v₁ ， R₂. v₂ ， … ， R_K. v_K ，  FROM R R₁, R R₂, … R R_K

即把这一个关系表虚拟成多个（有多少个域，就有多少个虚拟关系），然后分别从不同的数据表中提取出相应的数据域进行笛卡尔积。实际上RDBMS只对多个Relation作笛卡尔积，而不对一个关系表里面的多个字段作笛卡尔积。

□ Example 1.1.1.1：（MS SQL Server）

SELECT R1.admin_id, R2.admin_name, R3.admin_pwd

FROM admin R1 CROSS JOIN admin R2 CROSS JOIN admin R3

这个例子是在 Microsoft SQL Sever 2000 中做出的， Cross Join 表示要对两个关系进行笛卡尔积。

□ Example 1.1.1.2：（Oracle 8）

Select R1.swjg_mc, R2.swjg_jc from ht_swjg_dmb R1, Ht_swjg_dmb R2

 

在 Oracle 中，可以直接去掉关联条件，即可以实现笛卡尔积。

从直观上看，我们似乎很难找到笛卡尔积的实用意义——特别是在具体的应用领域中，但笛卡尔积对于一个 RDBMS 系统至关重要，因为我们所有的对于多个关系表的操作（关联、筛选等等）都是先对多个 RELATION 执行笛卡尔积操作，然后在笛卡尔积上再执行选择（通过 Where 条件做），投影。笛卡尔积是一个数据的操作的上缺界。

□ 以数据表的观点来看关系

模式->	属性	属性	属性	属性	属性	属性	属性
记录	Name	Id	Gender	Address	post	Age	salary
记录	***
记录	***
***	***
***	***

1.1.2 用集合论和映射的观点来理解关系

在我们已经给每一个属性都起了名字的前提下，关系的模式，即字段名的集合的前后顺序就显得无关紧要了。我们也可以把元组看作是从域向属性的映射。这里的观点实际上是设定一个元组变量 µ，然后这个映射实际上是一个一对多的映射，即由一个元组映射到多个属性的值。

□  Example 1.1.2.1

给定一个关系 {City,State,Pop} ： { （ San Diego,Texas,4490 ） ,  （ Miami,Oklahoma,13880 ） , （ Pittsburg,lowa,509 ） }

如果从映射来说，可以理解为对每一个元组集的成员，单个元组，这个一对多的映射 µ,把每一个元组都映射到每个域的某个成员。如对元组 （ San Diego,Texas,4490 ）来说，这个映射可以反映（定义）为：

µ (City)=Diego  ：当前元组对应的 City 域的值是 Diego ；

µ (State)=Texas  ：当前元组对应的 State 域的值是 Texas ；

µ (Pop)=Diego  ：当前元组对应的 Pop 域的值是 4490 ；

当需要按照固定序列列出的时候；当只需要用映射的方式给出时；我们会采用不同的方法。关系表的模式是和顺序相关的，而映射的方式（ set-of-mapping ）是和顺序无关的。在 Set-of-list （即列明字段的模式下，基于集合论 set theory 模式下），我们给出了隐式的强制性的数据列出顺序。

在一个商用的关系型数据库系统中，我们很难说出某个数据库系统是按照集合的模型还是按照映射的模型来处理数据的。比如要在数据库中插入一条数据记录，如果不指名字段的出现顺序， insert into table values (V₁,V₂,…,V_n) ，则就是按照 Set-of-list 处理的数据，而如果使用 insert into table(Attr₁,Attr₂,…,Attr_n) values (V₁,V₂,…,V_n) 插入一条数据记录，则是按照 Set-of-Mapping 的模型处理数据。

1.1.3 把实体-关系模型存储到关系模型中去

实体 - 关系模型，即 Entity-Relation(E-R) 模型，实体关系模型在结构化的软件工程时代（ 1976 年提出）支撑软件工程逻辑建模的基础性工具，到目前仍在不断地完善，发挥实用价值。到后来的 UML 的类图，实际上还是在 E-R 模型之上加入了类的概念，加入了继承、 isa 关系、复杂对象、成员函数等等。

Figure 1.1.3.1  实体关系图

在实体 - 关系图中，每一个实体（图中的大方框中）可以看作是一个关系，一个元组的集合，图中的实体的属性可以看作关系中的域。通过 E-R 图，我们可以把现实世界中的事务虚拟成 E-R 图中的实体、属性，实体之间的关系可以通过图中的连线体现（在关系中体现为具有相同的域），两个抽象实体之间具有共同的属性。而两个抽象实体之间的关系可以体现为一对一、一对多、多对一、多对多。如图 1.1.3.1 种，又两个相关联的抽象实体，一个为学生实体，另一个是成绩实体，两个抽象实体之间通过 Student_ID 建立起关联。注意，这里还存在一个引用关系（ Reference 或称为 ForeignKey ），即学生成绩实体中的学生属性是通过学生号参照的学生档案主关系中的学生号，作为外键，它一定是标志某个实体的关系的主键。这里非常容易理解，因为学生号不可能唯一地表示学生成绩，它只从一个侧面说明了该成绩属于哪个学生。

Figure 1.1.3.2  类图：部门 - 雇员类图

UML （统一建模语言）标准中的类图比 E-R 图多出了什么呢？首先里面确定了继承关系（即 IsA 关系），如图 1.1.3.2 中， Employee is a Person ，即雇员是一个人，没有继承关系的类之间存在着 E-R 关系。而在类图中，还有一种成员变量之间的关系，如轮胎是汽车的一部分，如下图中显示出的汽车和轮子的聚合关系。详细的内容请阅读 UML 文档。

Figure 1.1.3.3

我们甚至可以说， E-R 图是简单化了的类图，或者称 E-R 模型是 Class Diagram 的一个子集。去掉了继承关系，聚合、接口、成员方法、构造函数、析构函数等等，单纯表述出实体之间的静态关系。

1.1.3.1 把E-R图转换为关系模型Relational Scheme

我们使用关系模型集合来表示数据的方法称为关系型数据库模式（ Relational Database scheme ），但我们应该遵循何种方法来使用关系模型呢？通常存在着标准的模式，即先用实体 - 关系模型建模，然后把 E-R 图存储为关系模型，定义在关系型数据库里。

□首先，作为 E-R 图中的一个抽象实体 E ，直接对应于关系模型中的一个关系，该关系的逻辑模式包含了 E 的所有的属性。该实体的实体集可以存储为关系表，即实体集中的每一个具体的实体对应于关系的每一个元组。如果在用关系 R 表示 E 的同时，也要保存其它的实体集 F ，则也需要纳入 F 的属性。

□ 如果需要一个关系 R 表示多个实体集 E₁, E₂, … E_k 之间的联系，则关系 R 的属性集里一定要包括每个实体集的关键字，如果这些实体之间存在着多个重名的字段，则需要修改重复的字段名。

对于“关系”，在数据库的处理中有默认隐含的关系和显示地定义两种：

□  Example 1.1.3.1.1  显式的关系

两个实体集： Employee(em_id,name,age,major,dep_id)

        Department(dep_id,name,responsibilty)

在这个例子中，有两个实体集，一个是雇员集，一个是部门集。在这个实体 - 关系模型中，雇员与部门之间存在着多对一的关系，这种关系我们没有单独用一个关系表（ Relation ）进行存储。因为在雇员关系表中，有一个属性已经能够明确表明这种映射，不用单独建立一个映射关系表了。

□  Example 1.1.3.1.2  隐式的关系

三个实体集： Student(Enroll_id,name,age,major,HomeTown,IdenCo)

        Course(Course_id,description,Teacher,aim,Hours)

   ElectCourse(Enroll_id,Course_id,Year,Term,Score)

在这个例子中，我们注意到 E-R 模型中存在着 3 个实体集，但只有两个真实的静态的实体集，一个是学生实体集，另外一个是课程实体集，实际上在 E-R 图上我们能够见到的也就是这 2 个实体集。我们注意到这两个实体集之间的关系是多对多的关系，即一个学生可以选择多个课程，同时一个课程可以由多个学生选择。由于目前的关系型数据库是一个二维（ 2-dimensional ）结构，不支持在一个单元中继续存储关系，所以对这种多对多的关系必须分解成一对多（或一对一）的关系。所以我们必须显示地分解，即引入选课关系 electCourse ，记录下每一个学生的具体选课情况。

□     从实体关系模型到关系模式如果需要，可以做优化工作。

我们没有必要原封不动地，照本宣科地把实体 - 关系模型中的实体集机械地转换成关系模型，有时候可以合并若干实体集，还有的时候需要把一个实体集分解为多个。这一工作需要考虑数据库的范式理论，即 1NF,2NF,3NF,BCNF 等等。关于范式理论请参阅相关的资料 ; 同时还要考虑系统的运行效率、可移植性、开发成本等等相关的因素。

1.1.3.2 关系中的键（Keys of Relation）

象实体集一样，关系里也要有键。键的概念有些像人的 DNA ，又像是身份证号，象一个企业工商登记证号、组织代码证号，它唯一地表示某个元组（实体）。我们给出键的形式化的概念，关系 R 的键是一组属性 S ，满足：

① 关系 R 中反映现实世界中的实例（以单个元组体现），没有任何两个实例在关系 R 中具有相同的 S 值（即 S 中的每个属性值都相同）。

② 在 S 中去掉任何属性，都无法保证条件 ① 的成立。

键的作用，我个人认为主要有这几个方面：首先，关系里面存储的每一个元组是多个域的成员之间的关系，如一个雇员档案中的某个雇员的元组，记录的是名字、年龄、地域等等，另一方面，元组本身代表了一个实体，这个实体需要有一个能够标志其唯一身份的特征向量，便于从数据库里增加、删除、修改，否则就无法为单个的实体定位；这也是数据库管理系统的需要，为了保持数据的域完整性（世界上不存在两个完全一样的事物）；另外，为了防止数据的冗余，其它的关系在参照这一关系时（即某个属性引用这个关系），可以使用键，而不用录入这个关系的全部的字段值。

□  Example 1.1.3.2.1

我们用一个例子来看一下键值的约束作用。就如我们看一下选课关系 ElectCourse(Enroll_id,Course_id,Year,Term,Score) ，实际上的键值选择要结合现实世界的应用情况，实情况而定。在通常的情况下，我们认为用（ Enroll_id,Course_id ）即可，即学生、课程可以唯一标志一个选课，不可能存在两条一样的元组，即同一个学生选了两次课（重复学习）；而且去除掉健的任何一个成员，都无法保证键值不重复。同理，（ Enroll_id,Course_id ）作为键，如果加入一个字段，也无法保证其逻辑的可行性（ DBMS 无法控制其逻辑上是否合理，这时允许重复的 Enroll_id,Course_id 对出现在数据库中），如果增加一个键的成员属性，则出现了例如（ Mary,History,78.5 ）和 (Mary,History,86) 的成绩，一门课程同一个人两个成绩，不是很荒谬吗！但这种把键放得太大的情况，要靠设计人员自行控制。

所以我们说，如何对一个关系设计它的键，不是取决于它的数据实例，而是最终取决于整个关系的概念含义，其实际的环境约束。取决于 Scheme 。

□ 多个健值

很多时候在一个关系中，模式定义里有多个键，如对于一个企业档案信息关系，全国统一的组织机构代码可以作为一个键；如果不允许存在同名的企业，则企业的名称也可以作为键。通常情况下， DBMS 希望设计者能够指定一个主键，以便于数据库管理系统从物理存储上便于管理关系表，这个键称作主键， Primary key 。所有具备键的条件的属性集被称为备选键。

 

 

1.1.3.3 关系之间拥有的共同的键

每一个关系都是若干的域的笛卡尔积的子集，关系与关系之间有可能存在着共同的属性，也有可能存在着共同的键（ Common Key ）。即某个健 K ，既是关系 R1 的备选键，又是 R2 的备选键，则 K 成为 R1 和 R2 的共同拥有的键。注意，这里要强调的是仅仅是属性名一致、数据域一致还不能称之为 Common Key ，只有确定语义上的一致才可以，如 Student(Id,name,age) 和 Teacher(Id,graduateTime,Major) ，虽然是都有 id 作为主键，但一个是学生登记号而另一个是教师工号，两个 id 是截然不同的东西，不是共同键。如果语义上一致，即使键的名字或属性的名称不对应，甚至是数据类型不对应，也可以认为是 Common Key ，可以通过其进行管理的连接。

□    如果多个 Relation 之间具有 Common key ，则这多个关系之间可以通过共同键合并为一个关系。这样做的好处之一是可以节省空间；另外，如果某些查询涉及到这多个关系，可以使查询语句变得更为简洁，执行速度更快。

但带来的坏处是把多个实体集合并在一起，使整个关系模式变得含混，失去了清晰的语义，不太符合“分而治之”的原则。

1.1.3.4 空挂的元组（Dangling Tuples）

如果需要对两个拥有 Common Key 关系 R1 和 R2 进行合并成一个关系的操作，则我们注意到如果 R1 和 R2 的 Common key 的值不能做到一一对应，那末会导致 R1 或  R2 中有一些元组无法合并到新的关系中，如下图：

<img alt="" src="http://writeblog.csdn.net/Editor/FCKeditor/editor/%3Chtml%3E%20%20%20%20%3Chead%3E%20%20%20%20%20%20%20%20%3Ctitle%3E%E9%8D%99%E5%82%9B%E6%9A%9F%E9%8F%83%E7%8A%B3%E6%99%A5%E9%8A%86?/title%3E%20%20%20%20%20%20%20%20%3Cstyle%3E%20%20%20%20%20%20%20%20%20body%20{font-family:%22Verdana%22;font-weight:normal;font-size:%20.7em;color:black;}%20%20%20%20%20%20%20%20%20%20p%20{font-family:%22Verdana%22;font-weight:normal;color:black;margin-top:%20-5px}%20%20%20%20%20%20%20%20%20b%20{font-family:%22Verdana%22;font-weight:bold;color:black;margin-top:%20-5px}%20%20%20%20%20%20%20%20%20H1%20{%20font-family:%22Verdana%22;font-weight:normal;font-size:18pt;color:red%20}%20%20%20%20%20%20%20%20%20H2%20{%20font-family:%22Verdana%22;font-weight:normal;font-size:14pt;color:maroon%20}%20%20%20%20%20%20%20%20%20pre%20{font-family:%22Lucida%20Console%22;font-size:%20.9em}%20%20%20%20%20%20%20%20%20.marker%20{font-weight:%20bold;%20color:%20black;text-decoration:%20none;}%20%20%20%20%20%20%20%20%20.version%20{color:%20gray;}%20%20%20%20%20%20%20%20%20.error%20{margin-bottom:%2010px;}%20%20%20%20%20%20%20%20%20.expandable%20{%20text-decoration:underline;%20font-weight:bold;%20color:navy;%20cursor:hand;%20}%20%20%20%20%20%20%20%20%3C/style%3E%20%20%20%20%3C/head%3E%20%20%20%20%3Cbody%20bgcolor=%22white%22%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cspan%3E%3Cdiv%3E%3Cb%3E%3Cfont%20size=%226%22%3E%E9%88%A5?%E9%88%A5%E6%BF%86%E7%B0%B2%E9%90%A2%E3%84%A7%E2%96%BC%E6%90%B4%E5%BF%8E%E8%85%91%E9%90%A8%E5%8B%AC%E6%B9%87%E9%8D%94%E2%80%B3%E6%AB%92%E9%96%BF%E6%AC%92%EE%87%A4%E9%8A%86?hr%20width=100%%20size=1%20color=silver%3E%3C/font%3E%3C/b%3E%3C/div%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cdiv%3E%3Cb%3E%3Cfont%20size=%225%22%3E%20%3Ci%3E%E9%8D%99%E5%82%9B%E6%9A%9F%E9%8F%83%E7%8A%B3%E6%99%A5%E9%8A%86?/i%3E%20%3C/font%3E%3C/b%3E%3C/div%3E%3C/span%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cfont%20face=%22Arial,%20Helvetica,%20Geneva,%20SunSans-Regular,%20sans-serif%20%22%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cb%3E%20%E7%92%87%E5%AD%98%E6%A7%91:%20%3C/b%3E%E9%8E%B5%D1%86%EE%94%91%E8%A4%B0%E6%92%B3%E5%A2%A0%20Web%20%E7%92%87%E9%94%8B%E7%9C%B0%E9%8F%88%E7%86%BC%E6%A3%BF%E9%94%9B%E5%B1%BD%E5%9A%AD%E9%90%9C%E7%89%88%E6%B9%AD%E6%BE%B6%E5%8B%AD%E6%82%8A%E9%90%A8%E5%8B%AB%E7%B4%93%E7%94%AF%E6%90%9E%E2%82%AC%E5%82%9D%EE%87%AC%E5%A6%AB%E2%82%AC%E9%8F%8C%E3%83%A5%E7%88%A2%E9%8F%8D%E5%A0%A3%E7%AA%A1%E9%9F%AA%EE%81%83%E4%BF%8A%E9%8E%AD%EE%88%A4%E7%B4%9D%E6%B5%A0%E3%83%A4%E7%B0%A1%E7%91%99%EF%BD%86%E6%B9%81%E9%8D%8F%E5%AE%A0%EE%87%9A%E9%96%BF%E6%AC%92%EE%87%A4%E6%B5%A0%E3%83%A5%E5%BC%B7%E6%B5%A0%EF%BD%87%E7%88%9C%E6%B6%93%EE%85%9E%EE%87%B1%E9%91%B7%E6%92%AE%E6%95%8A%E7%92%87%EE%88%9C%E6%AE%91%E9%8D%91%E5%93%84%EE%98%A9%E9%90%A8%E5%8B%AE%EE%87%9B%E7%BC%81%E5%97%95%E4%BF%8A%E9%8E%AD%EE%88%98%E2%82%AC?%20%20%20%20%20%20%20%20%20%20%20%20%3Cbr%3E%3Cbr%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cb%3E%20%E5%AF%AE%E5%82%9A%E7%88%B6%E7%92%87%EF%B8%BE%E7%B2%8F%E6%B7%87%E2%84%83%E4%BC%85:%20%3C/b%3ESystem.ArgumentException:%20%E9%8D%99%E5%82%9B%E6%9A%9F%E9%8F%83%E7%8A%B3%E6%99%A5%E9%8A%86?br%3E%3Cbr%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cb%3E%E5%A9%A7%E6%84%B0%E6%95%8A%E7%92%87?%3C/b%3E%20%3Cbr%3E%3Cbr%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Ctable%20width=100%%20bgcolor=%22#ffffcc"> <tr> <td> <code>鍙湁鍦ㄨ皟璇曟ā寮忎笅杩涜缂栬瘧鏃讹紝鐢熸垚姝ゆ湭澶勭悊寮傚父鐨勬簮浠ｇ爜鎵嶄細鏄剧ず鍑烘潵銆傝嫢瑕佸惎鐢ㄦ鍔熻兘锛岃鎵ц浠ヤ笅姝ラ涔嬩竴锛岀劧鍚庤姹?URL: <br><br>1. 鍦ㄤ骇鐢熼敊璇殑鏂囦欢鐨勯《閮ㄦ坊鍔犱竴鏉♀€淒ebug=true鈥濇寚浠ゃ€備緥濡? <br><br>   <%@ Page Language="C" Debug="true" %><br><br>鎴?<br><br>2. 灏嗕互涓嬬殑鑺傛坊鍔犲埌搴旂敤绋嬪簭鐨勯厤缃枃浠朵腑:<br><br><configuration><br>    <system.web><br>        <compilation debug="true"/><br>    </system.web><br></configuration><br><br> 璇锋敞鎰忥紝绗簩涓楠ゅ皢浣跨粰瀹氬簲鐢ㄧ▼搴忎腑鐨勬墍鏈夋枃浠跺湪璋冭瘯妯″紡涓嬭繘琛岀紪璇戯紱绗竴涓楠や粎浣胯鐗瑰畾鏂囦欢鍦ㄨ皟璇曟ā寮忎笅杩涜缂栬瘧銆?br><br>閲嶈浜嬮」: 浠ヨ皟璇曟ā寮忚繍琛屽簲鐢ㄧ▼搴忎竴瀹氫細浜х敓鍐呭瓨/鎬ц兘绯荤粺寮€閿€銆傚湪閮ㄧ讲鍒扮敓浜ф柟妗堜箣鍓嶏紝搴旂‘淇濆簲鐢ㄧ▼搴忚皟璇曞凡绂佺敤銆?/code> </td> </tr> </table> <br> <b>鍫嗘爤璺熻釜:</b> <br><br> <table width=100% bgcolor="ffffcc"> <tr> <td> <code><pre>[ArgumentException: 鍙傛暟鏃犳晥銆俔 System.Drawing.Image.FromStream(Stream stream, Boolean useEmbeddedColorManagement, Boolean validateImageData) +388134 System.Drawing.Image.FromStream(Stream stream) +8 Dottext.Admin.UploadWord.SaveFile(HttpPostedFile File) +32 Dottext.Admin.UploadWord.Page_Load(Object sender, EventArgs e) +76 System.Web.Util.CalliHelper.EventArgFunctionCaller(IntPtr fp, Object o, Object t, EventArgs e) +15 System.Web.Util.CalliEventHandlerDelegateProxy.Callback(Object sender, EventArgs e) +34 System.Web.UI.Control.OnLoad(EventArgs e) +99 System.Web.UI.Control.LoadRecursive() +47 System.Web.UI.Page.ProcessRequestMain(Boolean includeStagesBeforeAsyncPoint, Boolean includeStagesAfterAsyncPoint) +1061</pre></code> </td> </tr> </table> <br> <hr width=100% size=1 color=silver> <b>鐗堟湰淇℃伅:</b> Microsoft .NET Framework 鐗堟湰:2.0.50727.832; ASP.NET 鐗堟湰:2.0.50727.832 </font> </body></html><!-- [ArgumentException]: 鍙傛暟鏃犳晥銆? 鍦?System.Drawing.Image.FromStream(Stream stream, Boolean useEmbeddedColorManagement, Boolean validateImageData) 鍦?System.Drawing.Image.FromStream(Stream stream) 鍦?Dottext.Admin.UploadWord.SaveFile(HttpPostedFile File) 鍦?Dottext.Admin.UploadWord.Page_Load(Object sender, EventArgs e) 鍦?System.Web.Util.CalliHelper.EventArgFunctionCaller(IntPtr fp, Object o, Object t, EventArgs e) 鍦?System.Web.Util.CalliEventHandlerDelegateProxy.Callback(Object sender, EventArgs e) 鍦?System.Web.UI.Control.OnLoad(EventArgs e) 鍦?System.Web.UI.Control.LoadRecursive() 鍦?System.Web.UI.Page.ProcessRequestMain(Boolean includeStagesBeforeAsyncPoint, Boolean includeStagesAfterAsyncPoint)[HttpUnhandledException]: 寮曞彂绫诲瀷涓衡€淪ystem.Web.HttpUnhandledException鈥濈殑寮傚父銆? 鍦?System.Web.UI.Page.HandleError(Exception e) 鍦?System.Web.UI.Page.ProcessRequestMain(Boolean includeStagesBeforeAsyncPoint, Boolean includeStagesAfterAsyncPoint) 鍦?System.Web.UI.Page.ProcessRequest(Boolean includeStagesBeforeAsyncPoint, Boolean includeStagesAfterAsyncPoint) 鍦?System.Web.UI.Page.ProcessRequest() 鍦?System.Web.UI.Page.ProcessRequestWithNoAssert(HttpContext context) 鍦?System.Web.UI.Page.ProcessRequest(HttpContext context) 鍦?ASP.uploadword_aspx.ProcessRequest(HttpContext context) 鍦?System.Web.HttpApplication.CallHandlerExecutionStep.System.Web.HttpApplication.IExecutionStep.Execute() 鍦?System.Web.HttpApplication.ExecuteStep(IExecutionStep step, Boolean& completedSynchronously)--><!-- 姝ら敊璇〉鍙兘鍖呭惈鏁忔劅淇℃伅锛屽洜涓?ASP.NET 閫氳繃 <customErrors mode=" off"="" >="" 琚厤缃负鏄剧ず璇︾粏閿欒淇℃伅銆傝鑰冭檻鍦ㄧ敓浜х幆澧冧腑浣跨敤="" <customerrors="" mode="On" 鎴?<customerrors="" >銆?-="" style="border-top-style: none; border-right-style: none; border-bottom-style: none; border-left-style: none; border-width: initial; border-color: initial; border-image: initial; ">'>1

我们注意到，工商登记和企业登记存在着共同键 企业名称 ，所以我们完全可以把这两个关系合并到一个关系，工商税务登记关系中。但是我们注意到有的企业只办理了工商登记，还没有来得及办理税务登记证，没有统一的纳税识别号，所以也无法向 税务登记证 关系中添加；另外，有些按照法律应该属于纳税人并负有纳税义务的企业并没有办理工商登记，或已经被吊销了工商营业执照但仍持续经营需要继续使用税务登记证键的，无法在工商登记证里添加元组，因为没有营业执照号码。我们把这些需要添加但无法添加的元组称为空挂元组。

□ 空挂元组（ Dangling Tuples ）的定义

在一个关系模型中，空挂元组是这样一些元组：在一个关系 R1 中存在，并且具有某个共同键 Common key 的属性值 v ，按照关系模式，需要在关系 R2 中也存在着这个 Common key 的属性值 v 。但是在关系 R2 中并不存在这个属性值 V ，我们把这样的元组称为空挂元组 Dangling Tuples 。在存在空挂元组的情况下，如果我们根据共同键去合并多个关系，则一定会造成信息的丢失。在实际的应用情况中，我们使用 SQL 语句对两个数据表进行自然连接 ( 使用 inner join 或者使用等于号 = 进行数据表的连接 ) ，也会出现抛弃一部分原始元组的情况。但大部分的情况下，这种信息丢失是我们所希望的，如在图 1.1.3.4.1 中，我们需要查询出既办理了工商登记又办理了税务登记的企业，则这种丢弃是正常的。

那么我们应该如何解决 Dangling Tuples 的问题呢？当然，如果不牵涉到合并关系的话，我们可以忽略这个问题。但是，如果我们不得不把这两个关系合并到一起，为了节省空间的原因，或者其他原因（如 DBMS 中的 object 个数超过了限制）我们必须要合并关系，则一种可能的方法是在数据库的关系模式中加入约束机制（在实际的数据库管理信息系统中可以通过触发器、通过设定字段的默认值、通过 Rules 等方法来实现）。即在关系的合并之前就确保两个具有共同的 Common Key 的关系中的键值是一一对应的，在不存在 Dangling Tuple 的前提下，当然可以自然地把两个关系合并为一个关系。但要求同时写入这两个关系的 common key 于实际应用是不切合的，因为数据库系统就是为了实际应用服务的，而不是反过来单纯为了合并关系。

命题：“ R1 中存在 v 必须以 R2 中存在 v 为前提”和“ R2 中存在 v 必须以 R1 中存在 v 为前提”这两个断言（命题）本身就是矛盾，实用中也无法解决。这个原因也是数据库产生死锁的原因。

    证明：“如果关系 R1 中存在 v ，则 R2 中也一定存在 v ”表示为

R1(v) → R2 （ v ），同时，“如果关系 R2 中存在 v ，则 R1 中也一定存在 v ”表示为

R2(v) → R1 （ v ）。这两个规则要同时成立。 R1(v) → R2 （ v ）等价于～ R1(v) ∨ R2(v) ；同理 R2(v) → R1 （ v ）等价于～ R2(v) ∨ R1(v) 则根据分配率

（～ R1(v) ∨ R2(v) ）∧（～ R2(v) ∨ R1(v) ）可以化简为

～ R1(v) ∧～ R2(v) 或 R1(v) ∧ R2(v) ，即不允许有时间差，不允许为前提。

□     允许空值的属性（ Null value ）

在 Ullman 的《 Principles of DB & KB 》一书中，给出了一种解决问题的办法，即允许合并以后的表存在空的值 null Value 。在图 1.1.3.4.1 中，可以合并成如下的表格：

企业名称	工商登记号	经营地址	纳税号	财务主管
甲	1	胡同口	45661	Mary
乙	⊥	⊥	214555	John
丙	2	大坡	225553	Lion
丁	3	河畔路	⊥	⊥
企业4	4	开发区	⊥	⊥
企业5	5	创业园	⊥	⊥

Figure 1.1.3.4.2

当然，这种方法可以通过允许工商登记证号和税务登记证号为空来解决一个企业的所有工商税务登记信息的存储问题，而且在实用的 DBMS 里设计关系模式的时候（ table designer ）也支持设计者自行选择一个字段的可空 null 或非空 not null 。这样似乎解决了问题，但是我们注意到这个数据表可能在实用中被频繁地检索（合并的关系越多，检索可能就越频繁），这个表的 primary key 很明显只能是企业名称字段，因为只有这一字段能够标示唯一的记录。因为在所有的数据库系统中， primary key 都是要求非空的。我们如果对工商登记证号和纳税识别号建立索引，则会大大降低系统运行效率。

□ 实际上我们完全没有必要处理 Common key ，我们还是分别存储，一方面保证了数据的完整性和精确性，使关系的定义更加清晰；另一方面，现代的商用 DBMS 提供了自然连接、左连接、右连接、全连接等方式提供所需要的视图。如下：

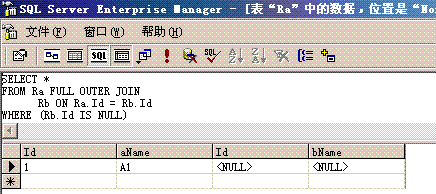
关系 Ra    Id            aName			关系 Rb     Id            bName
1	A1		2	B2
2	A2		3	B3

Figure 1.1.3.4.2  使用 Full outer Join  解决 Dangling Tuples

为了叙述简便，我们把问题精简为两个关系 Ra 和 Rb ， Ra 和 Rb 各自拥有共同键 Id 。并且， Ra 中拥有空挂元组（ 1,A1 ）且 Rb 中拥有空挂元组（ 3,B3 ），通过使用 Full outer join ，自动为空挂元组补齐了合并后关系需要的空值。命令的语句是：

SELECT * FROM Ra FULL OUTER JOIN Rb on Ra.Id=Rb.Id

关系的连接运算我们在下一节当中将会详细地讲解。

 

1.2 关系模型中的运算

上一节我们主要介绍了关系模型，关系模型是数据库最重要的模型，网状和层次模型目前已经基本上失去了商用的市场，目前业界流行的 Oracle 、 Sybase 、 DB2 、 MS SQL Server 等都是基于关系模型的数据库关系系统，即 RDBMS 。有两种形式符号系统可以表示关系模型中的运算：

① 使用代数系统（ algebraic ）作形式化描述，我们称之为关系代数（ relational algebra ）。即要把关系看作操作数和集合，这个关系形成的集合里定义一系列的运算，形成了一个代数系统。关于代数系统的详细的理论、群论、及同态和同构的理论请参阅离散数学书籍。

② 使用形式逻辑，称为关系演算 relational calculus （或称关系微积分）。在关系演算中，所有的对关系的操纵和查询都必须用逻辑运算算式表示，数据的查询结果是那些满足逻辑算式的元组集。 SQL 语句， Structured Query Language ，即结构化的查询语言（ Ansi 标准），就是基于关系演算的，也是目前绝大多数的商用数据库所支持的。

在本章里，我们将主要讲解关系代数，而不主要讲解关系演算。虽然在实际的商用 RDBMS 中，数据是按照元组变量级进行判断，凡是符合元组关系演算约束的，就作为演算结果输出，但由于关系代数比元组关系演算形式上更加直观、关系代数的运算式更加易于理解，我们还是从关系代数开始介绍。但这里我们可以先给出一个元组关系演算的例子。在图 1.1.3.4.1 中，我们要求解那些已经办理了税务登记的工商登记户情况，如果我们使用元组关系演算的话，则逻辑算式应该写成如下的方式：

{ μ | 工商登记（μ）∧ $ υ（税务登记（υ）∧μ [ 企业名称 ]=  υ [ 企业名称 ] ） }

我们看到，这个元组关系演算的算式比较复杂。而如果用关系代数来表示，只需要用一个自然连接运算就可以解决问题。所以，我们先从易入手。

1.2.1 受限的关系代数

我们所选择的关系代数模型，是为了便于数据库的用户和关系交互，而不是和数据的物理存储交互。虽然从道理上讲，我们编写的任何以关系为形参的程序处理模块都是合法的关系代数的算符，但是，另一方面，我们必须把算符集作得足够小，足够规范，否则如果关系代数运算符过于依赖于物理存储模式，会给 RDBMS 和设计者带来很大的不方便。

1.2.1.1 基于过程的关系代数模型和基于逻辑的求解比较

我们在设计一个好的关系代数系统时，一定要保证它的执行效率是高的，我们可以对它的执行去做优化，我们能够预见到某个关系代数的操作的执行效率，在给定的数据量下，我们可以计算出大概的运行时间。我们这里举出一个反例，即 Prolog 语言， Prolog 的优势在于它的逻辑处理能力，在于它能够做出千变万化的求解程序，目前的专家系统基本上是以 Prolog 为工具。但是我们能够直接把关系 Relation 看作是谓词 Predicates ，进而把关系表中的每一个元组都看作是一个命题或断言 proposition ，从而形成一个专家系统呢？当需要在数据库里查询或运算时，由用户写出求解的语句，由自由变量输出查询结果。应该说这样的系统一定是表达力和求解能力最强的数据库系统。 Prolog 是一种面向逻辑的求解系统，而关系代数则是面向过程的， Prolog 的求解过程由计算机控制，用户只要把逻辑表达清楚即可。我们用一个例子来看一下：

Example 1.2.1.1.1  求解兄弟关系

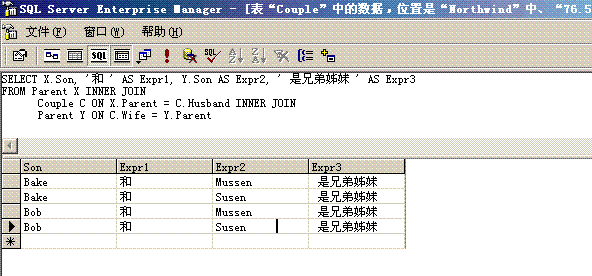
Relation: Parent
Parent	Son
JaSen	Tom
JaSen	Jack
Larry	Bob
Larry	Bake
Batti	Susen
Batti	Mussen

 

Relation: Couple
Husband	Wife
Larry	Batti
…	…

在本例中，有两个关系： Parents(Parent,Son) 和 Couple(Husband, Wife) ，我们的问题是根据这两个关系求解 Brother_Sister 的关系。一个 Prolog 的求解系统主要由两大部分组成，一部分是知识库，另外一部分是产生式规则。对于一个用 Prolog 语言求解的系统来说，针对这个问题要做如下工作：

    首先，要把关系中的每一个元组都表示成知识库的形式，即描述事实性的子句 Clause ， Prolog 把关系名自动转换为谓词 predicates ，把数据库的每一条记录都转换为不含有任何变量的子句，如下：

Parent(JaSen,Tom).

   Parent(JaSen,Jack).

   Parent(Larry,Bob).

   Parent(Larry,Bake).

   Parent(Batti,Susen)

   Parent(Batti,Mussen).

   Couple(Larry,Batti).

    然后，需要由数据库的用户编写产生式规则，也就是逻辑推理的知识，形式是“如果 A 条件满足，则我们断定 B 成立”，形式是“ B:-A. ”。在这个例子中我们可以定义兄弟姊妹关系：

Brother_Sister(X,Y):-Parent(CParent,X),Parent(Cparent,Y).

这个规则用文字可以描述为“如果在 Parent 关系中存在一个人 Cparent ，并且这个人是 X 的生父（母），又是 Y 的生父（母），则 X 和 Y 是兄弟姊妹”。用形式逻辑中的谓词逻辑表达则是：

$  Cparent Parent(Cparent ， X)  ∧  Parent （ Cparent ， Y ）→ Brother_Sister(X ， Y)

这个问题的求解方式也很简单：

goal

       Write(X ，“和”， Y ，“是兄弟姊妹。” ) ， Brother_Sister(X ， Y).

详细的基于逻辑的数据库请阅读 Prolog 书籍和知识库书籍。

可能很多朋友认为这个问题就万事大吉了，“这个问题很简单吗！拥有相同的父母不就是兄弟姊妹了吗”。这正反映了 Prolog 求解的难点所在，即用 Prolog 求解一定要保证知识和规则的完备（ Complete ），不能有缺失，也不可有冗余，否则会“失之毫厘，谬以千里”。在 Parent 关系中，对于一个子女，可能只存在 着 父亲或母亲的信息，而没有充分利用夫妻关系进行问题的求解，很有可能对于一对兄弟， Parent 表中只有兄的父亲信息和弟的母亲信息，但这个查询无法查出，因此，我们还需要补充规则。

Brother_Sister(X,Y):-Couple(Husband,Wife),Parent(Husband,X),Parent(Wife,Y).

我们看到，用逻辑求解虽然表达能力强，但规则的编写具有一定的难度，如果这个问题需要我们用面向过程的语言求解，如用 SQL 语句求解，可以如下：

对于 Brother_Sister(X,Y):-Parent(CParent,X),Parent(Cparent,Y).  我们可以写出如下的 SQL 语句：

Select X.Son,” 和 ”,Y.Son,” 是兄弟姊妹 ” From Parent X, Parent Y where X.Parent=Y.Parent

对于规则：

Brother_Sister(X,Y):-Couple(Husband,Wife),Parent(Husband,X),Parent(Wife,Y).  我们可以写出如下的 SQL 语句：

SELECT X.Son,” 和 ”,Y.Son,” 是兄弟姊妹 ”

FROM Parent X, Parent Y, Couple C where

X.Parent=C.Husband and

C.Wife=Y.Parent

Figure 1.2.1.1.1  第二条产生式规则等价的 SQL 语句

最终我们看出，无论是用关系代数模型还是用基于形式逻辑的模型，本质上都是一样的，即叙述清事实情况，即把数据存储好；另一方面描述清楚逻辑关系，对于用 SQL 语言求解的情况，还要把求解的思路弄清楚。我们看到 Prolog 和 SQL 在关系模型上求解问题各有优劣。 Prolog 比较擅长于逻辑性强的问题求解， SQL 擅长基于过程的求解，可以看到阶段性的结果，便于修正、补足求解策略。

学过形式逻辑的朋友知道，图灵机存在着一个图灵停机问题，而一般意义上的 Prolog 语言是图灵机的等价，所以也存在着 Prolog 程序的停机问题。我们无法预知一个 Prolog 程序何时能够停下来，给定一些关系数据和一段 Prolog 程序，我们无法预知它何时能够停下来。所以，我们必须对关系之上的标准操作作限定，即我们要在实用中使用限定了的关系操作。

1.2.1.2 关系代数中的操作符和操作数

下面，我们就着重讲解在关系代数模型中的操作符（ Operators ）和操作数（ Operands ）。在关系代数里，关系是由 k 元组组成的， k 元组的每一个成员都有一个隐含的属性的名字。由于我们在这里不是用映射来表示，所以强制要求元组的成员前后顺序是有关的，即各个字段要按照预先设计好的顺序出现。那么如果对一个给定关系表的关系模式作一下调整，改变一下字段的顺序，是否会影响程序的运行呢？我们回想一下各种开发工具对数据库的读取操作，对某些开发工具或某个开发工具的某个数据读取方法，顺序是重要的，我们需要使用类似于读取数组数据的方法来读取当前元组的某个下标的数组数据。如我们使用 Asp 或 Asp.net 开发数据库应用系统，当检索出数据结果时，既可以直接用下标，也可以用返回的属性名（注意 SQL 语句在投影时，可以改变属性的名称），如：

Asp 中用顺序号引用数据	Asp.net 中用属性名引用数据
Set RS=newconn.Execute(SQLcmd) For i=0 To RS.Fields.Count-1 =RS(i)     Next	While(DataReader.Read()) { int myAge=DataReader.GetInt32 (DataReader.GetOrdinal(“age”)) }

Figure 1.2.1.2.1  对数据查询结果的访问

这是因为目前随着数据库的发展，数据字典或称元数据的技术也在不断地发展。当我们检索数据的时候，不仅能返回元组集，同时也能返回关于这些元组集数据的描述。我们可以用程序去读取这些描述，然后有针对性地处理数据。标准的关系代数运算一共有个：联合（ union ）、求差集（ difference ）、求笛卡尔积（ Cartesian ）、投影（ Projection ）、选择（ Selection ）。下面，我们逐一讲解这 5 个运算，并辅以 SQL 语句作为等价的表达。

1.2.1.2.1 联合（Union）

联合操作也就是对两个关系的求并运算的操作，对给定的两个关系 R 和 S ，如果两个关系的关系模式相同，则可以执行对两个关系的求并操作，即使两个关系的对应的属性名不相同，只要域（数据类型）相同即可，表示为 R ∪ S 。在 MS SQLServer 2000 中，我们对图 Figure 1.1.3.4.2 中的两个关系 Ra 和 Rb 作了测试， Ra(Id int,aName char(10))  和  Rb （ Id int,bName char(12) ），两个关系的属性名不是完全一致，而且字符串的长度也不一致，但能够进行联合运算。但如果把 Rb 的关系模式的顺序颠倒一下，即 Rb(bName char(12),Id int) ，运行求 Union 的语句就会报错。　　

□  select Id,aName from Ra Union (select Id,bName from Rb) √ 

□  select Id,aName from Ra Union (select bName,Id from Rb) ╳

我们形式化地给出两个集合的并集的定义：

R ∪ S={u|u ∈ R or u ∈ S) and R has the same scheme of S }

1.2.1.2.2 差集（Set difference）

两个集合 R 和 S 的差集可以表述成表述成 R-S ，其运算结果也是一个与 R 和 S 同结构的两个集合，其成员是属于 R 但不属于 S 的元组的集合。在实际的 RDBMS 系统中求差集没有给出具体的命令来实现。但我们可以给出形式化的定义：

R-S={u|u ∈ R  ∧ ～ (u ∈ S)}

1.2.1.2.3 投影（Projection　）

投影操作是对一个给定的关系去掉若干属性，对一个 k 元组的关系 R 来说，如果我们想留下第 i₁ ， i₂ ， i₃ … i_m ，（ m<=k ）个属性，则我们可以把不在这些属性列表里的属性（字段）去掉。投影运算可以表示为 π i₁ ， i₂ ， i₃ … i_m （ R ），我们也可以直接使用属性名作为投影的字段，如 π _1,4,6 （ Profile ），即可以把个人档案中的姓名，住址，年龄三个属性提取出来，形成一个新的关系。而且在投影的时候，我们还可以把属性出现的前后顺序颠倒一下。对 R 关系， Name, Address ， Age 在元组中按照既定的顺序出现，我们可以把这个顺序颠倒或打乱一下，如： π _{Adress, Name,Age} （ Profile ）也是一个合法的投影。

投影运算可以使我们 : ① 只得到我们必需的信息，忽略掉冗余的信息。 ② 让使用关系的用户按照自己希望的顺序重新排列元组的顺序。 ③ 投影运算结束后，还会去掉重复的元组，因为理论上的数据库认为世界上不会存在完全一模一样的两个实体。但这和实际的商用 DBMS 有些差别，在实际使用的商用 RDBMS 中系统不会自动地去除重复的元组（即两个一模一样的元组）。如果用户需要去掉重复的元组，可以在投影的同时使用 Distinct 关键字把重复的元组去掉（如下图）。

如果我们不使用 Distinct 关键字约束，目前商用的 RDBMS 不会自动去掉重复的元组，因为有可能丢失有用的信息。　

1.2.1.2.4 笛卡尔积（Cartesian Product）

在前面我们已经介绍了多个域之间的笛卡尔积的定义，下面我们介绍两个关系之间的笛卡尔积运算。关系 R （ U₁,U₂,… U_m ）和 S （ V₁,V₂,… V_n ）的笛卡尔积是一个 m+n 元组的集合，可以形式化地定义为：

R × S={( u₁,u₂,… u_m,v₁,v₂,… v_n)| all possible (u₁,u₂,… u_m) ∈ U and  （ v₁,v₂,… v_n ）∈ V}

即 R 和 S 的笛卡尔积是一个 m+n 元组集合，每一个元组的前 m 元都是 R 的成员，其后 n 元都是 S 的成员。对于理论上的关系代数，由于 R 中和 S 中都没有重复的元组，所以 |R × S|=|R| × |S| ，即 Number(R × S)=Number(R) × Number(S) 。但是在实用的应用中，在一个关系中出现完全相同的元组是很正常的事情，因为一个关系不仅要记录实体，还要记录事务、事件等等。在实际的 RDBMS 里是怎样处理笛卡尔积的呢？我们用过程描述语言表达如下：

CartesianOfRelations(relation R, relation S)

// 参数是 R 和 S 两个关系

{

   Relation RS;

   RS=new (Relation); // 新建立一个新的关系的引用，用来存储笛卡尔

运算以后的结果

   RS.attributes.append(R.attributes);

        //  把关系 R 的所有的属性都增加到 RS 中

   RS.attributes.append(R.attributes);

        //  把关系 S 的所有的属性都增加到 RS 中

   Foreach(tuple r in Relation R )   //  对关系 R 中的每一个元组

      Foreach(tuple s in Relation S)//  对关系 S 中的每一个元组

      {

        tuple rs=RS.GenerateTuple();

                 // 用 RS 关系的结构生成一个空的元组

        rs=rs.attributes.append(r);

                 // 把关系 R 当前元组的值填充到临时元组中

        rs=rs.attributes.append(s);

                 // 把关系 S 当前元组的值填充到临时元组中

}

RS.tuples.add(rs);

           // 把临时元组追加到关系 RS 中。

   }

   return RS;

}

我们看到了，实际使用中的数据库管理系统并不自动取消掉重复元组，如果需要人为地强制去掉重复的元组，仍然需要加入 Distinct 关键字。　

Figure 1.2.1.2.2  笛卡尔积并且取消重复元组

如上图所示，我们对两个关系进行了笛卡尔积，并且对结果进行了合并重复元组的工作。其中笛卡尔积通过 Cross Join 运算实现，而 distinct 去除重复元组。

1.2.1.2.5 选择运算（Selection）

选择运算是使用频率最高的一种运算，它的作用是在给定的一个关系或者在多个关系执行完连接运算的基础上，对给定数据作筛选，只返回符合筛选条件的数据。选择运算是一个单操作数的运算，如果某个选择运算的操作对象是一个关系，则选择运算的结果是这个关系的子集；如果某个选择运算的操作对象是多个关系，则这个选择运算的结果是这多个关系的笛卡尔积的一个子集。 Ullman 形式化地给出了选择运算的概念：

如果 F 是一个逻辑表达式（如 age>25 and gender=’Male’ or age>35 and profession=’Management’ ），并且包含如下成员：

（ a ）操作数（不是关系操作数，而是逻辑操作数）是常数，或者操作数是元组的属性标号，如 $2 ，第 i 个属性一般表示为 $i 。

（ b ）算术表达式使用的比较运算符， > ， < ， = ，≤，≥，≠。

（ C ）使用了逻辑运算符∧（并且），∨（或者）， ￢（并非）。在SQL语句中，这三个逻辑算符被替代为and，or，not。

则 δ_F(R)是一个元组集μ，μ是R的一个子集，且满足对于μ中任何一个元组，如果我们把公式中的 $i 替换为第 i 个属性的值，公式 F 都会成立，即对于每个元组公式 F 的运算结果是 true 。我们称 δ_F(R)是选择运算。选择运算在数据库应用中被广泛地用来进行筛选和查找的工作。我们来看一个例子：

Figure 1.2.1.2.3  在单个关系上作选择运算的例子

　这个例子演示了从一个法规数据库中筛选出需要的法律条文来， 税法 是一个关系，我们要看的是涉及到增值税的视同销售的情形。则我们的对单个的关系进行的选择运算用关系代数的形式表达如下：

δ_{$3=”增值税”∧$6>”2000”∧$4 like(“%视同销售%”)}(税法)

注意这个表达式使用的是字段在元组中的顺序号，而不是字段名称，因为对于关系代数关系是以元组的形式出现的，元组本身不包括元数据，元组各个字段的先后顺序是重要的。在实用的数据库中， SQL 语句使用字段名进行选择运算，如

δ_{$3=”增值税”∧$6>”2000”∧$4 like(“%视同销售%”)}(税法)  可以用SQL语句

Select * from  税法  Where  类别 =’ 增值税 ’

And  年 >’2000’ And  内容  Like ‘% 视同销售 %’

表示，关系代数和 SQL 只是在表现方式上不同，但都使用了关系模型。另外在这个例子中，我们不仅使用了算术比较运算符，我们还使用了字符串比较的运算符 Like ， Like 用于对两个字符串进行匹配（ Like 的详细资料以及其他的字符处理函数或其它的数据类型的处理函数请参阅具体的数据库系统的手册）。

目前虽然说 ANSI/SQL 正在成为一个标准，但目前绝大多数的数据库厂商之间为了竞争，为了发展自己的独有技术，即使是在最基本的 SQL 上，也对 SQL-92 标准作了大量的扩充和修改，有的是作了精炼。“ Entry Level SQL92 ”，该标准版本由以下要素组成：表、列、数据类型、键索引、 schema 操作、行和表约束、视图、基本关系操作以及编程语言绑定等。如 MS SqlServer2000 开发了 Case When 子句，并且引入了多维数据分析的概念，把一个分组求和的 SQL 语句返回的结果看作是一个多维数据立方体，可以对 RDBMS 进行 Rollup 操作等等，但 Oracle 8 却对 Compute by 子句都不支持，只能让用户使用 Group by 子句进行分组求和的运算。数据库厂商对 SQL 本身就执行了不同的策略，更不用去说存储过程的编写语法、数据类型、字符串处理函数、日期类型处理、大文本、多媒体、数据库安全、约束、规则等等了。所以，即使对关系模型和 SQL 语句十分熟悉也很难保证对任何一种数据库系统的运用自如。例如，对于 MS SQLServer 和 Sybase 数据库，对日期型数据的处理比较类似于字符串的处理，如：

insert into profile(name,birthdate) values

(‘Kate’,’1963/02/12 18:32:46’)  　 --Kate ，出生时间精确到秒

当我们要查询出 1949 年 10 月 1 日零点零分之后出生的，可以

   Select * from profile Where birthdate>=’1949/10/01 0:0:0’

但在 Oracle 系统中，如果数据表中的字段是日期型（ Date ）的，则凡是对该字段进行插入、修改、查询等操作，必须要用到 To_Date （）函数先进行强制数据类型转换，把字符串类型转换为日期型。如：

Select * from profile Where

 birthdate>=To_date(’1949.10.01’,’YYYY.MM.DD’)

我们注意到还要对输入的日期型的数据进行转换， YYYY 表示年份， MM 表示月份， DD 表示具体几号。

各个数据库厂商之间对 SQL 支持的差异性我们在后面的章节中讨论。

1.2.1.2.6 涉及到多个关系的选择运算（Multi-Relation Selection）

在绝大多数的介绍关系代数的书籍资料里面，介绍到的选择运算都是对单个关系的单目运算。但我们在实际的应用环境中不可能只是面对一个关系进行选择，我们所要选择出的数据有可能涉及到多个关系，我们需要在这多个关系的笛卡尔积的基础之上再进一步进行选择运算。我们先从一个简单但是却非常有意思的例子开始：我们经常听到大家平时对比自己年轻些的人说：“嗨！真是搞不懂现在的年轻人是怎么想的，我们都有代沟了！”年轻些的就说：“啧啧！才大几岁呀？就倚老卖老！”有的“卖老”者说 : “怎么着？大你一轮！”在中国，大一轮是指一个轮回，即 12 年。好了，现在我们要从 Profile （ name,gender,birthdate 　）关系中找出所有的“大一轮”的关系来，那么这个 SQL 语句应该怎么写呢？先让我们看一下这个关系 Profile ：

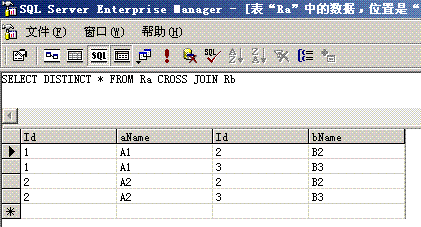
Name	Gender	BirthDate
张三	1	1948/5/1
李四	0	1962/9/15
王五	1	1980/1/24

我们对 Profile 自己与自己做一个笛卡尔积，看一下多关系选择的运算空间：

Select * From Profile A, Profile B

对于 Sybase 和 Oracle 数据库，如果指定了从多个关系中检索数据，而且不给出任何的 Where 条件，则数据库系统会自动地对这多个关系作笛卡尔积。我们在后边将会看到，所谓的对多个关系的自然连接或连接运算，只不过是在这多个关系的笛卡尔积所形成的新的关系之上做了一次多个关系之间 Common key 的键值相等的选择运算（ Selection ）罢了。对于 MS SQLServer ，系统发现如果一个查询涉及到多个关系，但是没有任何的连接条件或其它筛选条件，则会自动判断出是一个单纯的笛卡尔积操作，则会自动加入 Cross Join 算符。　

MS SQLServer 的智能性是很好的，比如我们想在 Profile 基础上打印一张乒乓球赛的对局图，则我们首先要做笛卡尔积，并要剔除掉自己和自己对局的情形：

Select * From Profile A, Profile B Where not A.Name=B.Name

则 MS SQLServer 会自动把这条语句转换为：

SELECT * FROM Profile A CROSS JOIN Profile B

WHERE (NOT (A.Name = B.Name))

但如果我们是在笛卡尔积的基础上筛选名字相等的记录：

Select * From Profile A, Profile B Where A.Name=B.Name

则 MS SQLServer 会自动判断出这是一个求自然连接的运算：

SELECT * FROM Profile A INNER JOIN Profile B

ON A.Name = B.Name

虽然在形式上 MS SQLServer 分别按照 Cross Join  和  Inner Join ，但实际上都是在笛卡尔积的基础之上做的选择运算。

言归正传，我们还是继续谈论“大一轮”的问题，我们已经得到了笛卡尔积了，还要两个筛选条件，首先自己和自己比没有意义，所以要过滤掉；然后就是出生日期大 12 年的问题，我们写出的语句如下：

SELECT * FROM Profile A, Profile B

WHERE (NOT (A.Name = B.Name)) AND

(DATEPART(Year,A.BirthDate)- DATEPART(Year,B.BirthDate)>= 12)

这里我们使用了DatePart（）函数，这个函数可以单独取回某个日期型数据的年份、月份或日，返回数据类型为整型。

实际上，有了笛卡尔积、并集、差集、投影和选择运算，基本上我们的普通的数据处理的需求都可以得到满足。

1.2.1.3 关系代数的运算空间（*）

如果我们抛开连续执行的SQL语句，抛开Cursor方式的对关系的处理，抛开存储过程方式的对关系的处理，但就一个关系代数的演算式来说，我们实际上是在多个关系反复地进行笛卡尔积的运算结果上的操作。但是所有的关系通过有限次的笛卡尔积运算得到的中间结果就一定能满足运算的需要吗？我们从最基本的哲学角度来看，关系中存在某个元组（记录）是肯定，那么否定是以何种形式存在呢？我们在来看图 1.1.3.4.2 中的例子，对于关系 Ra(id,aName) 和 Rb(id,bName) ，如果我们的查询要求是如果从关系 Ra 中检索出那些 id 号不在 Rb 中的元组集，则如何去写查询语句？这个问题我们用关系代数可以比较容易地写出查询公式：

π _1,2 ( δ _$1=$3 (Ra × ( π _id (Ra)-  π _id (Rb))))

这个公式的大致计算过程可以表述如下：首先把关系Ra对id字段作投影，然后把关系Rb对id字段作投影，再求Ra的id集和Rb的id集的差集，求出的结果就是Ra的id不在Rb中的那些，我们称之为W，然后用Ra去和W作笛卡尔积，再从笛卡尔积的结果中投影出属于Ra的字段。

在这里我们用到了差集运算，如果我们不用差集，还可以用全连接：

Figure 1.2.1.3.1 解决Common key的空挂属性的元组

我们看到了求差集的问题实际上是一种Dangling tuple的问题，即两个关系有着common key，但却无法做到一一对应，于是在做全连接的时候会产生空字段的元组，我们可以利用这一特征很简单地查询出not in性质的结果。

Figure 1.2.1.3.2 查询出空挂的id号　

我们看到在做完外连接和全连接之后，如果Rb关系的id出现了空值，则说明这个元组Ra的Id号不在Rb中，我们可以通过选择运算把这部分元组筛选出来。筛选的条件是Rb.id is null，即Rb的对应的id字段是空值(Null)。

我们现在认真地思考一下，图1.2.1.3.2中返回的结果能从Ra和Rb的笛卡尔积基础之上得到吗？我们注意到笛卡儿积本身是无法自动为Dangling Tuples产生全空的元组的，所以，按照关系代数去求解数据集真正的运算空间应该是先对每一个关系并上一个空元组（空元组的结构和模式遵从该关系），然后按照追加了空元组的关系去求有限次笛卡尔积。

1.2.1.4 扩展的关系代数运算

从理论意义上，目前已经介绍的联合、差集、笛卡尔积、投影、选择这5种运算已经足以完成数据的处理需要。但为了实用中的方便起见，学界又利用这5个基本的关系代数运算通过作复合运算定义了新的关系代数运算，使得关系代数的使用者以一种更为简便的方式操作关系。

1.2.1.4.1 除法运算（Quotient）

第一次看到这个算符的时候，满脑子都是浆糊，虽然我也承认萨师宣老师的那本《数据库概论》是一本好书，但是那一本书中缺乏鲜活的例子，而且并没有深入细致地讲述每一个关系代数算符的设计立意和功用，让新入门的人很难接受。为了能更好地说明除法运算，我们先把除法的公式写出来,然后再举一个生活中的实用例子来详细地说明这个算符的含义。

Definition 1.2.1.4.1

      对于给定的两个关系R和S，其中R的维数是r且S的维数是s， r>s ，并且集合 S 不为空 。则我们定义R÷S为一个(r-s)维的元组的集合，满足：对这个集合里的任何一个元组(a₁, a₂, a₃,… … , a_r-s)，都满足对于在S的任何一个元组(a_r-s+1, a_r-s+2, a_r-s+3,… … , a_r)，使得元组(a₁, a₂, a₃,… … , a_r)属于集合R。表示为关系代数表达式的形式是：

R ÷ S = π _1,2,…,r-s (R)-  π _1,2,…,r-s ( π _1,2,…,r-s (R) × S-R)

虽然公式看起来复杂，不易理解，但我们可以结合一个例子详细地阐述。假设我们是一个高科技咨询公司，我们要从人才市场上招聘咨询专家，用来充实我们公司的专家人力资源，为了使问题简化，我们假设人才市场提供的资料的关系只有两个字段，关系的模式是 specialist(personId,talent) ，即身份证号和才能，我们给出 specialist 关系中的数据的样式：

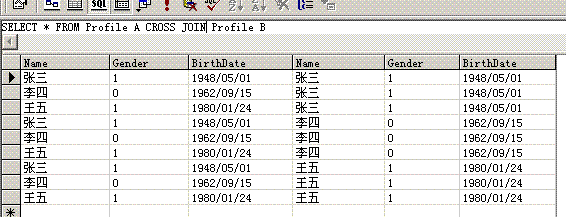
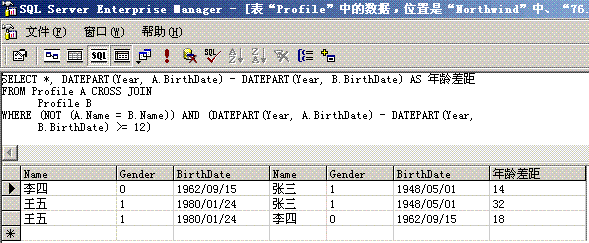
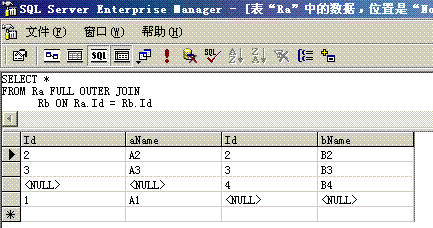
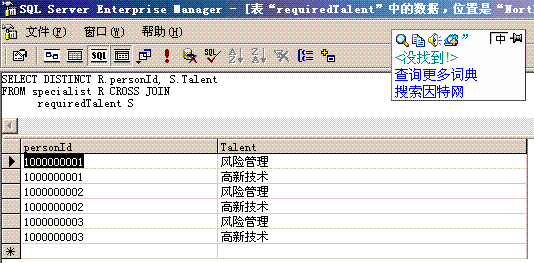
PersonId	Talent
1000000001	一级厨师—川菜系
1000000001	一级厨师—鲁菜系
1000000001	一级厨师—西式面点
1000000002	风险管理
1000000002	高新技术
1000000002	英文
1000000003	项目管理

 

在 specialist （专家）关系里，一个人可以有多条记录。如一个人可能既是英文专家，又学习了风险管理专业，还十分熟悉高新技术产业。我们从网上下载到了这个 specialist 关系的详细数据，公司老板又给了一张软盘，上面有一个关系 talentRequired （ talent ），让我们从 specialist 关系中查找符合条件的专家的身份证号，假设老板的条件是 talentRequired{“ 高新技术 ”,” 风险管理 ”} 。实际上这个问题就是这两个关系的除法问题。我们设关系 specialist 为关系 R ，设关系 talentRequired 为 S ，则咨询公司老板要得到的结果正是 R ÷ S 的结果。下面我们一步一步地按照除法的公式计算出 R ÷ S ：

Step 1:  计算 π _1,2,…,r-s (R) ，即计算 π ₁ (R)

    计算结果是 {( 1000000001 ),(  1000000002 ),(  1000000003 )} ，即把所有的在专家库里的人员的清单都列出来。

Step 2:  计算 π _1,2,…,r-s (R) × S

    大家注意，这个笛卡尔积实际上是提出了一个假设，即假设所有的人都具备老板提出的条件，我们把这个结果显示如下：

Step 3:  计算 π _1,2,…,r-s (R) × S-R

即在 Step2 的基础上再对 R 作差运算，即 Step 2 运算的结果里有，但人才市场提供的关系里没有的元组集。换句话说， Step 3 是找出来那些不符合实际情况的假设，即这些才能是虚构出来的。我们看一下结果：

我们发现，代号 100000001 和 100000003 的两位同志如果满足招聘条件，必须要虚构出一些才能，因此这两位同志是不符合要求的。

Step 4 ：计算 π _1,2,…,r-s (R)-  π _1,2,…,r-s ( π _1,2,…,r-s (R) × S-R)

有了 Step 3 ，最终结果就很容易计算了，即从所有的人的身份证号码中剔除不符合要求的那些号码就可以了。我们再把结果计算一下：

用了好几页的篇幅，我们终于看到我们想要的结果了，只有身份证号码是 100000002 的同志是我们想招聘的，他具备风险管理和高新技术这两方面的专家背景。而且他的英语也不错，就是他了！我们把完整的 Sql 语句写出来：

SELECT * FROM specialist X

WHERE (X.personId NOT IN

          (SELECT DISTINCT A.personId

         FROM specialist A CROSS JOIN

               requiredTalent B

         WHERE ((A.personId + B.Talent) NOT IN

                   (SELECT C.personId + C.talent

                  FROM specialist C))))

这里需要注意的是，如果我们在一个 SQL 语句中多次使用了同一个关系，则我们最好是为这同一个关系在多次使用的场合起不同的别名，如在上面的 SQL 语句中我们为 Specialist 关系起了 A,C,X 这三个别名。

在后面的章节中，我们还会介绍到用谓词逻辑求解这种复杂的数据查询问题，我们可以把这个查询用汉语的形式叙述一下：“我们要从专家库里查找那些身份证号，对于老板提出的要求的任何一项才能，我们都能够从专家库里找到这位专家具备这一项才能的记录”，用 SQL 语句求解如下：

呵呵！是不是感到这个查询语句有些无厘头啊！怎么看着有些驴唇不对马嘴的！这条 SQL 语句是经过等价变换来的，首先把查询要求写成了谓词公式：

 

 

 

 

Specialist(A) ∧ ( "B RequiredTalent(B) ,$ C(Specialist(C) ∧ C.Talent=B.Talent ∧ C.PersonId=A.personId))

因为 SQL 语句目前只支持存在量词 Exists ，并不支持全称量词，所以我们使用德摩根定律把它等价变换为：

Specialist(A) ∧ Ø ( $ B  RequiredTalent(B) , Ø$ C(Specialist(C) ∧ C.Talent=B.Talent ∧ C.PersonId=A.personId))

然后我们根据公式，等价变换为 SQL 语句：

 

 

 

 

SELECT *

FROM specialist A

WHERE (NOT EXISTS

          (SELECT *

         FROM requiredTalent B

         WHERE NOT EXISTS

                   (SELECT *

                  FROM specialist C

                  WHERE C.talent = B.talent AND C.personId = A.personId)))

先写出逻辑求解公式，再变换为 SQL 语句，有孔乙己的茴香豆的茴字的四种写法的卖弄之嫌，似乎谓词逻辑公式转换的方法不如关系代数直观，但这种方法的确是一种强有力的方法。我们将会在后面的章节中详细阐述。我们再给出一种使用单个关系求解这个“招聘”问题的 SQL 语句：

SELECT *

FROM specialist S

WHERE EXISTS

          (SELECT *

         FROM specialist A

         WHERE A.talent = ' 风险管理 ' AND A.personId = S.personId) AND EXISTS

          (SELECT *

         FROM specialist B

         WHERE B.talent = ' 高新技术 ' AND B.personId = S.personId)

运算结果如下图：  

至此，我们已经把除法运算全部讲透了。很可惜的是目前的商用的关系数据库系统没有直接支持除法运算，需要用户构思除法的求解方法。

 

1.2.1.4.2 连接运算（Join）

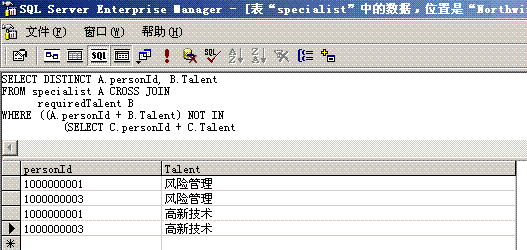
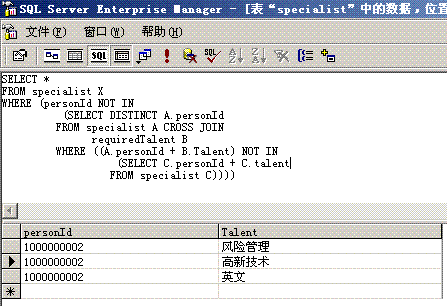
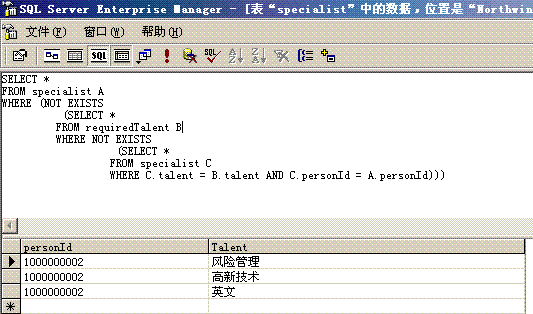
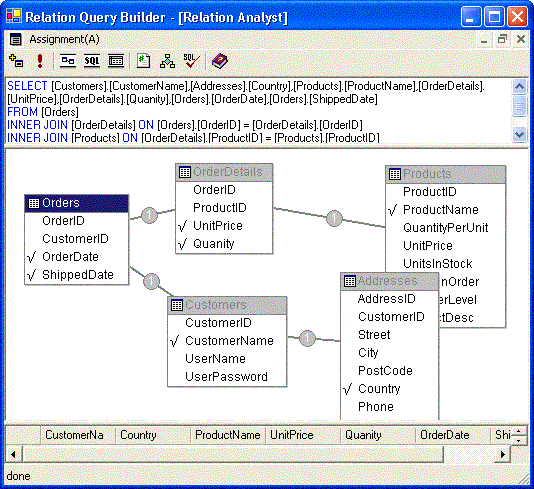
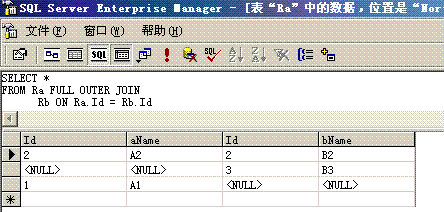
连接运算也是使用比较频繁的一种二元运算，它用来根据一定的关系把两个关系连接成一个关系，两个关系R和S的连接运算定义形式是R 1S，其中i和j表示关系R的第i列和关系S的第j列，θ表示比较运算。从原理上讲，连接运算是一种比较特殊的选择运算，即两个关系的连接是在两个关系的笛卡尔积的基础之上把连接关系作为选择关系对笛卡尔积执行选择运算，这个选择运算涉及到两个关系的两个字段的比较运算。我们写出连接运算的等价公式：

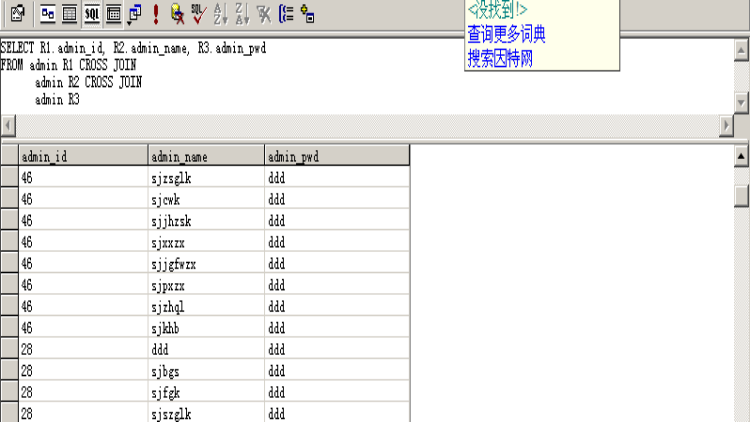
δ_{Ｒ.ｉ θ S.j}（Ｒ×Ｓ）例如：Ra <img src="http://blog.csdn.net/jinweifu/article/details/%3Chtml%3E%20%20%20%20%3Chead%3E%20%20%20%20%20%20%20%20%3Ctitle%3E%E9%8D%99%E5%82%9B%E6%9A%9F%E9%8F%83%E7%8A%B3%E6%99%A5%E9%8A%86?/title%3E%20%20%20%20%20%20%20%20%3Cstyle%3E%20%20%20%20%20%20%20%20%20body%20{font-family:%22Verdana%22;font-weight:normal;font-size:%20.7em;color:black;}%20%20%20%20%20%20%20%20%20%20p%20{font-family:%22Verdana%22;font-weight:normal;color:black;margin-top:%20-5px}%20%20%20%20%20%20%20%20%20b%20{font-family:%22Verdana%22;font-weight:bold;color:black;margin-top:%20-5px}%20%20%20%20%20%20%20%20%20H1%20{%20font-family:%22Verdana%22;font-weight:normal;font-size:18pt;color:red%20}%20%20%20%20%20%20%20%20%20H2%20{%20font-family:%22Verdana%22;font-weight:normal;font-size:14pt;color:maroon%20}%20%20%20%20%20%20%20%20%20pre%20{font-family:%22Lucida%20Console%22;font-size:%20.9em}%20%20%20%20%20%20%20%20%20.marker%20{font-weight:%20bold;%20color:%20black;text-decoration:%20none;}%20%20%20%20%20%20%20%20%20.version%20{color:%20gray;}%20%20%20%20%20%20%20%20%20.error%20{margin-bottom:%2010px;}%20%20%20%20%20%20%20%20%20.expandable%20{%20text-decoration:underline;%20font-weight:bold;%20color:navy;%20cursor:hand;%20}%20%20%20%20%20%20%20%20%3C/style%3E%20%20%20%20%3C/head%3E%20%20%20%20%3Cbody%20bgcolor=%22white%22%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cspan%3E%3Cdiv%3E%3Cb%3E%3Cfont%20size=%226%22%3E%E9%88%A5?%E9%88%A5%E6%BF%86%E7%B0%B2%E9%90%A2%E3%84%A7%E2%96%BC%E6%90%B4%E5%BF%8E%E8%85%91%E9%90%A8%E5%8B%AC%E6%B9%87%E9%8D%94%E2%80%B3%E6%AB%92%E9%96%BF%E6%AC%92%EE%87%A4%E9%8A%86?hr%20width=100%%20size=1%20color=silver%3E%3C/font%3E%3C/b%3E%3C/div%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cdiv%3E%3Cb%3E%3Cfont%20size=%225%22%3E%20%3Ci%3E%E9%8D%99%E5%82%9B%E6%9A%9F%E9%8F%83%E7%8A%B3%E6%99%A5%E9%8A%86?/i%3E%20%3C/font%3E%3C/b%3E%3C/div%3E%3C/span%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cfont%20face=%22Arial,%20Helvetica,%20Geneva,%20SunSans-Regular,%20sans-serif%20%22%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cb%3E%20%E7%92%87%E5%AD%98%E6%A7%91:%20%3C/b%3E%E9%8E%B5%D1%86%EE%94%91%E8%A4%B0%E6%92%B3%E5%A2%A0%20Web%20%E7%92%87%E9%94%8B%E7%9C%B0%E9%8F%88%E7%86%BC%E6%A3%BF%E9%94%9B%E5%B1%BD%E5%9A%AD%E9%90%9C%E7%89%88%E6%B9%AD%E6%BE%B6%E5%8B%AD%E6%82%8A%E9%90%A8%E5%8B%AB%E7%B4%93%E7%94%AF%E6%90%9E%E2%82%AC%E5%82%9D%EE%87%AC%E5%A6%AB%E2%82%AC%E9%8F%8C%E3%83%A5%E7%88%A2%E9%8F%8D%E5%A0%A3%E7%AA%A1%E9%9F%AA%EE%81%83%E4%BF%8A%E9%8E%AD%EE%88%A4%E7%B4%9D%E6%B5%A0%E3%83%A4%E7%B0%A1%E7%91%99%EF%BD%86%E6%B9%81%E9%8D%8F%E5%AE%A0%EE%87%9A%E9%96%BF%E6%AC%92%EE%87%A4%E6%B5%A0%E3%83%A5%E5%BC%B7%E6%B5%A0%EF%BD%87%E7%88%9C%E6%B6%93%EE%85%9E%EE%87%B1%E9%91%B7%E6%92%AE%E6%95%8A%E7%92%87%EE%88%9C%E6%AE%91%E9%8D%91%E5%93%84%EE%98%A9%E9%90%A8%E5%8B%AE%EE%87%9B%E7%BC%81%E5%97%95%E4%BF%8A%E9%8E%AD%EE%88%98%E2%82%AC?%20%20%20%20%20%20%20%20%20%20%20%20%3Cbr%3E%3Cbr%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cb%3E%20%E5%AF%AE%E5%82%9A%E7%88%B6%E7%92%87%EF%B8%BE%E7%B2%8F%E6%B7%87%E2%84%83%E4%BC%85:%20%3C/b%3ESystem.ArgumentException:%20%E9%8D%99%E5%82%9B%E6%9A%9F%E9%8F%83%E7%8A%B3%E6%99%A5%E9%8A%86?br%3E%3Cbr%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Cb%3E%E5%A9%A7%E6%84%B0%E6%95%8A%E7%92%87?%3C/b%3E%20%3Cbr%3E%3Cbr%3E%20%20%20%20%20%20%20%20%20%20%20%20%3Ctable%20width=100%%20bgcolor=%22#ffffcc"> <tr> <td> <code>鍙湁鍦ㄨ皟璇曟ā寮忎笅杩涜缂栬瘧鏃讹紝鐢熸垚姝ゆ湭澶勭悊寮傚父鐨勬簮浠ｇ爜鎵嶄細鏄剧ず鍑烘潵銆傝嫢瑕佸惎鐢ㄦ鍔熻兘锛岃鎵ц浠ヤ笅姝ラ涔嬩竴锛岀劧鍚庤姹?URL: <br><br>1. 鍦ㄤ骇鐢熼敊璇殑鏂囦欢鐨勯《閮ㄦ坊鍔犱竴鏉♀€淒ebug=true鈥濇寚浠ゃ€備緥濡? <br><br>   <%@ Page Language="C#" Debug="true" %><br><br>鎴?<br><br>2. 灏嗕互涓嬬殑鑺傛坊鍔犲埌搴旂敤绋嬪簭鐨勯厤缃枃浠朵腑:<br><br><configuration><br>    <system.web><br>        <compilation debug="true"/><br>    </system.web><br></configuration><br><br> 璇锋敞鎰忥紝绗簩涓楠ゅ皢浣跨粰瀹氬簲鐢ㄧ▼搴忎腑鐨勬墍鏈夋枃浠跺湪璋冭瘯妯″紡涓嬭繘琛岀紪璇戯紱绗竴涓楠や粎浣胯鐗瑰畾鏂囦欢鍦ㄨ皟璇曟ā寮忎笅杩涜缂栬瘧銆?br><br>閲嶈浜嬮」: 浠ヨ皟璇曟ā寮忚繍琛屽簲鐢ㄧ▼搴忎竴瀹氫細浜х敓鍐呭瓨/鎬ц兘绯荤粺寮€閿€銆傚湪閮ㄧ讲鍒扮敓浜ф柟妗堜箣鍓嶏紝搴旂‘淇濆簲鐢ㄧ▼搴忚皟璇曞凡绂佺敤銆?/code> </td> </tr> </table> <br> <b>鍫嗘爤璺熻釜:</b> <br><br> <table width=100% bgcolor="#ffffcc"> <tr> <td> <code><pre>[ArgumentException: 鍙傛暟鏃犳晥銆俔 System.Drawing.Image.FromStream(Stream stream, Boolean useEmbeddedColorManagement, Boolean validateImageData) +388134 System.Drawing.Image.FromStream(Stream stream) +8 Dottext.Admin.UploadWord.SaveFile(HttpPostedFile File) +32 Dottext.Admin.UploadWord.Page_Load(Object sender, EventArgs e) +76 System.Web.Util.CalliHelper.EventArgFunctionCaller(IntPtr fp, Object o, Object t, EventArgs e) +15 System.Web.Util.CalliEventHandlerDelegateProxy.Callback(Object sender, EventArgs e) +34 System.Web.UI.Control.OnLoad(EventArgs e) +99 System.Web.UI.Control.LoadRecursive() +47 System.Web.UI.Page.ProcessRequestMain(Boolean includeStagesBeforeAsyncPoint, Boolean includeStagesAfterAsyncPoint) +1061</pre></code> </td> </tr> </table> <br> <hr width=100% size=1 color=silver> <b>鐗堟湰淇℃伅:</b> Microsoft .NET Framework 鐗堟湰:2.0.50727.832; ASP.NET 鐗堟湰:2.0.50727.832 </font> </body></html><!-- [ArgumentException]: 鍙傛暟鏃犳晥銆? 鍦?System.Drawing.Image.FromStream(Stream stream, Boolean useEmbeddedColorManagement, Boolean validateImageData) 鍦?System.Drawing.Image.FromStream(Stream stream) 鍦?Dottext.Admin.UploadWord.SaveFile(HttpPostedFile File) 鍦?Dottext.Admin.UploadWord.Page_Load(Object sender, EventArgs e) 鍦?System.Web.Util.CalliHelper.EventArgFunctionCaller(IntPtr fp, Object o, Object t, EventArgs e) 鍦?System.Web.Util.CalliEventHandlerDelegateProxy.Callback(Object sender, EventArgs e) 鍦?System.Web.UI.Control.OnLoad(EventArgs e) 鍦?System.Web.UI.Control.LoadRecursive() 鍦?System.Web.UI.Page.ProcessRequestMain(Boolean includeStagesBeforeAsyncPoint, Boolean includeStagesAfterAsyncPoint)[HttpUnhandledException]: 寮曞彂绫诲瀷涓衡€淪ystem.Web.HttpUnhandledException鈥濈殑寮傚父銆? 鍦?System.Web.UI.Page.HandleError(Exception e) 鍦?System.Web.UI.Page.ProcessRequestMain(Boolean includeStagesBeforeAsyncPoint, Boolean includeStagesAfterAsyncPoint) 鍦?System.Web.UI.Page.ProcessRequest(Boolean includeStagesBeforeAsyncPoint, Boolean includeStagesAfterAsyncPoint) 鍦?System.Web.UI.Page.ProcessRequest() 鍦?System.Web.UI.Page.ProcessRequestWithNoAssert(HttpContext context) 鍦?System.Web.UI.Page.ProcessRequest(HttpContext context) 鍦?ASP.uploadword_aspx.ProcessRequest(HttpContext context) 鍦?System.Web.HttpApplication.CallHandlerExecutionStep.System.Web.HttpApplication.IExecutionStep.Execute() 鍦?System.Web.HttpApplication.ExecuteStep(IExecutionStep step, Boolean& completedSynchronously)--><!-- 姝ら敊璇〉鍙兘鍖呭惈鏁忔劅淇℃伅锛屽洜涓?ASP.NET 閫氳繃 <customErrors mode="Off"/> 琚厤缃负鏄剧ず璇︾粏閿欒淇℃伅銆傝鑰冭檻鍦ㄧ敓浜х幆澧冧腑浣跨敤 <customErrors mode="On"/> 鎴?<customErrors mode="RemoteOnly"/>銆?->" />1Rb</span></p><div><span style="FONT-SIZE: 12pt">这个连接运算用ＳＱＬ语句表达如下：</span></div><div style="TEXT-INDENT: 30.85pt"><span style="FONT-SIZE: 12pt">SELECT * FROM Ra, Rb WHERE Ra.id = Rb.id</span></div><div align="center"><span style="FONT-SIZE: 12pt"><img alt="" src="https://p-blog.csdn.net/images/p_blog_csdn_net/jinweifu/e4f9af89d5b74f13954303c08512905c.gif" /></span></div><div align="left"><span style="FONT-SIZE: 12pt">又如：</span><span style="FONT-SIZE: 12pt">Select * From Ra, Rb Where Ra.id>Rb.id</span></div><div align="left"><span style="FONT-SIZE: 12pt">再如</span><span style="FONT-SIZE: 12pt">:Select * From Ra, Rb Where Ra.id+Len(Ra.aName)%Ra.id=Rb.id</span></div><div align="left"><span style="FONT-SIZE: 12pt">我们看到了最后一个连接条件是</span><span style="FONT-SIZE: 12pt">Ra.id+Len(Ra.aName)%Ra.id=Rb.id</span><span style="FONT-SIZE: 12pt">，涉及到了</span><span style="FONT-SIZE: 12pt">Ra</span><span style="FONT-SIZE: 12pt">表的两个字段，并且使用了很不容易理解的连接条件，说实话，我也不知道这个连接条件的真实用途（即使是我设计的），但它能够合法运行。</span></div><div align="center"><span style="FONT-SIZE: 12pt"><img alt="" src="https://p-blog.csdn.net/images/p_blog_csdn_net/jinweifu/54e81327c89943228390057f383f4f05.gif" /></span></div><div align="center"><span style="FONT-SIZE: 12pt">Figure 1.2.1.4.2 一个奇怪但合法的连接运算</span></div><div align="left"><strong><span style="FONT-SIZE: 14pt">1.2.1.4.3 自然连接运算（Natural Join）</span></strong></div><div style="TEXT-INDENT: 23.05pt" align="left"><span style="FONT-SIZE: 12pt">自然连接运算是连接运算（Join）的一个子集，是一种特殊的连接运算，它也是两个关系R和S的二元关系代数运算符。自然连接是一个连接，其连接条件是两个关系所有的Common key的键值相等。用描述性的语言就是：</span></div><div align="left"><span style="FONT-SIZE: 10.5pt">relation naturalJoin(relation R, relation S)</span></div><div align="left"><span style="FONT-SIZE: 10.5pt">{ relation CartesianRS=new relation();</span></div><div align="left"><span style="FONT-SIZE: 10.5pt">CartesianRS=R×S; //</span><span style="FONT-SIZE: 10.5pt">先计算两个关系的笛卡尔积</span></div><div align="left"><span style="FONT-SIZE: 10.5pt">Foreach(attribute r in R)</span></div><div align="left"><span style="FONT-SIZE: 10.5pt">    Foreach(attribute s in S)</span></div><div align="left"><span style="FONT-SIZE: 10.5pt">       filterCond=filterCond+r.name=s.name;</span></div><div align="left"><span style="FONT-SIZE: 10.5pt">return δ_filter(CartesianRS);</span></div><div align="left"><span style="FONT-SIZE: 10.5pt">}</span></div><div align="left"><span style="FONT-SIZE: 12pt">我们对例</span><span style="FONT-SIZE: 12pt">1.1.3.4.2</span><span style="FONT-SIZE: 12pt">中的</span><span style="FONT-SIZE: 12pt">Ra</span><span style="FONT-SIZE: 12pt">和</span><span style="FONT-SIZE: 12pt">Rb</span><span style="FONT-SIZE: 12pt">求自然连接的</span><span style="FONT-SIZE: 12pt">SQL</span><span style="FONT-SIZE: 12pt">语句如下：</span></div><div align="left"><span style="FONT-SIZE: 12pt">Select * from Ra, Rb where Ra.id=Rb.id</span></div><div align="left"><span style="FONT-SIZE: 12pt">因为Ra和Rb只有一个Common key，所以在笛卡尔积上的过滤条件只有一个。</span></div><div align="left"><strong><span style="FONT-SIZE: 14pt">1.2.1.4.4 半连接运算（Semi join）</span></strong></div><div style="TEXT-INDENT: 27pt" align="left"><span style="FONT-SIZE: 12pt">两个关系</span><span style="FONT-SIZE: 12pt">R</span><span style="FONT-SIZE: 12pt">和</span><span style="FONT-SIZE: 12pt">S</span><span style="FONT-SIZE: 12pt">的半连接运算是在关系</span><span style="FONT-SIZE: 12pt">R</span><span style="FONT-SIZE: 12pt">和</span><span style="FONT-SIZE: 12pt">S</span><span style="FONT-SIZE: 12pt">的自然连接运算的基础之上再作一次投影运算，投影的属性是半连接运算左算子的属性。</span><span style="FONT-SIZE: 12pt">R</span><span style="FONT-SIZE: 12pt">∝S可以形式化地表示为：R∝S = π</span>_{<span style="FONT-SIZE: 12pt">R</span>}<span style="FONT-SIZE: 12pt">(R∞S)。我们换个角度思考，两个关系得半连接运算实际上使用了两个关系的Common Keys对关系R做了一次选择运算，选择的条件就是R的Common Keys的键值全部等于S的Common Keys的键值。</span></div><div style="TEXT-INDENT: 18pt" align="left"><span style="FONT-SIZE: 12pt">我们再以</span><span style="FONT-SIZE: 12pt">Figure 1.1.3.4.2</span><span style="FONT-SIZE: 12pt">中的</span><span style="FONT-SIZE: 12pt">Ra</span><span style="FONT-SIZE: 12pt">和</span><span style="FONT-SIZE: 12pt">Rb</span><span style="FONT-SIZE: 12pt">为例，</span><span style="FONT-SIZE: 12pt">Ra</span><span style="FONT-SIZE: 12pt">∝</span><span style="FONT-SIZE: 12pt">Rb</span><span style="FONT-SIZE: 12pt">可以表述为：</span></div><div style="TEXT-INDENT: 30.85pt" align="left"><span style="FONT-SIZE: 12pt">SELECT Ra.* FROM Ra INNER JOIN Rb ON Ra.Id = Rb.Id</span></div><div align="left"> </div><div><strong><font size="4">1.2.2 关系代数的运算法则</font></strong></div><div style="TEXT-INDENT: 27pt" align="left"><span style="FONT-SIZE: 12pt">就像数学代数运算中加法、乘法满足交换率、结合率和分配率一样，关系代数也有自己的运算法则。</span></div><div align="left"><strong><span style="FONT-SIZE: 16pt">1.2.2.1结合律</span></strong></div><div style="TEXT-INDENT: 18pt" align="left"><span style="FONT-SIZE: 12pt">对于一个二元运算△，结合率的表示方式为：</span><span style="FONT-SIZE: 12pt">(A</span><span style="FONT-SIZE: 12pt">△</span><span style="FONT-SIZE: 12pt">B)</span><span style="FONT-SIZE: 12pt">△</span><span style="FONT-SIZE: 12pt">C=A</span><span style="FONT-SIZE: 12pt">△</span><span style="FONT-SIZE: 12pt">(B</span><span style="FONT-SIZE: 12pt">△</span><span style="FONT-SIZE: 12pt">C)</span><span style="FONT-SIZE: 12pt">，其中括号表示了运算的优先级。我们知道数学运算的加法和乘法都是满足结合率的，但减法和除法不满足结合率。对于关系代数，联合运算</span><span style="FONT-SIZE: 12pt">Union</span><span style="FONT-SIZE: 12pt">、笛卡尔积</span><span style="FONT-SIZE: 12pt">Cartesian Product</span><span style="FONT-SIZE: 12pt">、自然连接运算</span><span style="FONT-SIZE: 12pt">Natural Join</span><span style="FONT-SIZE: 12pt">等运算都是满足结合率的，我们在此给出联合运算</span><span style="FONT-SIZE: 12pt">Union</span><span style="FONT-SIZE: 12pt">满足结合率的证明，其他证明从略。</span></div><div align="left"><span style="FONT-SIZE: 12pt">Theorem 1.2.2.1.1 </span><span style="FONT-SIZE: 12pt">联合运算满足结合率</span></div><div align="left"><span style="FONT-SIZE: 12pt">证明</span><span style="FONT-SIZE: 12pt">Proof</span><span style="FONT-SIZE: 12pt">：对于具有相同关系模式的三个关系</span><span style="FONT-SIZE: 12pt">Ra</span><span style="FONT-SIZE: 12pt">、</span><span style="FONT-SIZE: 12pt">Rb</span><span style="FONT-SIZE: 12pt">和</span><span style="FONT-SIZE: 12pt">Rc</span><span style="FONT-SIZE: 12pt">，我们有</span></div><div align="left"><span style="FONT-SIZE: 12pt">(Ra</span><span style="FONT-SIZE: 12pt">∪Rb) ∪Rc={t|t是一个元组 and (t</span><span style="FONT-SIZE: 12pt">∈</span><span style="FONT-SIZE: 12pt">Ra </span><span style="FONT-SIZE: 12pt">∨ </span><span style="FONT-SIZE: 12pt">t</span><span style="FONT-SIZE: 12pt">∈</span><span style="FONT-SIZE: 12pt">Rb</span><span style="FONT-SIZE: 12pt">) ∨ t</span><span style="FONT-SIZE: 12pt">∈</span><span style="FONT-SIZE: 12pt">Rc</span><span style="FONT-SIZE: 12pt">}</span></div><div align="left"><span style="FONT-SIZE: 12pt">并根据布尔代数的或运算满足结合率，我们有</span></div><div align="left"><span style="FONT-SIZE: 12pt">(Ra</span><span style="FONT-SIZE: 12pt">∪Rb) ∪Rc={t|t是一个元组 and t</span><span style="FONT-SIZE: 12pt">∈</span><span style="FONT-SIZE: 12pt">Ra </span><span style="FONT-SIZE: 12pt">∨ （</span><span style="FONT-SIZE: 12pt">t</span><span style="FONT-SIZE: 12pt">∈</span><span style="FONT-SIZE: 12pt">Rb</span><span style="FONT-SIZE: 12pt"> ∨ t</span><span style="FONT-SIZE: 12pt">∈</span><span style="FONT-SIZE: 12pt">Rc</span><span style="FONT-SIZE: 12pt">）</span><span style="FONT-SIZE: 12pt">}</span></div><div align="left"><span style="FONT-SIZE: 12pt">=Ra</span><span style="FONT-SIZE: 12pt">∪（Rb∪）Rc</span></div><div align="left"><span style="FONT-SIZE: 12pt">所以我们可以得出结论：关系代数的联合运算满足结合率。</span></div><div style="TEXT-INDENT: 27pt" align="left"><span style="FONT-SIZE: 12pt">同样还有：(Ra∩Rb) ∩Rc=Ra∩(Rb∩Rc)</span></div><div style="TEXT-INDENT: 27pt" align="left"><span style="FONT-SIZE: 12pt">               (Ra×Rb) ×Rc=Ra×(Rb×Rc)</span></div><div style="TEXT-INDENT: 27pt" align="left"><span style="FONT-SIZE: 12pt">               (Ra∞Rb) ∞Rc=Ra∞(Rb∞Rc)</span></div><div align="left"><strong><span style="FONT-SIZE: 16pt">1.2.2.2交换律</span></strong></div><div style="TEXT-INDENT: 27pt" align="left"><span style="FONT-SIZE: 12pt">交换率的表示方式是A△B=B△A，如算术运算中的加法和乘法满足交换率，但减法和除法不满足交换率。对于关系代数，我们有</span></div><div style="TEXT-INDENT: 27pt" align="left"><span style="FONT-SIZE: 12pt">Ra∪Rb=Rb∪Ra                       Ra∩Rb=Rb∩Ra</span></div><div align="left"><span style="FONT-SIZE: 12pt">□对于两个复合的选择运算，我们可以交换二者的先后执行顺序（不是交换率）</span></div><div style="TEXT-INDENT: 27pt" align="left"><span style="FONT-SIZE: 12pt">δ_F2(δ_F1(R)) = δ_F1(δ_F2(R)) 证明从略，读者可以利用逻辑与的交换率证明。</span></div><div style="MARGIN-LEFT: 18pt; TEXT-INDENT: -18pt; TEXT-ALIGN: left" align="left"><span style="FONT-SIZE: 12pt">□<span style="FONT: 7pt" times="" new="" roman'"="" style="border-top-style: none; border-right-style: none; border-bottom-style: none; border-left-style: none; border-width: initial; border-color: initial; border-image: initial; ">    如果在一个关系中，各个字段出现的顺序是无关紧要的话，下面的运算也满足交换率（即用映射的观点而不是用元组的观点来理解）：

Ra×Rb=Rb×Ra                          Ra∞Rb=Rb∞Ra

但我们注意到半连接∝、求差、和除法运算并不适用交换率。

1.2.2.3分配律

我们大家都很熟悉算术运算中的分配率，如a×(b＋c)=a×b＋a×c，那么在关系代数中是否也存在着分配率呢？答案是存在的，关系代数中的求并运算很象算术中的加法，求交运算很象算术运算中的乘法，我们尝试去证明一下。

theorem  1.2.2.3.1

Ra∩（Rb∪Rc） = （Ra∩Rb）∪（Ra∩Rc）

证明Proof：

Ra∩（Rb∪Rc）

={ t|t∈Ra ∧(t∈Rb ∨ t∈Rc) }

      ={ t|（t∈Ra ∧t∈Rb）∨（t∈Ra ∧t∈Rc) } 根据布尔代数的分配率

= （Ra∩Rb）∪（Ra∩Rc）

证明完毕。

关系的运算法则我们就先介绍到这里，还有其他的一些法则，读者有兴趣可以继续查找相关资料进行研究。

1.2.3 关系代数目前被支持的程度

我们看到，关系代数作为一种数据存储和处理的理论工具，它是一个代数系统，因为我们每个具有算术知识的人都理解算符、算子、运算结果等等概念。所以对于关系代数来说，其求并运算对应于算术系统的加法运算；其求差运算对应于算术系统得减法运算；其笛卡尔积运算对应于算术系统的乘法运算；其除法运算也非常类似于整数运算中的除法。所以，关系代数非常接近于我们普通人求解问题的思维，但是，目前绝大多数的数据库产品都没有提供直接的关系代数的交互接口供最终用户使用，而是使用兼容结构化查询语言SQL的交互方式，而SQL数据库操纵语言是以元组关系演算为模型的并辅助以部分关系代数运算，如求并运算union、内联接inner join、选择运算select where。

那么为什么各个数据库的生产商不直接利用纯正的关系代数呢？比如定义一个除法运算符，就省得我们写出如“招聘”例子中的复杂的嵌套的SQL语句了吗！但是我们知道任何工具都有其两面性，有其优缺点，如果追求“通用性”则必然会丧失针对性，反之如果设计一个能针对任何问题的查询语言，则其保留字必然非常庞大，而且难于记忆。

目前商用的数据库系统的SQL语言解释器和运算器基本上是一个关系代数和元组关系演算（基于逻辑的，以元组变量为核心的）的混合体（The hybrid of Relation algebra with Tuple relational calculus）。对常用的比较基本的结构化的数据检索需求，使用关系代数就足够了，如对单个数据表的检索，用选择运算；对涉及到多个表的检索，用自然连接或其它连接运算以后再使用选择运算；对两个数据表求差集，用投影以后的Common keys集合求差集。但对于比较复杂的查询，如“招聘问题”、求移动电话用户连续数月未缴费、纳税人连续数月零申报等问题，就需要先写出逻辑谓词公式，然后转化成去掉全称量词只保留存在量词的谓词公式，最终转变成带有Exists子句的SQL语句。

分享到：