数据库2_3——关系代数
1. 简介
- 关系代数是一种抽象的查询语言,它用对关系的运算来表达查询
- 关系代数
- 运算对象 是 关系
- 运算结果 是 关系
- 关系代数运算有两类:集合运算和专门的关系运算
- 传统的集合运算是从关系的“水平”方向即行的角度进行
- 专门的关系运算不仅涉及行而且涉及列
【这个行与列的区别需要好好斟酌】
运算符

2. 传统的集合运算
传统的集合运算不细讲,并(union)与交(intersection),高中老朋友了,讲一下差(difference)和笛卡尔积(Cartesian Product)吧!
- 差
R - S : 由属于R而不属于S的所有元组组成, R − S = { t ∣ t ∈ R ∩ t ∉ S } R - S = \{ t|t\in R \cap t\notin S \} R−S={t∣t∈R∩t∈/S}
- R,S具有相同的目n
- R,S相应的属性取自同一个域

- 笛卡尔积 (文字不用看,直接看图)
R: n目关系,k1个元组
S: m目关系,k2个元组
R×S
列:(n+m)列元组的集合
(1)元组的前n列是关系R的一个元组
(2)后m列是关系S的一个元组
行:k1×k2个元组

3. 专门的关系运算
记号的引入
-
R , t ∈ R , t [ A i ] R,t\in R,t[Ai] R,t∈R,t[Ai]
(1)设关系模式为R(A1,A2,…,An)
它的一个关系设为R
(2) t ∈ R t\in R t∈R表示t是关系R的一个元组
(3) t [ A i ] t[Ai] t[Ai] 则表示元组t中相应于属性Ai的一个分量 -
A , t [ A ] , A ˉ A,t[A], \bar A A,t[A],Aˉ
(1)若 A = { A i 1 , A i 2 , … , A i k } A=\{Ai1,Ai2,…,Aik\} A={Ai1,Ai2,…,Aik},其中 A i 1 , A i 2 , … , A i k Ai1,Ai2,…,Aik Ai1,Ai2,…,Aik是 A 1 , A 2 , … , A n A1,A2,…,An A1,A2,…,An中的一部分,则A称为属性列或属性组。
(2) t [ A ] = ( t [ A i 1 ] , t [ A i 2 ] , … , t [ A i k ] ) t[A]=(t[Ai1],t[Ai2],…,t[Aik]) t[A]=(t[Ai1],t[Ai2],…,t[Aik])表示元组t在属性列A上诸分量的集合。
(3) A ˉ \bar A Aˉ则表示 { A 1 , A 2 , … , A n } \{A1,A2,…,An\} {A1,A2,…,An}中去掉 { A i 1 , A i 2 , … , A i k } \{Ai1,Ai2,…,Aik\} {Ai1,Ai2,…,Aik}后剩余的属性组。 -
t r t s ⌢ \overset{\frown}{t_{r}t_{s}} trts⌢
R为n目关系,S为m目关系。
t r ∈ R , t s ∈ S , t r t s ⌢ t_{r}\in R,t_{s}\in S,\overset{\frown}{t_{r}t_{s}} tr∈R,ts∈S,trts⌢称为元组的连接。
t r t s ⌢ \overset{\frown}{t_{r}t_{s}} trts⌢是一个 n + m n + m n+m列的元组,前n个分量为R中的一个n元组,后m个分量为S中的一个m元组 -
象集 Z x Z_{x} Zx
给定一个关系R(X,Z),X和Z为属性组。
当t[X]=x时,x在R中的象集(Images Set)为: Z x = { t [ Z ] ∣ t ∈ R , t [ X ] = x } Zx=\{ t[Z]|t \in R,t[X]=x\} Zx={t[Z]∣t∈R,t[X]=x}
它表示R中属性组X上值为x的诸元组在Z上分量的集合

学生关系数据库
学生-课程数据库:学生关系Student、课程关系Course、选修关系SC
- Student

- Course

- SC

3.1 选择
- 选择又称为限制(Restriction)
- 选择运算符的含义
在关系R中选择满足给定条件的诸元组
σ F ( R ) = { t ∣ t ∈ R ∩ F ( t ) = 真 } σ_{F}(R) = \{ t | t\in R\cap F(t)= 真 \} σF(R)={t∣t∈R∩F(t)=真}
F:选择条件,是一个逻辑表达式,取值为“真”或“假”
基本形式为: X 1 θ Y 1 X_{1}θY_{1} X1θY1
θ表示比较运算符,它可以是>,≥,<,≤,=,<> - 选择运算是从关系R中选取使逻辑表达式F为真的元组,是从行的角度进行的运算
- 例子:
σ
C
n
o
=
1
(
S
C
)
σ_{Cno=1}(SC)
σCno=1(SC)

3.2 投影(Projection)
- 从R中选择出若干属性列组成新的关系
π A ( R ) = { t [ A ] ∣ t ∈ R } π_{A}(R) = \{ t[A] | t \in R \} πA(R)={t[A]∣t∈R}
A:R中的属性列 - 投影操作主要是从列的角度进行运算
- 投影之后不仅取消了原关系中的某些列,而且还可能取消某些元组(避免重复行)
- 例子:
π
S
n
a
m
e
,
S
d
e
p
t
(
S
t
u
d
e
n
t
)
π_{Sname,Sdept}(Student)
πSname,Sdept(Student)

3.3 连接(Join)
3.3.1 定义
- 连接也称为θ连接
- 连接运算的含义
从两个关系的笛卡尔积中选取属性间满足一定条件的元组
R ⋈ A θ B S = { t r t s ⌢ ∣ t r ∈ R ∩ t s ∈ S ∩ t r [ A ] θ t s [ B ] } R\mathop{\bowtie}\limits_{AθB} S = \{ \overset{\frown}{t_{r}t_{s}}|t_{r}\in R\cap t_{s} \in S\cap t_{r}[A]θt_{s}[B] \} RAθB⋈S={trts⌢∣tr∈R∩ts∈S∩tr[A]θts[B]}
(1)A和B:分别为R和S上度数相等且可比的属性组
(2)θ:比较运算符 - 连接运算从R和S的广义笛卡尔积R×S中选取R关系在A属性组上的值与S关系在B属性组上的值满足比较关系θ的元组
3.3.2 两种常用的连接运算
- 等值连接(equijoin)
θ为“=”的连接运算称为等值连接
从关系R与S的广义笛卡尔积中选取A、B属性值相等的那些元组,即等值连接为: R ⋈ A = B S = { t r t s ⌢ ∣ t r ∈ R ∩ t s ∈ S ∩ t r [ A ] = t s [ B ] } R\mathop{\bowtie}\limits_{A=B} S = \{ \overset{\frown}{t_{r}t_{s}}|t_{r}\in R\cap t_{s} \in S\cap t_{r}[A]=t_{s}[B] \} RA=B⋈S={trts⌢∣tr∈R∩ts∈S∩tr[A]=ts[B]} - 自然连接(Natural join)
自然连接是一种特殊的等值连接
两个关系中进行比较的分量必须是相同的属性组
在结果中把重复的属性列去掉
自然连接的含义:R和S具有相同的属性组B
R ⋈ S = { t r t s ⌢ [ U − B ] ∣ t r ∈ R ∩ t s ∈ S ∩ t r [ B ] = t s [ B ] } R\mathop{\bowtie} S = \{ \overset{\frown}{t_{r}t_{s}}[U-B]|t_{r}\in R\cap t_{s} \in S\cap t_{r}[B]=t_{s}[B] \} R⋈S={trts⌢[U−B]∣tr∈R∩ts∈S∩tr[B]=ts[B]} - 一般的连接操作是从行的角度进行运算。
自然连接还需要取消重复列,所以是同时从行和列的角度进行运算。
3.3.3 例子

-
一般链接 : R ⋈ C < E S R\mathop{\bowtie}\limits_{C<E} S RC<E⋈S

-
等值连接: R ⋈ R . B = S . B S R\mathop{\bowtie}\limits_{R.B=S.B} S RR.B=S.B⋈S
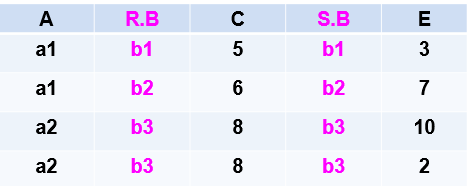
-
自然连接: R ⋈ S R\mathop{\bowtie} S R⋈S

3.3.4 悬浮元祖(Dangling tuple)
两个关系R和S在做自然连接时,关系R中某些元组有可能在S中不存在公共属性上值相等的元组,从而造成R中这些元组在操作时被舍弃了,这些被舍弃的元组称为悬浮元组。
例如:做自然连接时R的第四个元组,S的第五个元组
3.3.5 外连接(Outer Join)
- 如果把悬浮元组也保存在结果关系中,而在其他属性上填空值(Null),就叫做外连接
- 左外连接(LEFT OUTER JOIN或LEFT JOIN):只保留左边关系R中的悬浮元组
- 右外连接(RIGHT OUTER JOIN或RIGHT JOIN):只保留右边关系S中的悬浮元组
下图分别为左外连接和右外连接:

3.4 除运算
- 给定关系R (X,Y) 和S (Y,Z),其中X,Y,Z 为属性组。
- R中的Y与S中的Y可以有不同的属性名,但必须出自相同的
域集。 - R与S的除运算得到一个新的关系P(X),
- P是R中满足下列条件的元组在 X 属性列上的投影:
- 元组在X上分量值x的象集Yx包含S在Y上投影的集合,记作:
R ÷ S = { t r [ X ] ∣ t r ∈ R ∧ π Y ( S ) ⊂ Y x } R÷S = \{ t_{r}[X] | t_{r}\in R ∧π_{Y}(S) \subset Yx \} R÷S={tr[X]∣tr∈R∧πY(S)⊂Yx}
Yx:x在R中的象集, x = t r [ X ] x = t_{r}[X] x=tr[X]

解析: - 在关系R中,A可以取四个值{a1,a2,a3,a4}
a1的象集为 {(b1,c2),(b2,c3),(b2,c1)}
a2的象集为 {(b3,c7),(b2,c3)}
a3的象集为 {(b4,c6)}
a4的象集为 {(b6,c6)} - S在(B,C)上的投影为
{(b1,c2),(b2,c1),(b2,c3) } - 只有a1的象集包含了S在(B,C)属性组上的投影
所以 R÷S ={a1}
总结
关系就是表
| 运算 | 符号 | 说明 |
|---|---|---|
| 并 | ∪ \cup ∪ | 取两个表的并集 |
| 交 | ∩ \cap ∩ | 取两个表的并集 |
| 差 | − - − | 前表去掉两个表的公共部分 |
| 笛卡尔积 | x | 生成一个a+b行,n*m列的新表(a,b为原来行数,m,n为原来列数) |
| 选择 | σ F ( R ) σ_{F}(R) σF(R) | 去除R中满足关系F的多个元组 |
| 投影 | π A ( R ) π_{A}(R) πA(R) | 在关系R中取出属性为A的列,去掉重复行 |
| 连接 | R ⋈ A θ B S R\mathop{\bowtie}\limits_{AθB} S RAθB⋈S | 两个集合有可以比较的l两列,然后连两个表1 |
| 除 | ÷ | 我的理解R中 包含 S中 的所有Y 的x |
自然连接时没有重复属性列的等值连接,外连接是补空值的自然连接 ↩︎






















 241
241











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








