梯度下降法理解

一个标量函数的梯度记为：

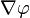 或 

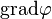
其中（nabla）表示矢量微分算子。

在三维情况，该表达式在直角坐标中扩展为：

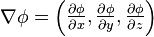
    一个多元函数的梯度方向是该函数值增大最陡的方向。对于一元函数而言，梯度方向是沿着曲线切线的，然后取切线向上增长的方向为梯度方向。对于二元或多元函数而言，梯度向量为函数F对每个变量的导数，该向量的方向就是梯度的方向。

    上图为一元二次函数的曲线图，可以看出：在最低点的左边部分，每一点的梯度方向值都是负值，因为每一点的斜率都是小于0的，所以当变量沿着梯度的方向递进，函数值越来越大，从上图可以很明显看出；同理右边，每一点的梯度方向都是大于0的，所以沿着梯度方向，函数值也是越来越大。所以，函数的梯度方向总是函数值越来越大的方向。因此，我们要想求最小值，就应该沿着梯度的反方向进行，这正是梯度下降法的原理。

下面是转载的一个简单例子，能够帮助去理解梯度下降法的整个运算过程：

我们知道，函数的曲线如下：

1. /* 
2.  * @author:郑海波 
3.  * blog.csdn.net/nuptboyzhb/ 
4.  * 2012-12-11 
5.  */  
6. #include <iostream>  
7. #include <math.h>  
8. using namespace std;  
9. int main()  
10. {  
11.     double e=0.00001;//定义迭代精度  
12.     double alpha=0.5;//定义迭代步长  
13.     double x=0;//初始化x  
14.     double y0=x*x-3*x+2;//与初始化x对应的y值  
15.     double y1=0;//定义变量，用于保存当前值  
16.     while (true)  
17.     {  
18.         x=x-alpha*(2.0*x-3.0);  
19.         y1=x*x-3*x+2;  
20.         if (abs(y1-y0)<e)//如果2次迭代的结果变化很小，结束迭代  
21.         {  
22.             break;  
23.         }  
24.         y0=y1;//更新迭代的结果  
25.     }  
26.     cout<<"Min(f(x))="<<y0<<endl;  
27.     cout<<"minx="<<x<<endl;  
28.     return 0;  
29. }