UVA-679（完全二叉树）Dropping Balls

原题链接： UVA-679

测试样例

Sample Input
5
4 2
3 4
10 1
2 2
8 128
-1
Sample Output
12
7
512
3
255

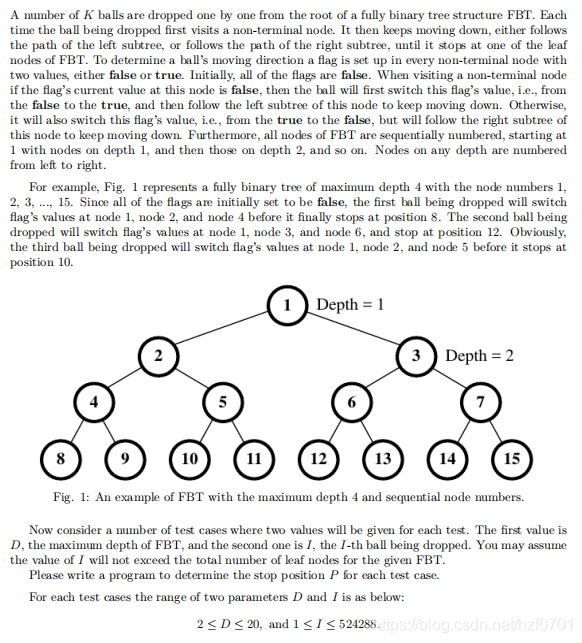
题意： 有一颗完全二叉树，最大深度为$D$。所有节点从上到下从左到右依次编号$1,2,3,4,...,2^D-1$。在根节点处放下一个小球，它会往下落。而每个节点都有一个开关，若开关打开则小球往右走，否则小球往左走。直到走到叶子结点。现在有$I$个小球顺序下落，求第$I$个小球落在的叶子结点编号。

解题思路： 首先在解这道题之前我们要知道这种顺序编号树的规律。即对于一个节点$k$，那么其左右节点编号依次为$2k$和$2k-1$。这个结论非常重要，是解题的关键。 OK，这道题我们可能很容易想到模拟，最后得到最后一个球的所在叶子节点的编号。但我们要知道的一点就是时间复杂度会非常大，这并不适用。那么我们在思考一下，如果假设到达一个节点的前两个球，它们必定是一个在左子树，而一个是在右子树，所以我们只需要看球的编号，我们发现奇数编号的球一定是在左子树，而偶数编号的球一定是在右子树，故我们可以直接模拟最后一个球的路线。（这实际上在模拟一个向左向右球的过程，根据深度$d$，我们下落次数为$d-1$次，故我们只要模拟$d-1$次即可。）具体看AC代码。

AC代码

/*
*blog:https://blog.csdn.net/hzf0701
*邮箱：unique_powerhouse@qq.com
*注：文章若有任何问题请私信我或评论区留言，谢谢支持。
*/
#include<bits/stdc++.h>
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)

using namespace std;

typedef long long ll;
const int maxn=20;//数组所开最大值
const int mod=1e9+7;//模
const int inf=0x3f3f3f3f;//无穷大

int t,d,i;
void solve(){
    int k=1;
    rep(j,0,d-2){
        //对于每一层判断，此时这个球是第几个球
        if(i%2){
            //说明向左的球。
            k*=2,i=(i+1)/2;
        }
        else{
            k=k*2+1,i=i/2;
        }
    }
    cout<<k<<endl;
}
int main(){
    while(cin>>t&&t!=-1){
        while(t--){
            cin>>d>>i;
            solve();
        }
    }
    return 0;
}