何为背包问题
对动态规划问题有所了解的同学一定都听说过背包问题(Knapsack problem)。
在动态规划(Dynamic Programming)问题中,最典型的是斐波那契(Fibonacci)数列,即有一串符合1,1,2,3,5,8,11......规律变化的数列,每一项的值都为前两项之和,要求给出第n位上的
数字,递推式为f(n) = f(n-1) + f(n-2)。
而背包问题即是在此基础上引入多个变量,综合分析并推导出最优解的一类问题。解决背包问题同样需要利用动态规划的分析方法,寻找递推关系并定义数组以逐步推导。
这样说可能有些抽象,以接下来要说的01背包问题为例,题目给出了两组数据,分别是若干件物品的体积V(Volume)与价值W(Worth),给出背包的总体积,求能装下的物品的最大价值。
对于这一问题,我们很明显不能只追求其中一个变量的最优化,例如我们不能只考虑物品的价值,因为价值大的物品体积也可能很大,而应当针对各个物品选与不选的情况进行分别讨论,以获取在满足体积限制的条件下所能获取的最大价值。
本文是背包问题的简单入门,接下来我将讲述01背包与完全背包这两种基础背包问题的解法与相关优化。
01背包问题
原题链接:https://www.acwing.com/problem/content/2/
基本描述
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量且总价值最大,并将最大的价值输出。
输入格式第一行两个整数 N,V 用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi 用空格隔开,分别表示第 i 件物品的体积和价值。
数据范围0 < N,V ≤ 10000 < N,V ≤ 1000
0 < vi,wi ≤ 1000
输入样例4 5 1 2 2 4 3 4 4 5输出样例
8
题意解析
相信部分同学已经读懂了题意,读不懂也没事,接下来我们以测试样例为例来理解一下本题的意思。
在本题中给出的数据有:
-
物品的数量N(4)
-
背包的容量V(5)
-
每件物品的体积与价值(下面以表格的形式呈现)
| 体积 | 价值 | |
|---|---|---|
| 物品1 | 1 | 2 |
| 物品2 | 2 | 4 |
| 物品3 | 3 | 4 |
| 物品4 | 4 | 5 |
据此我们理解题目要求在满足物品的总体积不大于背包的容量V(5)的前提下所能获取的最大价值
例如:
-
若选择物品1和物品2,则总体积为3 (小于5) ,总价值为6;
-
若选择物品2和物品3,则总体积为5 (等于5),总价值为8…
对多种符合条件的可能性进行分析计算,最终得出所能获取的最大价值为8。
思路点拨
我们都知道,背包问题是一道典型的动态规划问题,而解决动态规划问题,一个最朴素的想法就是分析每一种决策的依赖关系、并由此推导出状态转移的递推式。
例如经典的斐波那契数列,从第三位开始,每一个数都依赖于前两个数的值、等于前两个数之和,因此我们很容易得出递推式为f(n) = f(n-1) + f(n-2)。
回到我们的背包问题,我们不妨这样思考:再假设前N-1个物品已经取得最大价值的前提下考虑第N个物品的决策,对于第N件物品我们无非只有要与不要两种选择,
- 若要,则以付出第N件物品的体积为代价获得第N件物品的价值;
- 若不要,则前N件物品的能获取的最大价值就等于前N-1件物品。
那么,我们怎么来确定第N件物品到底是要还是不要呢?很简单,我们仅需对要与不要两种决策的结果进行比较即可。
这时候可能有一个思维误区,就在于如果对要与不要两种决策的结果进行比较的话,那么
在前期背包容量足够的情况下,要该物品不是一定会比不要获取更高的价值吗?
的确,考虑到这个问题,我们需要让背包的容量一点点变大,这样才有利于在后续的状态转移中将所有的可能性都考虑到。
可能有些同学还是有疑惑,没关系,我们先把这个问题放一放,先来考虑dp数组的确定。
分析过程
首先,我们要将题目给出的数据先录入,我们可以先定义两个变量n,m来获取物品的数量以及背包的容量;再定义两个全局数组v[i]来分别存放物品的体积,w[i]来分别存放物品的价值。
其次,我们需要一个能够对动态转移的值进行判断的数组,对于本题,我们不妨设一个二维数组dp[i][j]以表示只考虑前i个物品且背包的容量为j时所能获取的最大价值。
例如,dp[i][0]就表示只考虑前i个物品且背包容量为0时所能获取的最大价值,很显然,dp[i][0]的值为0,因为背包的容量为0,意味着无法装下任何东西,能获取的价值自然就只能是0了。
有了这些数值后,我们就可以推导本题的转移方程了,因为对第N个物品,仅需考虑要与不要两种情况。
如果不要,则前N件物品的能获取的最大价值就等于前N-1件物品,即dp[i][j] = dp[i - 1][j];
而如果要,则需要以付出第N件物品的体积为代价获得第N件物品的价值,即dp[i][j] = dp[i - 1][j - v[i]] + w[i])
这时候要想判断那种决策所获取的价值更大,只需要对两种决策产生的结果进行判断、选择哪个更大的即可,即
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
确定了这些以后,我们只需知道最终结果存放在哪里并将其输出即可,对于本题,我们所需要得到的结果是在考虑所有物品且用上背包容量时所能获取的最大价值,即dp[n][m]
状态转移
其实确定了以上信息后我们就已经可以开始程序的编写了,但为了让大家更直观地理解这个过程,我们来看一下具体的状态转移图。
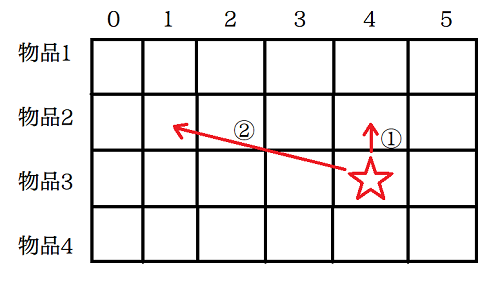
我们假设现在对dp[3][4]的值进行探讨,根据上文的分析,此时应当存在两种情况,即要与不要。
-
若不要,则
dp[3][4]应等于dp[2][4],即如图中箭头①所示; -
若要,物品3的体积
v和价值w分别为3、4,可知dp[3][4]应等于dp[2][4-3]+4,即dp[2][1]+4,依赖于dp[2][1]的值,如图中箭头②所示;
由此我们可以解答上面提出的问题,即
如果对要与不要两种决策的结果进行比较的话,那么在前期背包容量足够的情况下,要该物品不是一定会比不要获取更高的价值吗?
从图中我们可以看出,每一个位置的值都受到另外两个位置的影响,而两个位置并不是确定的,它受到物品N体积与价值的影响,因
此我们只需让让背包的容量一点点变大,考虑的物品一点点增多,即可考虑到所有可能的情况,并从中求出最大价值。
代码实现
C++代码实现如下:
带注释版:
#include <iostream>
using namespace std;
const int MAXN = 1010; // 数组的大小,取值稍大于数据范围即可
int v[MAXN]; // 体积V (Volume)
int w[MAXN]; // 价值W (Worth)
int dp[MAXN][MAXN]; // dp[i][j]表示只考虑前i个物品且背包的容量为j时所能获取的最大价值
// 注意:在C++中若数组未赋初值则默认初值为0,因为dp[i][0]的值一定为0,后续仅需让i与j都从1开始循环即可
int main()
{
int n, m;
cin >> n >> m; // n与m分别录入物品的个数以及背包的最大容量
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i]; // 循环录入各个物品的体积与价值
for(int i = 1; i <= n; i++) // 外循环让i不断递增,即每轮循环考虑更多的物品
for(int j = 1; j <= m; j++) // 内循环让j不断递增,即可供使用的背包容量不断上升
{
// 若容量不够,则dp[i][j]只能等于dp[i - 1][j];
if(j < v[i])
dp[i][j] = dp[i - 1][j];
// 能容量足够,需进行决策是否选择第i个物品
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
}
cout << dp[n][m] << endl; //按照上文分析,输出dp[n][m]的值即可
return 0;
}
纯净版:
#include <iostream>
using namespace std;
const int MAXN = 1010;
int v[MAXN];
int w[MAXN];
int dp[MAXN][MAXN];
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
if(j < v[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
}
cout << dp[n][m] << endl;
return 0;
}
优化方案
考虑优化方案一般从时间复杂度与空间复杂度两个角度入手。
对于本题来说,由于我们必须让考虑物品的数量与背包的容量一点点变大,所以两层循环是必不可少的,时间复杂度无法优化。
而空间复杂度则存在优化的方案,在于我们可以采用一维数组来代替二维数组以节省空间。
我们首先想想,如果一天早上有人问你 " 晚上睡得好吗? ” 我们一定会理解为 “ 昨天晚上睡得好吗?” ,因为今天晚上还没到。
同样地,对于本题,因为dp[i](考虑物品的数量)只影响层与层之间的更新,那么在默认未更新的情况下就可以将其省略。
这样,原先的二位数组dp[i][j]就变成了dp[j](背包容量为j时所能获取的最大价值)。
值得注意的是,因为赋值操作实际上是将等号右边处理好后赋值给等号左边,所以
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
等号右边的值实际上是从上一层继承下来的,而计算后赋值给等号左边才完成了层之间的更新,因而与用i和i-1标识的方法效果相同。
但与优化前不同的是,优化后的j必须逆序变化(注意只是j,外层循环中i同样正序变化),
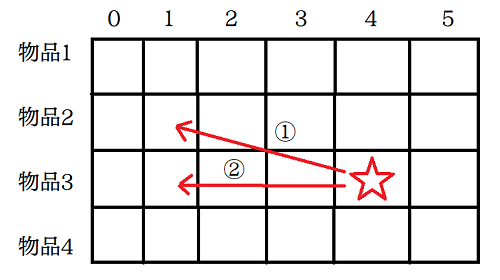
因为如图所示,在选择要该物品的情况下,我们想得到的是箭头①的依赖关系,而因为我们将数组降为一维,数组中的值是在不断更新的。
若j从小到大变化,则对于每一层j都从1到5依次变化,dp[4](即图中五角星处)按箭头①所依赖的dp[1]在循环过程中被更新了,导致dp[4]将错误地依赖于箭头②;
而如果从大到小变化,则对于每一层j都从5到1依次变化,对dp[4]进行更新时dp[1]的值仍来自于上一层,维持了箭头①的依赖性。
因此,我们必须让j逆序变化。
优化后的代码实现
C++代码实现如下:
带注释版:
#include <iostream>
using namespace std;
const int MAXN = 1010;
int dp[MAXN];
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
int v, w;
cin >> v >> w; // 循环中每考虑一个新的物品就对体积与价值的值进行更新,节省了原先数组的空间,边更新边处理
for(int j = m; j >= v; j--) // j小于v将无法装下该物品,固不讨论
dp[j] = max(dp[j], dp[j - v] + w);
}
cout << dp[m] << endl;
return 0;
}
纯净版:
#include <iostream>
using namespace std;
const int MAXN = 1010;
int dp[MAXN];
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
int v, w;
cin >> v >> w;
for(int j = m; j >= v; j--)
dp[j] = max(dp[j], dp[j - v] + w);
}
cout << dp[m] << endl;
return 0;
}
参考资料
【1】崔添翼 . 背包问题九讲






















 1244
1244











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








