理解皮尔逊相关系数（Pearson Correlation Coefficient）

要理解Pearson相关系数，首先要理解协方差（Covariance），协方差是一个反映两个随机变量相关程度的指标，如果一个变量跟随着另一个变量同时变大或者变小，那么这两个变量的协方差就是正值，反之相反，公式如下：

$$cov(x,y) = \dfrac{ \sum_{i=1}^n (x_{i}-x_{μ})(y_{i}-y_{μ}) }{n-1}$$
Pearson相关系数公式如下：
$$p_{x,y}=cor(x,y)=\dfrac{cov(x,y)}{δxδy}=\dfrac{E[(x-x_{μ})(y-y_{μ})]}{δxδy}$$
由公式可知，Pearson相关系数是用协方差除以两个变量的标准差得到的，虽然协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），但是协方差值的大小并不能很好地度量两个随机变量的关联程度，例如，现在二维空间中分布着一些数据，我们想知道数据点坐标X轴和Y轴的相关程度，如果X与Y的相关程度较小但是数据分布的比较离散，这样会导致求出的协方差值较大，用这个值来度量相关程度是不合理的。
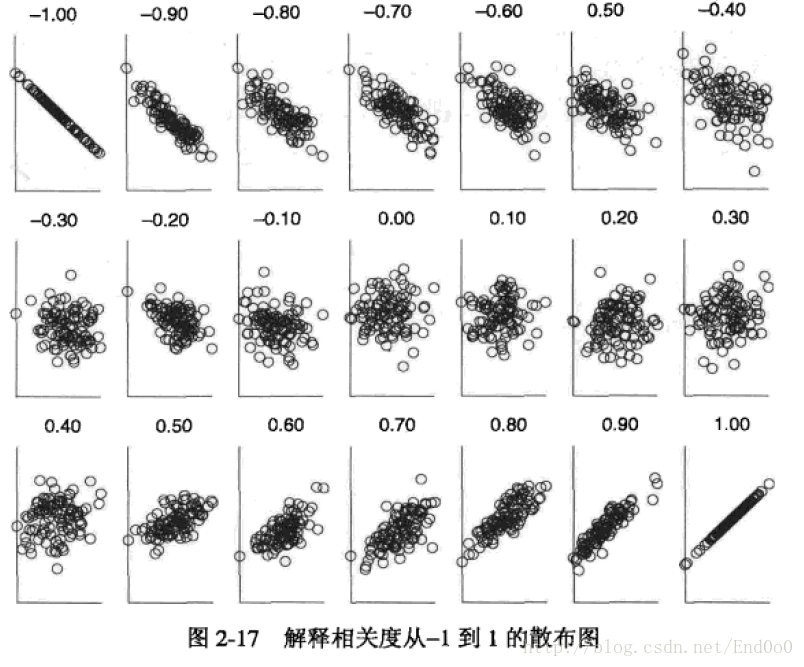
为了更好的度量两个随机变量的相关程度，引入了Pearson相关系数，其在协方差的基础上除以了两个随机变量的标准 $δ^2=\dfrac{\sum_{i=1}^n(x_{i}-x_{μ})}{n}$，容易得出，pearson是一个介于-1和1之间的值，当两个变量的线性关系增强时，相关系数趋于1或-1；当一个变量增大，另一个变量也增大时，表明它们之间是正相关的，相关系数大于0；如果一个变量增大，另一个变量却减小，表明它们之间是负相关的，相关系数小于0；如果相关系数等于0，表明它们之间不存在线性相关关系。《数据挖掘导论》给出了一个很好的图来说明：