目录
1. 递归变非递归
二叉树的三种遍历方法都是递归的,但也可以修改为非递归
1.1 先序遍历
入栈顺序:头 右 左

1.2 后序遍历
入栈顺序: 头 右 左

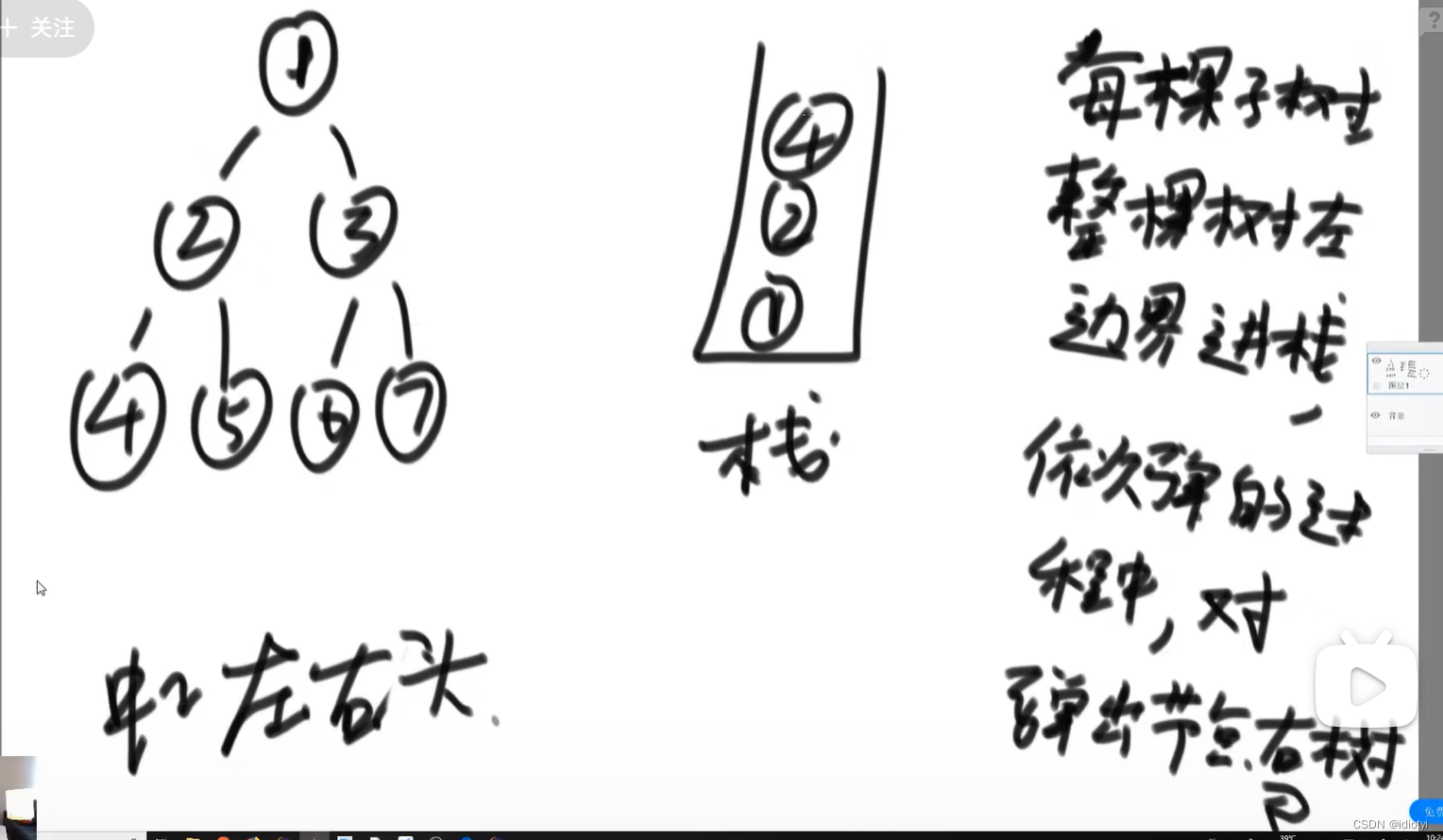
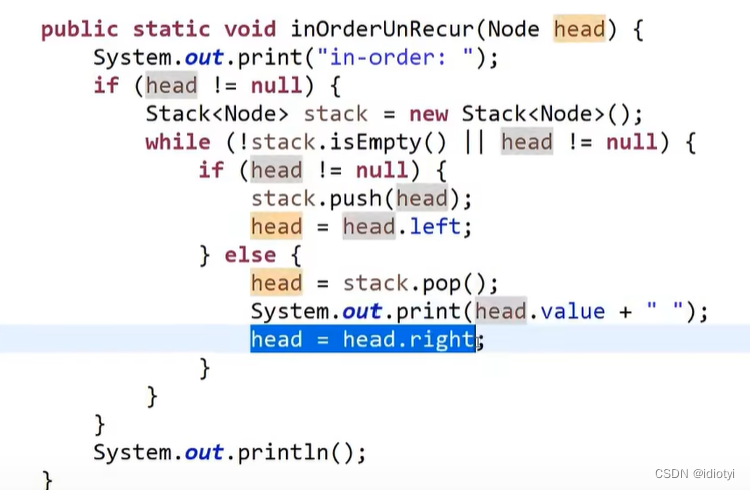
1.3 中序遍历
入栈顺序:左右头
每压一个节点入栈,如果他有左分支,需要把左分支这条直线也入栈
2. 二叉树的遍历
2.1 宽度遍历
使用队列(先进先出),弹出一个数,然后放其左再放右进去队列
题目:求一个二叉树的最大宽度
解:关键代码

循环结束后还需要和最后一层比一下
3. 搜索二叉树
定义:左节点都比它小,右节点都比它大
4. 题目
4.1 判断树
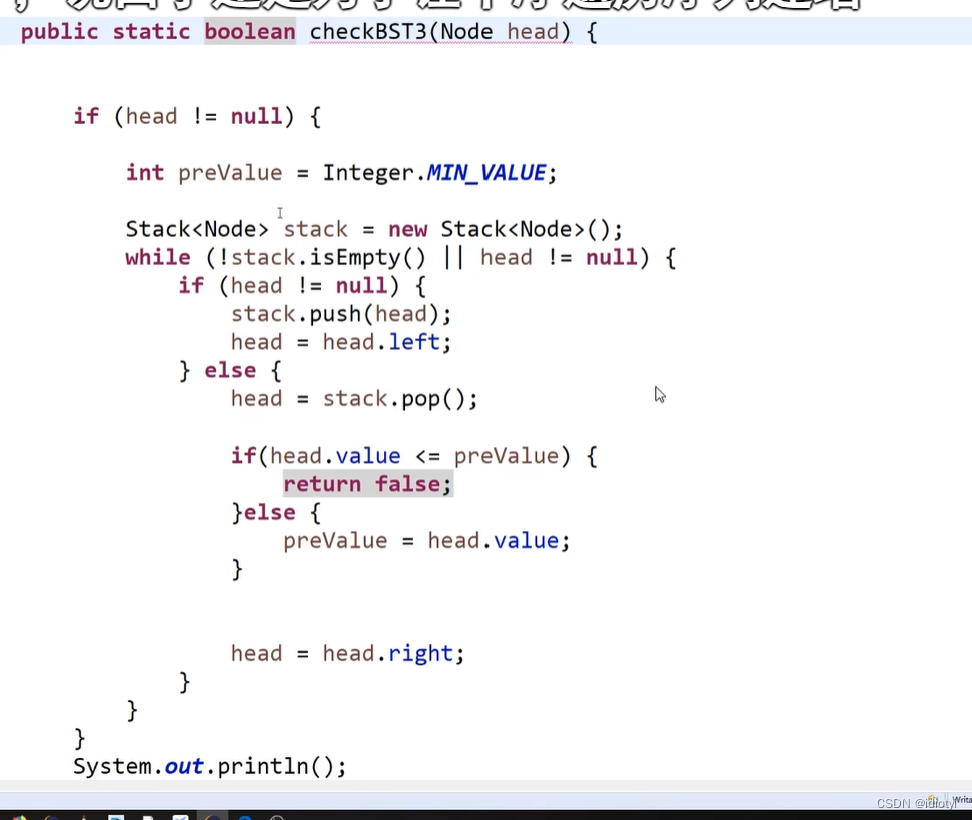
(1)判断是不是搜索二叉树
判断一棵树是不是中序遍历使用中序遍历就行
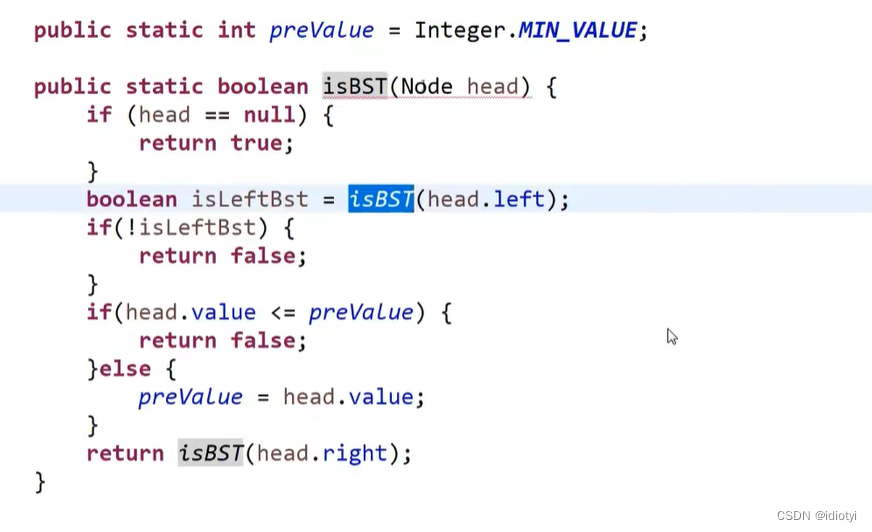
注意preValue是全局变量
先一直遍历到最后一棵左子树(过程中preValue一直不变),然后preValue变成最后一棵左子树的head(preValue<head),此时遍历head的右子树(右节点>preValue(head)),依次往上。每次preValue先变成左节点,再变成head(上一层的左节点)
(2)判断是不是完全二叉树
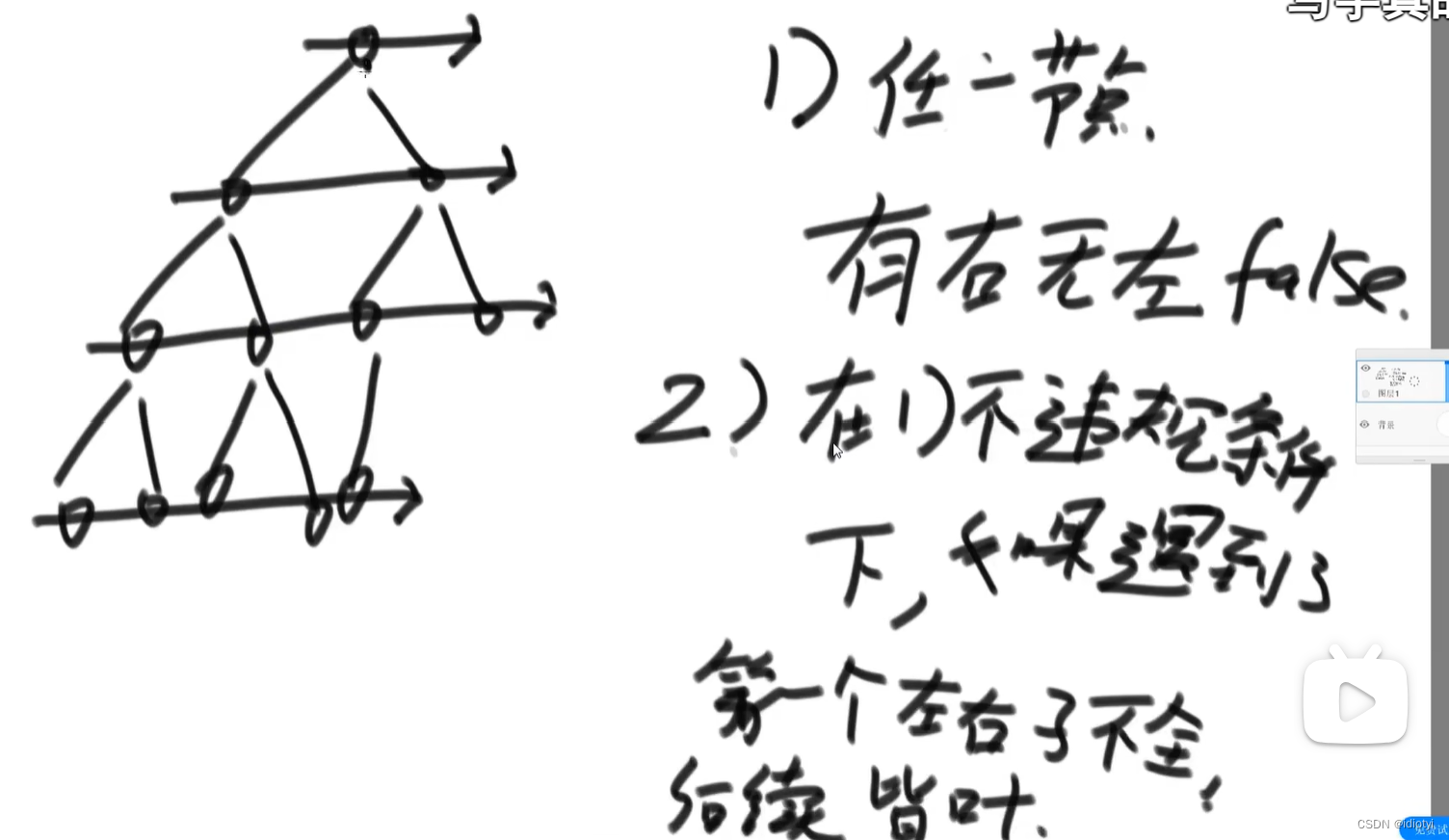

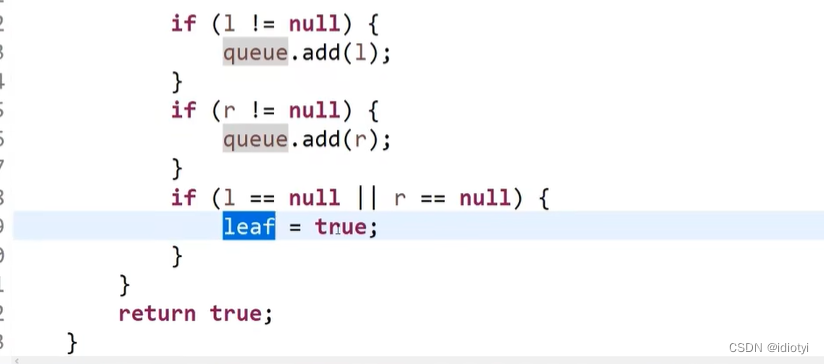
(3)判断满二叉树
- 统计最大深度L和节点个数N,是否满足N=2^L-1
(4)判断平衡二叉树
任一子树,左右树高度差不超过1

4.2 最低公共祖先

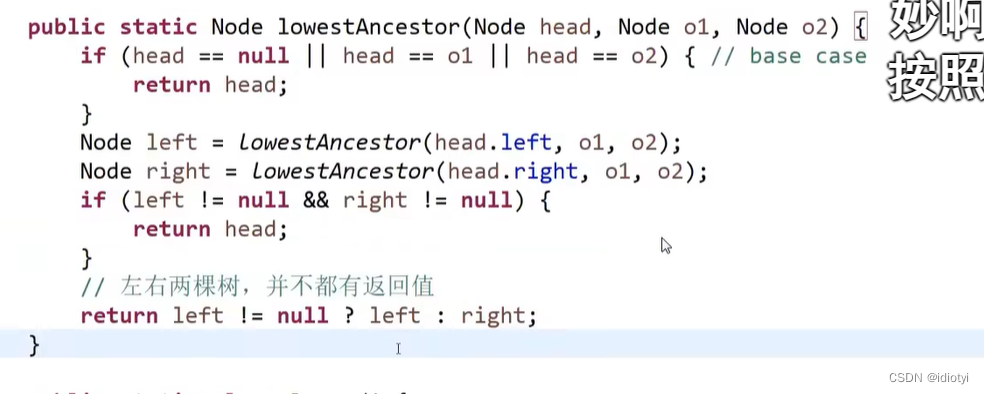
4.3 求后继节点
即中序遍历的后一个节点
(1)x如果有右树,右数上的最左节点为后继节点
(2)x无右树,往上找,直到寻找到某一层的左节点

4.4 二叉树的序列化和反序列化

先序遍历序列化:
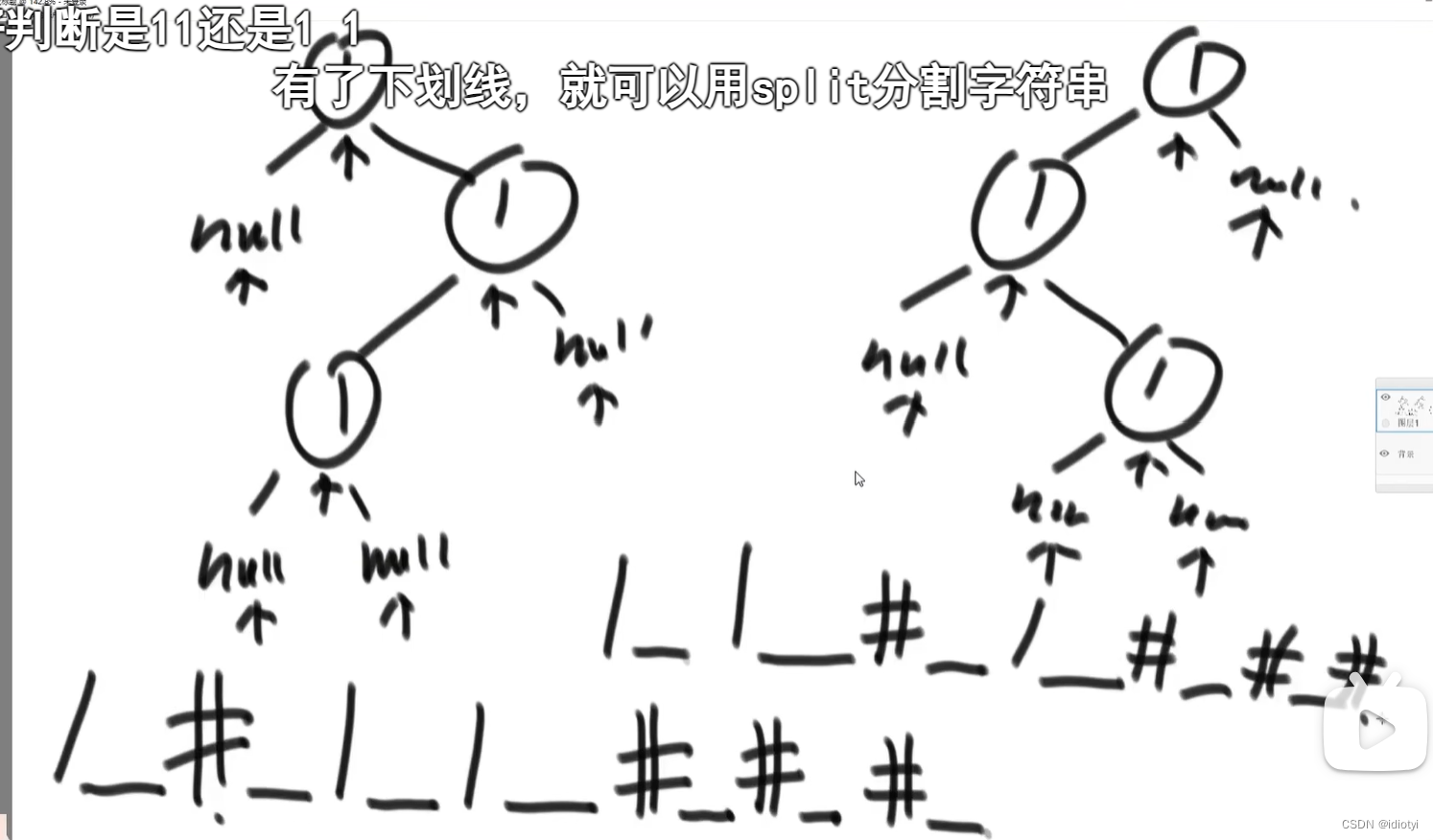
4.5 纸条对折问题
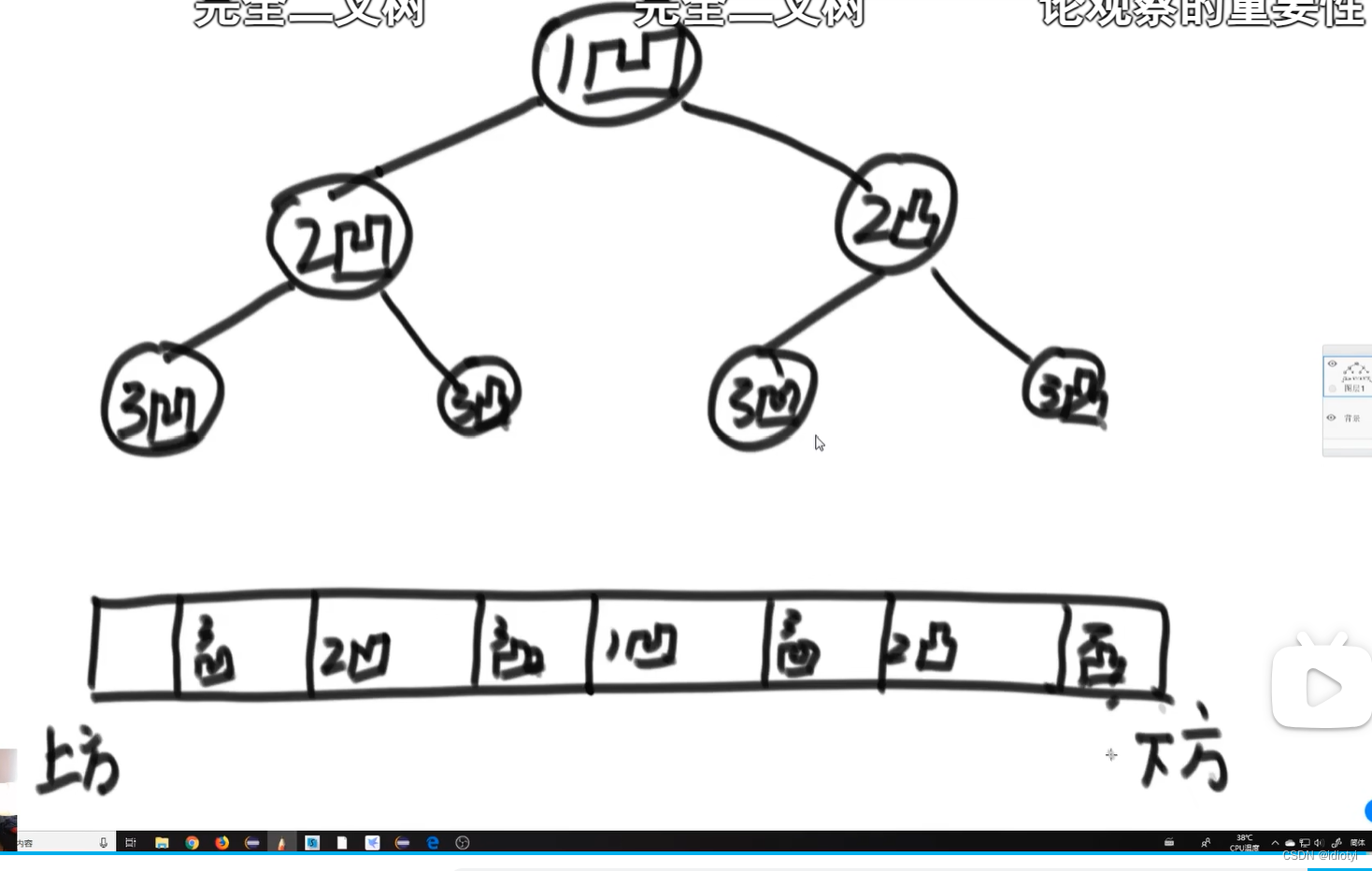
5. 树形DP
分别讨论左右子树应该满足什么条件以及应该返回什么信息
如递归判断搜索二叉树:
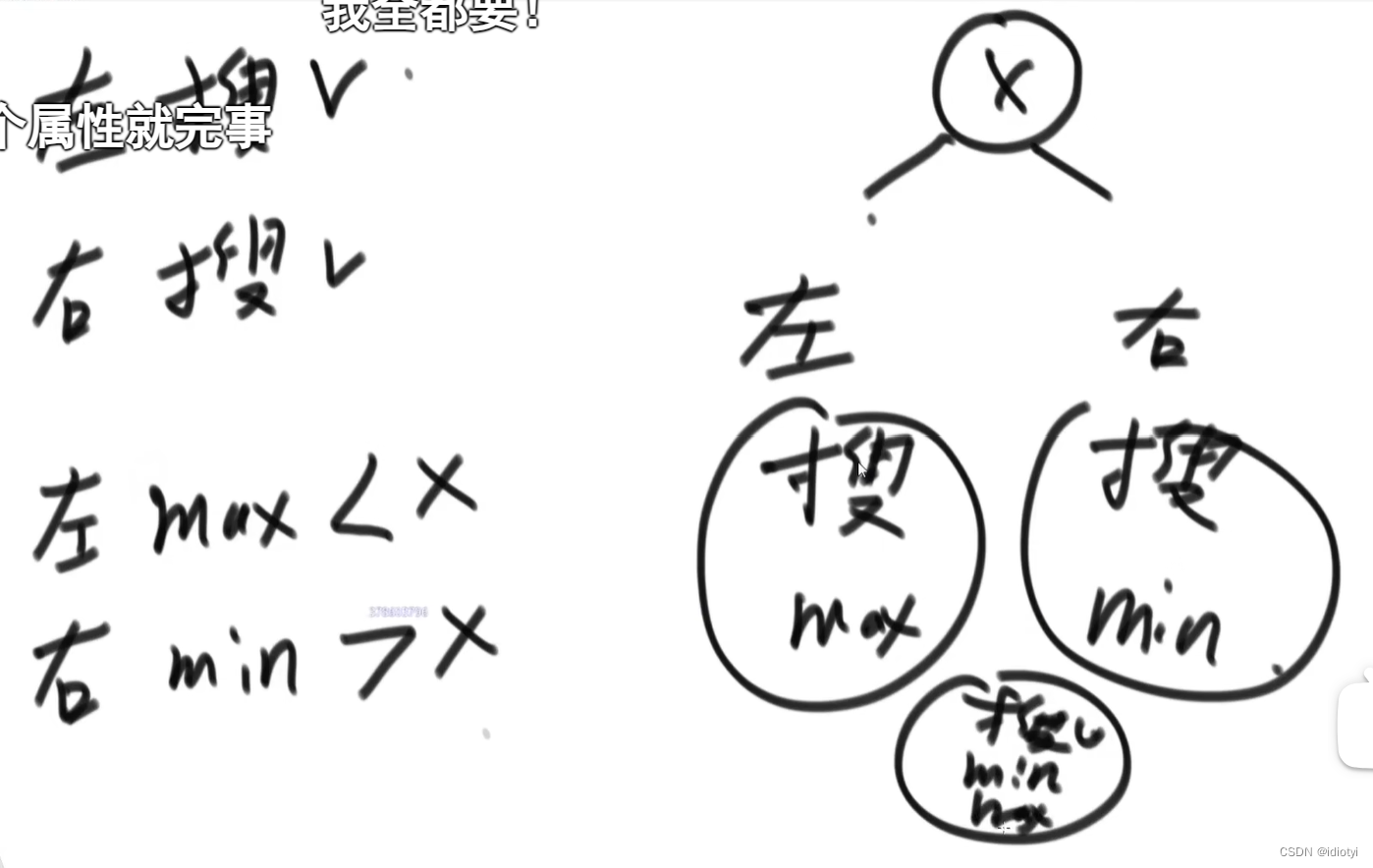

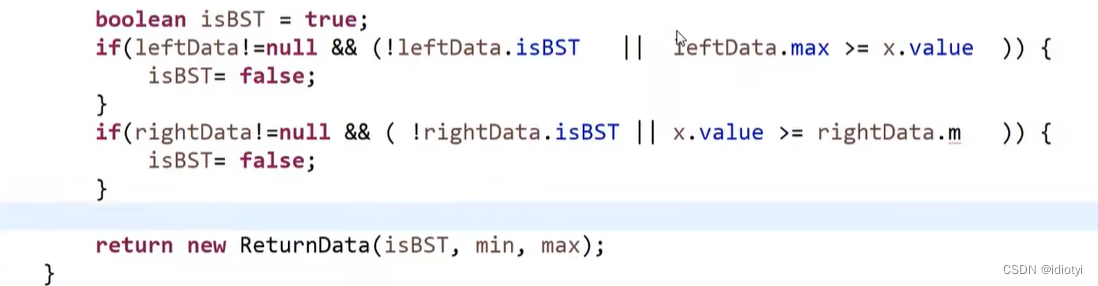






















 645
645











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








