第一章关于初等的计算方法,涉及数值微分、数值积分、排序算法、插值、数值求根、数值求极值的python实现。
目录
(4)偏微分差分
2. 冒泡排序
4. 样条插值
一、数值微分
1. 差分公式
(1)一阶差分
前向差分:,精度为1阶
对称中心差分:,精度为2阶
五点差分:,精度为4阶
(2)二阶差分
,精度为2阶
(3)三阶差分
,精度为3阶
(4)偏微分差分
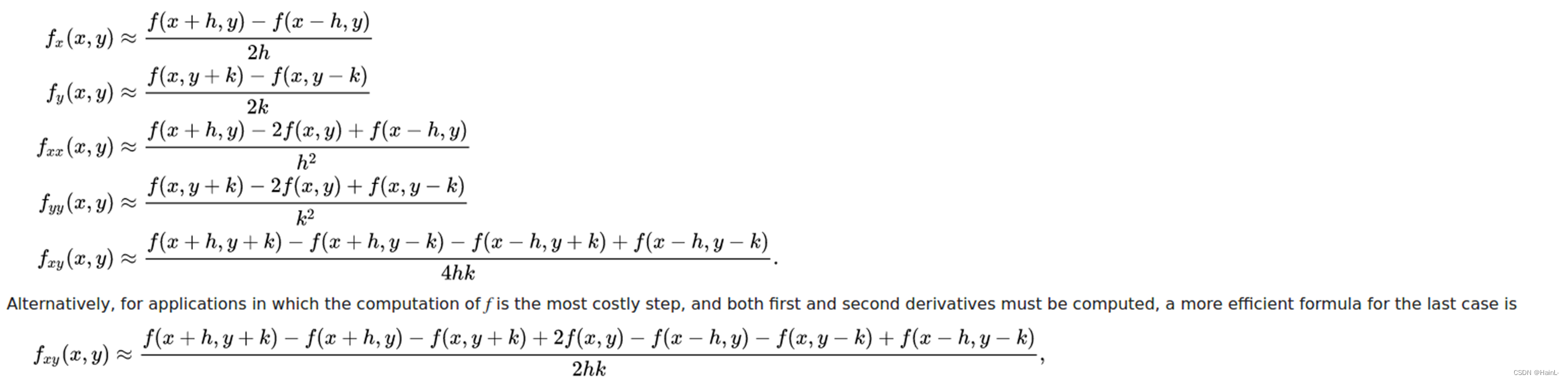
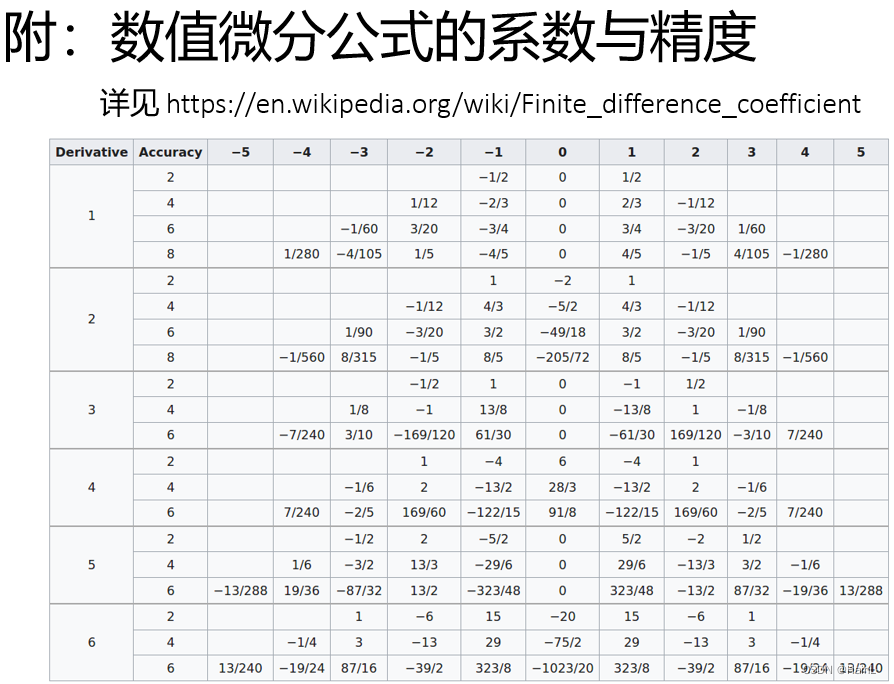
2. 误差
误差分为舍入误差和近似误差
舍入误差:运算得到的近似值和精确值之间的差异。原因是数值类型有限位精度。对python而言,浮点数精度大概为。
近似误差:数值计算公式是一个近似的结果,计算的步长不可能无限小,从而导致误差。
3. 代码示例
例:以函数,用三种一阶差分方式,分别选取步长1e-3、1e-5和1e-8,比较误差。
(1)画出数值微分曲线
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题
x = lambda t : np.exp(t/2)*np.cos(t)
dxdt= lambda t : np.exp(t/2)*(1/2*np.cos(t)-np.sin(t))
def nd(f,x,method=None,h=None): #定义数值微分方程
if method=='前向差分':
return (f(x+h)-f(x))/h
if method=='中心差分':
return (f(x+h)-f(x-h))/(2*h)
if method=='五点差分':
return (-f(x+2*h)+8*f(x+h)-8*f(x-h)+f(x-2*h))/(12*h)
t=np.linspace(0,20,200)
hs=[1e-3,1e-5,1e-8]
methods=['前向差分','中心差分','五点差分']
fig, axs = plt.subplots(3,3, figsize=(16,10))
for i in range(3):
for j in range(3):
axs[i,j].plot(t,dxdt(t))
axs[i,j].plot(t,nd(x,t,method=methods[i],h=hs[j]),ls='--',label='数值微分')
axs[i,j].set_title('{0}法,步长为{1}'.format(methods[i],hs[j]))
axs[i,j].legend(frameon=False)
fig.tight_layout()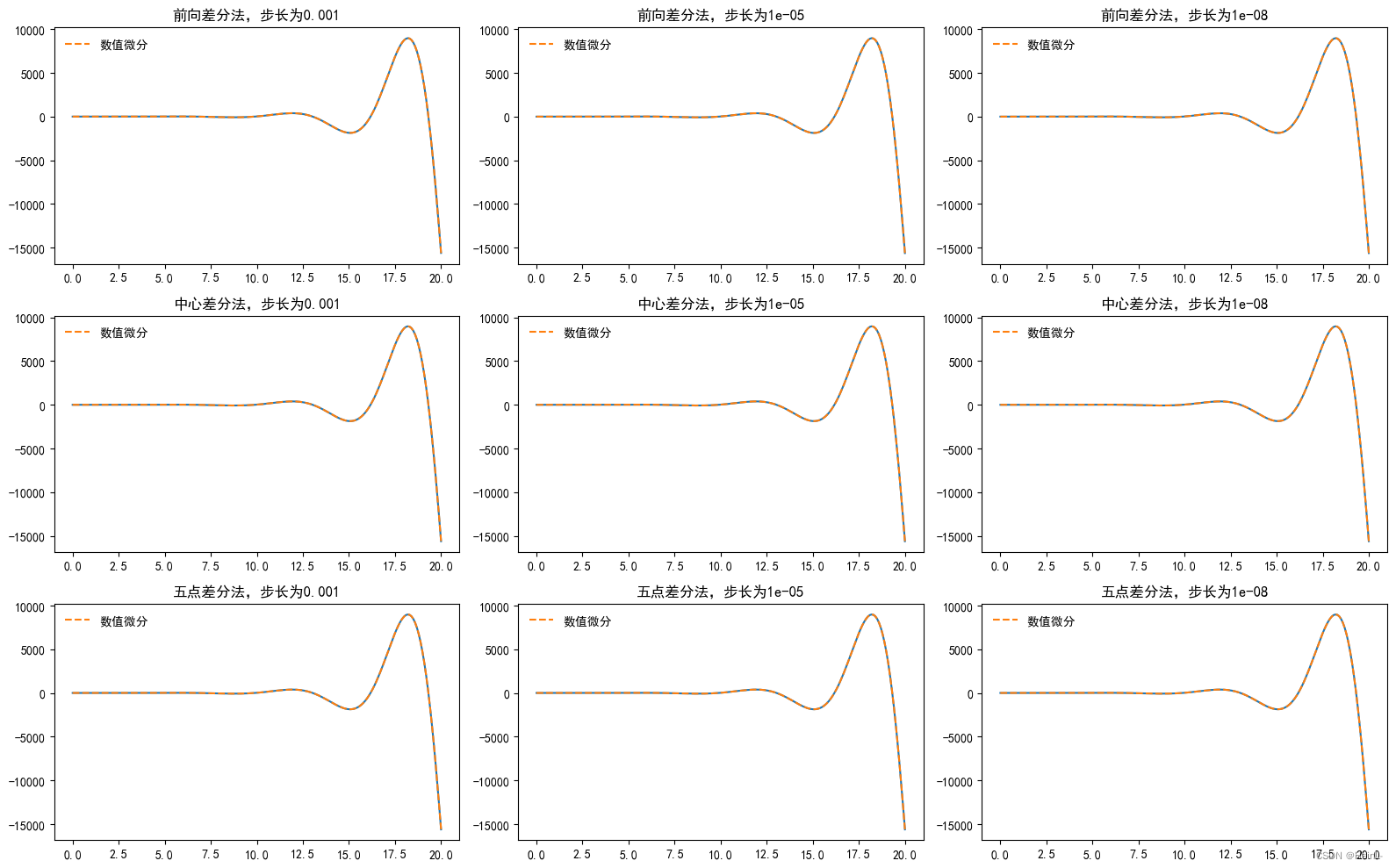
(2)画出误差曲线
#继续上述代码
fig, axs = plt.subplots(3,3, figsize=(16,10))
for i in range(3):
for j in range(3):
axs[i,j].plot(t,dxdt(t)-nd(x,t,method=methods[i],h=hs[j]))
axs[i,j].set_title('{0}法,步长为{1}'.format(methods[i],hs[j]))
axs[i,j].set_ylabel('误差')
fig.tight_layout()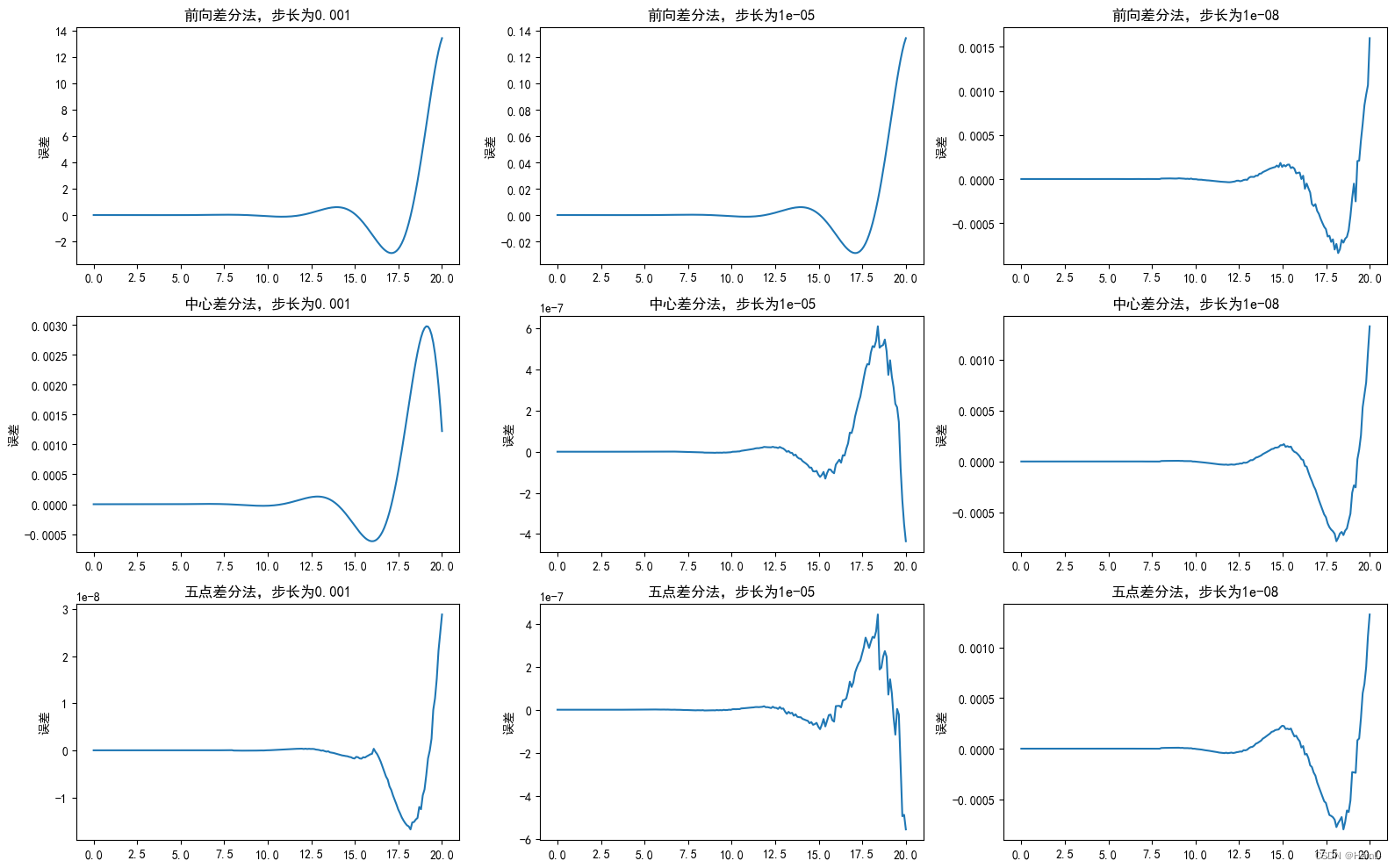
二、复杂度与排序算法
1. 时空复杂度&空间复杂度
我们通常从算法所占用的「时间」和「空间」两个维度去衡量不同算法之间的优劣。
•时间维度:是指执行当前算法所消耗的时间,用「时间复杂度」来描述。
•空间维度:是指执行当前算法需要占用多少内存空间,用「空间复杂度」来描述。
空间复杂度和时间复杂度是从量级进行估计的,常见的有:
•常数阶 O(1)
•对数阶 O(logN)
•线性阶 O(N)
•线性对数阶 O(N logN)
•平方阶 O()
•k次方阶 O()
•指数阶 O()
例:
时间复杂度O(N)
for i in range(N):
j=i
j+=1时间复杂度O()
for x in range(N):
for i in range(N):
j=i
j+=1空间复杂度O(N)
for i in range(N):
a[i] = i接下来我们从时间复杂度的角度判断两种排序算法的优劣:冒泡排序和快速排序。
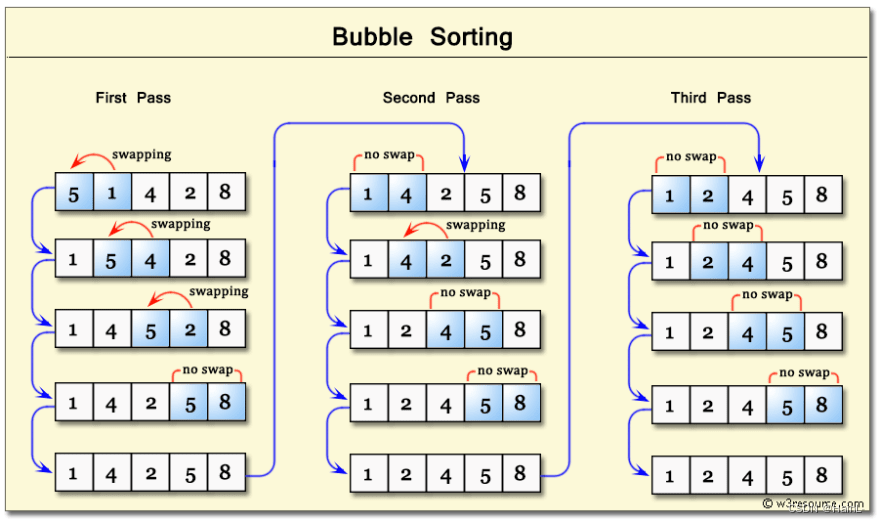
2. 冒泡排序
冒泡排序是一种简单的排序算法,它重复地从左往右遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就交换位置,直到没有再需要交换的元素。
冒泡排序的时间复杂度为O()
代码(用到了布尔变量的标记作用,见本笔记序章)
def bubble_sort(array):
# 外层循环遍历整个数组,从第一个元素到倒数第二个元素
for i in range(len(array)-1):
# 布尔变量swap用于标记是否发生了交换
swap = False
# 内层循环从数组开头到未排序部分的倒数第二个元素
for j in range(len(array)-1-i):
# 如果前一个元素大于后一个元素,交换它们的位置
if array[j] > array[j+1]:
array[j], array[j+1] = array[j+1], array[j]
swap = True # 标记发生了交换
# 如果某次遍历未发生交换,意味着数组已经排序完成,可提前结束循环
if not swap:
break
return array # 返回排序后的数组
#————————————————
#版权声明:来自CSDN博主「欢喜躲在眉梢里」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
#原文链接:https://blog.csdn.net/m0_52165864/article/details/1258998633. 快速排序
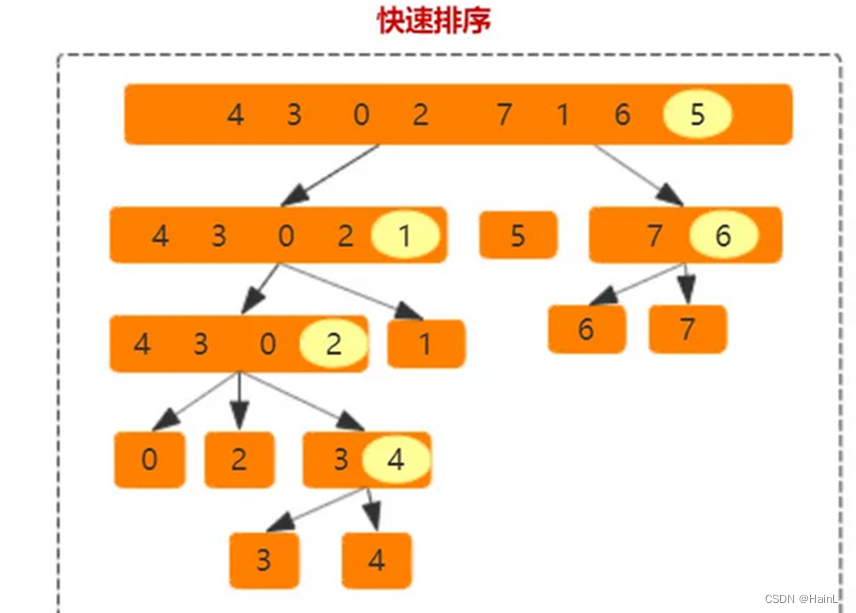
通过多次比较和交换来实现排序,流程如下:
1.首先设定一个分界值,以便将数组分成左、右两部分
2.将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边
3.然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,右侧的数组数据也可以做类似处理
4.重复上述过程
可以看出,这是一个递归算法。
快速排序的平均时间复杂度是O(),平均空间复杂度为O(
)
快排被认为是目前最好的内部排序方法。
代码
def partition(li,left,right):
tmp = li[left] #取最左边的值为参考值
while left < right:
while left < right and li[right] >= tmp: #从右边找比参考值tmp小的数,放到左边
right -= 1 #没有比参考值小就继续从右往左查找
li[left] = li[right] #找到了,就把右边的值写到左边空位上
while left < right and li[left] <= tmp: #同理找左边比参考值大的地方,放到右边
left += 1
li[right] = li[left] #把左边的值写到右边空位上
li[left] = tmp #把tmp归位
return left #返回最后左边查找到的地方,作为快排的分界点
def quick_sort(li,left,right): #递归地不断对基准值两侧进行分割排序
if left < right :#递归条件发生
mid = partition(li,left,right) #分界点
quick_sort(li,left,mid-1)
quick_sort(li,mid+1,right)
#————————————————
#版权声明:来自CSDN博主「想成大神的大艳」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
#原文链接:https://blog.csdn.net/qq_51201337/article/details/123322027三、插值
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x=list(np.random.randint(-20,20,5))
y=list(np.random.randint(-20,20,5))
x
<< [-16,-4,-12,13,-18]
y
<< [15,-7,1,18,1]
xdense=np.linspace(-18,13,1000)下面我们尝试用scipy的interpolate函数进行不同类型的插值
1. 拉格朗日插值

如:
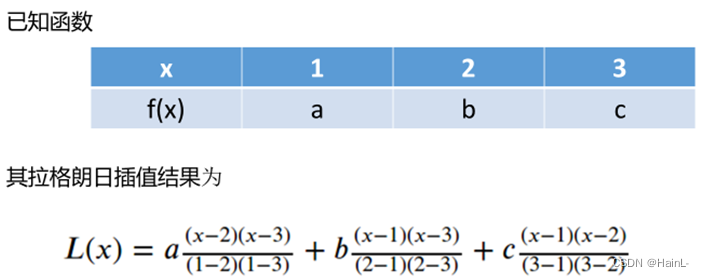
poly1=interpolate.lagrange(x,y) #拉格朗日插值
print(poly1)
plt.scatter(x,y)
plt.plot(xdense,poly1(xdense))
<<
4 3 2
-0.004634 x - 0.09182 x + 0.6065 x + 15.94 x + 42.37得到插值结果为:
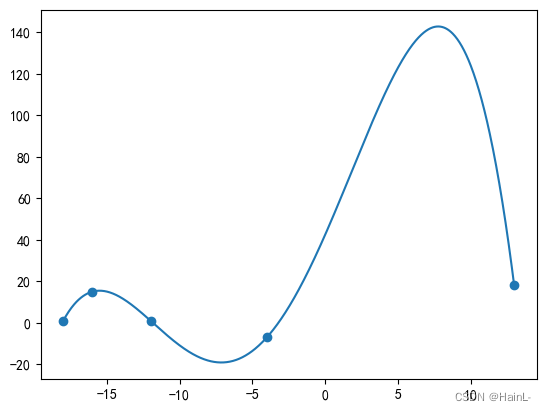
2. 分段插值
分段插值是将相邻多个插值点划为一区间,对所有区间分别进行插值。
一阶(线性)分段插值:得到每两个点之间的折线组成的分段函数
poly21=interpolate.interp1d(x,y,'linear') #一阶(线性)分段插值
plt.plot(xdense,poly21(xdense))
二阶分段插值:得到每三个点组成的区间的二次曲线函数,构成分段插值函数
poly22=interpolate.interp1d(x,y,'quadratic') #二阶分段插值
plt.plot(xdense,poly22(xdense))
plt.scatter(x,y)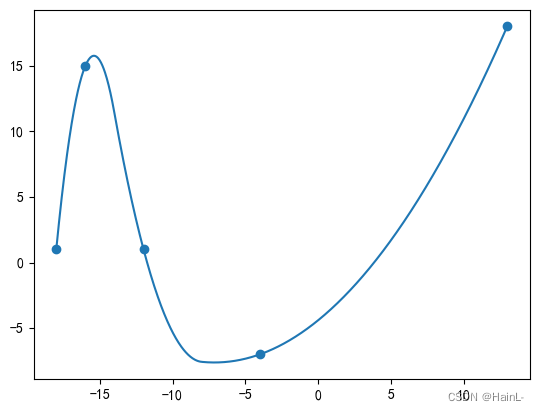
分段插值的特点是插值多项式是连续的,但得到的插值曲线其实是不光滑的,因为插值多项式的导数并不在分段点连续,也就是并不能处处可导,甚至有时在分段点会出现尖刺。
3. Hermite插值
如果想得到连续处处一阶或高阶可导的光滑插值曲线,我们可以考虑分段Hermite插值。
本质是提供插值点的被插值函数的导数数据,同时对函数本身及其导函数进行插值
(1)一重Hermite插值
只须提供函数本身的插值点函数值即可,得到的Hermite插值曲线连续一阶可导
poly31=interpolate.KroghInterpolator(x,y) #一重Hermite插值
plt.plot(xdense,poly31(xdense))
plt.scatter(x,y)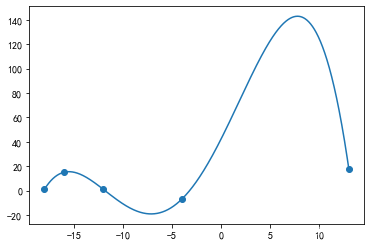
(2)二重Hetmite插值
提供函数和一阶导函数的插值点函数值,得到的Hermite插值曲线连续二阶可导,也就是一阶导数光滑。
通常我们并不知道被插值数据点的导函数值,因此我们可以假设插值点处函数及一阶导函数的数据相同,直接将插值点及其对应的数据复制一份,使输入的数据变成和
。
xdb=np.column_stack([x,x]).reshape(-1)
ydb=np.column_stack([y,y]).reshape(-1)
poly32=interpolate.KroghInterpolator(xdb,ydb) #二重Hermite插值
plt.plot(xdense,poly32(xdense))
plt.scatter(x,y)
4. 样条插值
样条插值的特点是不提供一阶导数的数据,也能得到连续二阶可导,也就是一阶导数光滑的插值曲线。
poly4=interpolate.interp1d(x,y,'cubic') #样条插值
plt.plot(xdense,poly4(xdense))
plt.scatter(x,y)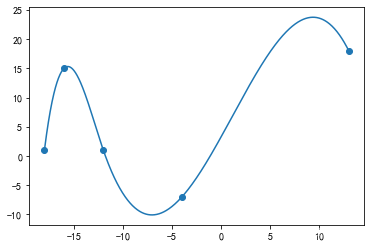























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








