一、傅立叶变换
import numpy as np
import matplotlib.pyplot as plt
from scipy import fftpack1. 离散傅立叶变换(DFT)
将傅立叶变换为
,可通过一个傅立叶矩阵进行变换:
矩阵元为,其中
也就是说,
这一方法的时间复杂度为
2. 快速傅立叶变换(FFT)
在DFT的基础上,注意到当j*k分别为N/2、N、3N/2、2N时,有值的将会依次为
。因此我们可以尝试利用
的周期性:
当将 k 为偶数时,,根据周期性有
因此当 k 为偶数时,有,也就是说第j行与j+N/2行的矩阵元是相同的。
同理,当 k 为奇数时,我们只需要分离出一个的公因数,剩下的部分也满足偶数的条件。
因此,我们只需要将奇偶列分开并各自利用的性质求解,就能极大的加速算法,将时间复杂度由
降为
3. 利用scipy进行傅立叶变换
(1)正变换
x = np.linspace(0,2*np.pi,20000,)
a = 30*np.sin(x) + 20*np.cos(10*x) + 10*np.sin(20*x) + 5*np.cos(30*x)
c = fftpack.fft(a)/len(a) #傅立叶变换,除以len(a)是为了归一化
k = fftpack.fftfreq(len(a)) #傅立叶曲线的频率轴
plt.plot(x,a)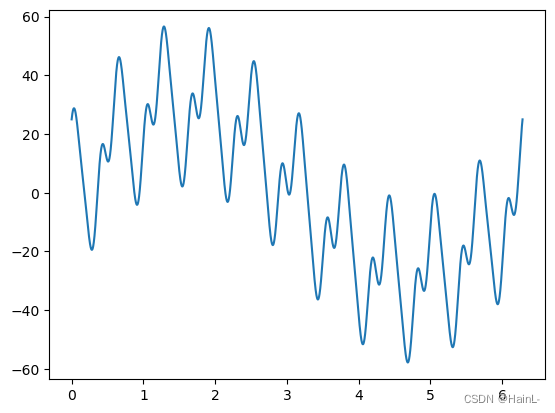
plt.plot(k,abs(c))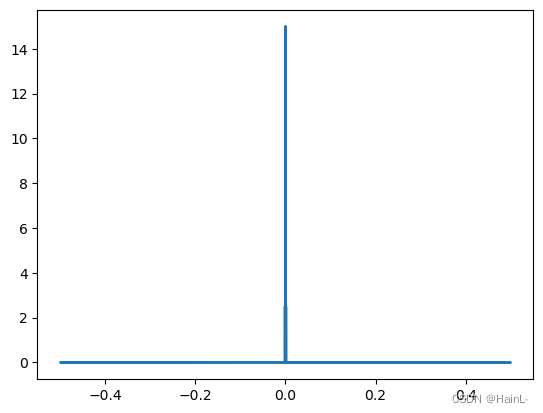
fft函数计算的模数太多,以至于分辨不出图像。示例给出的周期函数用不了那么多模。
plt.plot(k[:50],abs(c)[:50]) #手动选取前50个mode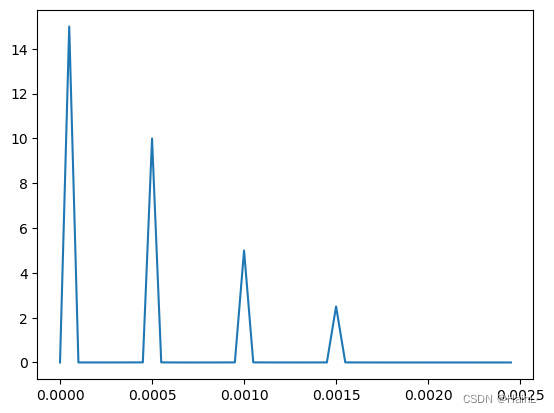























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








