面试杂项3

最新推荐文章于 2023-04-20 07:39:14 发布

夕阳那边

最新推荐文章于 2023-04-20 07:39:14 发布

阅读量2.5k

点赞数

分类专栏：面试

本文链接：https://blog.csdn.net/iihtd/article/details/51707319

版权

面试专栏收录该内容

6 篇文章 0 订阅

订阅专栏

编程题给了一个链表，第1个结点标号为1，把链表中标号在M到N区间的部分反转（我写的很慢，面试官看不下去了，让我只说思路）
我的思路是两个指针，计算出M-N的距离，然后一起出发。
将这段区域中的链表反转，然后再添到原来的链表里面。
**编程题在一个字符串中，找出最长的无重复字符的子串（这个问题还是有难度的，我碰巧想到了用hash，但没想到完整解法，用hash的解法复杂度在O(N^2)，在网上查了下，好像还有更快解法
http://blog.csdn.net/luxiaoxun/article/details/8036544
最长子串
主要是生成next数组和first数组

int hash[N] ;
初始化hash中每个元素都是N，vector<int> hash(num , value);
int next[N] ;
int first [N+1] ;
first[N] = N ;
for (size_t i = N- 1 ; i >= 0 ; i--){
    if(hash[str[i]] == N){ //  这个单词还没有出现过
        next[i] = N;
        first[i] = first[i+1];
    }
    else {
        next[i] = hash[str[i]];
        first[i] = hash[str[i]]; 
    }
    hash[str[i]] = i;
}  
最后统计出fisrt[i] - i 的最小值就可以了。
原因是，first[i]记录的是包括i和i之后的字母重复出现的时候的位置，也就是说[i, first[i] - 1]之间都没有重复的元素，如果相等就是指的i元素本身，他们之间的元素的个数是first[i]-1-i+1

有2个很大的文件，也就是不能放到内存中，文件的每一行存放的是一个URL，每个文件的URL都不重复，但是两个文件之间可能有重复的，让你找出两个文件重复的URL。
他说bitmap中有重复的怎么办，我说如果重复了就可以说明这个URL是重复的，就可以确定了。然后面试官也木有说什么了。**
将两个文件做通过相同的hash函数hash成为num个文件对，相同的url只可能会出现在相同的文件对立面。

如果只能够存数字，可以存MD5
时间复杂度包括划分的时间复杂度和比较的时间复杂度O(文件1单词个数)+O(文件2单词个数)
hash函数可以是

 unsigned int BKDRHash(char *str)
{
    unsigned int seed = 131; // 31 131 1313 13131 131313 etc..
    unsigned int hash = 0;

    while (*str)
    {
        hash = hash * seed + (*str++);
    }

    return (hash & 0x7FFFFFFF);
}

可以谈到boolm过滤器，暴雪hash，还有google的hash等。

**开放问题：
设计一个合理的电梯调度策略，调度两个电梯，考虑满足基本的接送需求，满足能耗最小，满足用户等待时间最短（难到我了，我想的方法不好，面试告诉我了他的想法，类似于一个进程调度问题，每一时刻只可能有一个用户按按钮，把这条指令接收，判断当前电梯能否满足，能满足就执行，不能满足则放入一个队列里，实际情况还要细化）**
饥饿问题

异常情况（为每个电梯都设立一时计时器，任务超时后调用第二台电梯）
如果电梯在自己方向上面没有任务，可以回转
调度最短距距离上面的电梯
倒排索引
链表逆置
strcpy函数的编写？（这个函数很熟悉，后来阿里校招面试也让现场编写了）（常考3）

不考虑第一个dst和src存在交叠的情况下
char * strcpy(char *dst,const char *src)   //[1]
{
    assert(dst != NULL && src != NULL);    //[2]
    if(dst == src ){ 
        return dst;
    }
    char *ret = dst;  //[3]
   // 右边，src先++，但是在用的时候，*src还是原来的值，des也是一样
    while ((*dst++=*src++)!='\0'); //[4]
    return ret;
}
//考虑dst和src存在交叠的情况
size_t my_strlen(char *str){
        size_t len = 0;
        while (*str++ != '\0') {
                len++;
        }
        return len;
}
char *my_memcpy(char *dst, const char* src, int cnt)
{
    assert(dst != NULL && src != NULL);
    if(dst == src){
        return dst;
    }
    char *ret = dst; 
    if (dst = src && dst <= src+cnt-1) //
    {
        dst = dst+cnt-1;
        src = src+cnt-1;
        while (cnt--) //从最后的\0处开始复制
            *dst-- = *src--;
    }
    else    //正常情况，从低地址开始复制
    {
        while (cnt--)
            *dst++ = *src++;
    }    
    return ret;
}
char * strcpy(char *dst,const char *src)
{
    assert(dst != NULL && src != NULL);
    if(dst == src) {
        return dst;
    }       
    char *ret = dst;
    my_memcpy(dst, src, my_strlen(src)+1);
    return ret;
}

不调用C++/C的字符串库函数，请编写函数 strcpy
如何获取一个网站每天的访问用户数（A）

c++：

List接口和Set接口的区别
size，。。。？
有两个线程A和B,如果一个线程要等另一个线程执行完，该怎么做信号量？加锁？
C++智能指针的实现
看自己的博客
vector的分配问题，vector为什么每一次扩容都是2倍
http://www.zhihu.com/question/36538542/answer/67929747

在vector中插入n个数的时间复杂度
如果是在后面插入的话，而且本来时间是够的，那么就是O（n），如果是在前面插入的话O（N*N）
说说C语言中union和const关键字
union：

一个union 只配置一个足够大的空间以来容纳最大长度的数据成员；
在C++里，union 的成员默认属性页为public。union 主要用来压缩空间。如果一些数据不可能在同一时间同时被用到，则可以使用union；
判断大小端

判断大小端
小端：数字的低位，比如说整数的个位，存储在存储这块整数的低地址处，比如说0x00；而c语言中的union是低地址对齐的：

bool IsLittleEnd()//返回1，为小端；反之，为大端；
{
    union
    {
        unsigned int  a;
        unsigned char b;
    }c;
    c.a = 1;
    return 1 == c.b;
}

C程序内存布局

//main.cpp
int a = 0;                      // 全局初始化区(data)
char *p1;                       // 全局未初始化区(bss)
int main()
{
    int b;                      // 栈区(stack)
    char s[] = "abc";           // 栈区(stack)
    char *p2;                   // 栈区(stack)
    char *p3 = "123456";        // p3 在栈区(stack);   "123456\0" 在常量区(rodata)
    static int c =0;            // 全局/静态 初始化区  (data)
    p1 = (char *)malloc(10);
    p2 = (char *)malloc(20);    // 分配得来的 10 和 20 字节的区域就在堆区 (heap)
    strcpy(p1, "123456");       // "123456\0" 放在常量区(rodata). 编译器可能会将它与 p3 所指向的"123456\0"优化成一个地方。
    return 0;
}

程序代码区（.text） - 存放函数体的二进制代码。
文字常量区（.rodata） - 常量字符串就是放在这里的，程序结束后由系统释放(rodata—read only data)。
全局区/静态区（static） - 全局变量和静态变量的存储是放在一块的。初始化的全局变量和静态变量在一块区域(.rwdata or .data)，未初始化的全局变量和未初始化的静态变量在相邻的另一块区域(.bss)，程序结束后由系统释放。
＊在 C++中，已经不再严格区分bss和 data了，它们共享一块内存区域
堆区（heap） - 一般由程序员分配释放(new/malloc/calloc delete/free)，若程序员不释放，程序结束时可能由 OS 回收。
注意：它与数据结构中的堆是两回事，但分配方式倒类似于链表。
栈区（stack） - 由编译器自动分配释放，存放函数的参数值，局部变量的值等。其操作方式类似于数据结构中的栈。
Data
The data area contains global and staticvariables used by the program that are initialized. This segment can be furtherclassified into initialized read-only (rodata) area and initialized read-writearea (rwdata).
BSS
The BSS segment also known as uninitialized datastarts at the end of the data segment and contains all uninitialized globalvariables and static variables that are initialized to zero by default.
Heap
The heap area begins at the end of the BSSsegment and grows to larger addresses from there. The heap area is managed bymalloc/calloc/realloc/new and free/delete, which may use the brk and sbrk system calls to adjust its size. The heaparea is shared by all shared libraries and dynamically loaded modules in aprocess.
Stack
The stack is a LIFO structure, typically locatedin the higher parts of memory. It usually “grows down” with everyregister, immediate value or stack frame being added to it. A stack frameconsists at minimum of a return address
http://blog.csdn.net/duyiwuer2009/article/details/7994091
C语言中变量有几种存储方式。这个学过C语言的应该都知道
trie树
假设一棵树的品均高度是len，建立这棵树的时间复杂度是O(N*len*r)，其中r是树中节点的基的大小,查询一个单词的时间复杂度是O(len)。
后缀树
后缀树是一种数据结构。
比如说给定一长度为n的字符串S=S1S2..Si..Sn，和整数i，1 <= i <= n，子串SiSi+1…Sn便都是字符串S的后缀。
空字符串也是属于后缀的一种。
以字符串S=XMADAMYX为例，它的长度为8，所以S[1..8], S[2..8], … , S[8..8]都算S的后缀，我们一般还把空字串也算成后缀。这样，我们一共有如下后缀。对于后缀S[i..n]，我们说这项后缀起始于i。
以字符串XMADAMYX为例
S[1..8], XMADAMYX，也就是字符串本身，起始位置为1
S[2..8], MADAMYX，起始位置为2
S[3..8], ADAMYX，起始位置为3
S[4..8], DAMYX，起始位置为4
S[5..8], AMYX，起始位置为5
S[6..8], MYX，起始位置为6
S[7..8], YX，起始位置为7
S[8..8], X，起始位置为8
空字串，记为$。
而后缀树，就是把单词所有的后缀存在了一个tire树中。如下图所示：

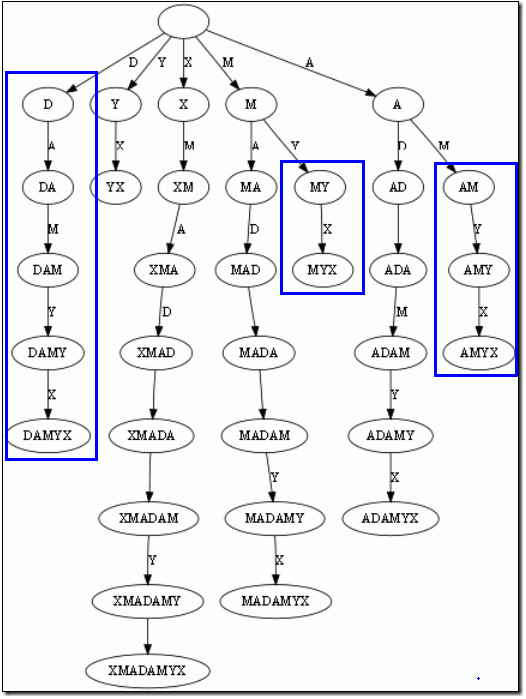
树的压缩：
蓝框标注的分支都是独苗，没有必要用单独的节点同边表示。我们只需要在叶节点上标注上每项后缀的起始位置。于是我们得到下图：
注意标号有点重叠了：

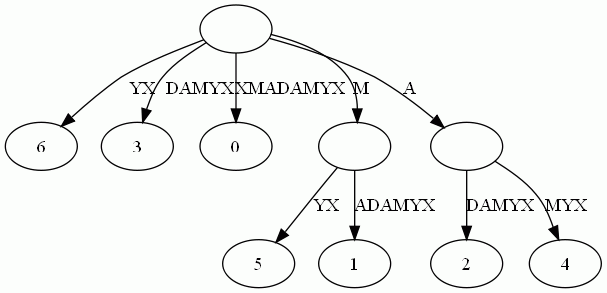
这样的结构丢失了某些后缀。比如后缀X在上图中消失了，因为它正好是字符串XMADAMYX的前缀。解决方案：在待处理的子串后加一个空字符就行了。例如我们处理XMADAMYX前，先把XMADAMYX变为 XMADAMYX$，于是就得到suffix tree–后缀树了，如下图所示，这样每个后缀后面都有一个空字符，后缀就不可能成为某个后缀的前缀了。

至此，后缀树建立完毕。
最长回文
参考文章：https://segmentfault.com/a/1190000003914228
为了统一基数和偶数的处理方式，将每个数字之间都插入#，

aba  ———>  #a#b#a#
abba ———>  #a#b#b#a#

采用RL数组来记录以下标i为中心的回文半径

char:    # a # b # a #
 RL :    1 2 1 4 1 2 1
RL-1:    0 1 0 3 0 1 0
  i :    0 1 2 3 4 5 6

char:    # a # b # b # a #
 RL :    1 2 1 2 5 2 1 2 1
RL-1:    0 1 0 1 4 1 0 1 0
  i :    0 1 2 3 4 5 6 7 8

RL-1，就是原始字符串中以字母i为中心的最大回文长度。
构建RL数组的方法：
辅助变量MaxRight，表示当前访问到的所有回文子串，所能触及的最右一个字符的位置。另外还要记录下MaxRight对应的回文串的对称轴所在的位置，记为pos，它们的位置关系如下。这都是两个变量。
这里写图片描述
从左往右地访问字符串来求RL，现在求RL[i] , i必然是在po右边的。那么现在只需要分情况讨论i是在MaxRigh的左边还是右边的情况。
1）当i在MaxRight的左边

图中两个红色块（包括红色块）的串是回文的；并且以i为对称轴的回文串，是与红色块间的回文串有所重叠的。我们找到i关于pos的对称位置j，这个j对应的RL[j]我们是已经算过的。根据回文串的对称性，以i为对称轴的回文串和以j为对称轴的回文串，有一部分是相同的。这里又有两种细分的情况。

以j为对称轴的回文串比较短，短到像下图这样

这时我们知道RL[i]至少不会小于RL[j]（因为RL[i]还可以向两端扩张），并且已经知道了部分的以i为中心的回文串，于是可以令RL[i]=RL[j]。但是以i为对称轴的回文串可能实际上更长，因此我们试着以i为对称轴，继续往左右两边扩展，直到左右两边字符不同，或者到达边界。

以j为对称轴的回文串很长，这么长：

这时，我们只能确定，两条蓝线之间的部分（即不超过MaxRight的部分）是回文的（PS：有点画过了），于是从这个长度开始，尝试以i为中心向左右两边扩展，直到左右两边字符不同，或者到达边界。

不论以上哪种情况，之后都要尝试更新MaxRight和pos，因为有可能得到更大的MaxRight。如果更新了，那么就是现在的MaxRight和pos。
2）当i在MaxRight的右边
这里写图片描述

遇到这种情况，说明以i为对称轴的回文串还没有任何一个部分被访问过，于是只能从i的左右两边开始尝试扩展了，当左右两边字符不同，或者到达字符串边界时停止。
然后更新MaxRight和pos。
算法实现：

#Python
def manacher(s):
    #预处理
    s='#'+'#'.join(s)+'#'

    RL=[0]*len(s)
    MaxRight=0
    pos=0
    MaxLen=0
    for i in range(len(s)):
        if i<MaxRight:
            RL[i]=min(RL[2*pos-i], MaxRight-i)
        else:
            RL[i]=1
        #尝试扩展，注意处理边界
        while i-RL[i]>=0 and i+RL[i]<len(s) and s[i-RL[i]]==s[i+RL[i]]:
            RL[i]+=1
        #更新MaxRight,pos
        if RL[i]+i-1>MaxRight:
            MaxRight=RL[i]+i-1
            pos=i
        #更新最长回文串的长度
        MaxLen=max(MaxLen, RL[i])
    return MaxLen-1

C语言版本的
将str中插入#符号；
定义RL数组；
定义变量MaxRight、po，MaxLen；
for（i : N）{
    //初始化RL变量
    if(i < MaxRight){
        //RL取j对应的边界和MaxRight对应的边界的最小值，因为只有这个范围里面才能够保证RL[i]范围里面是回文的；
        RL[i] = min(RL[2*pos - i ] ,MaxRight -1 );
    }
    else {
    //从RL[i]本身开始向两边扩张
        RL[i] =1 ;
    }
    //尝试扩展，注意处理边界
    while (i-RL[i]>=0 && i+RL[i]<len(s) && s[i-RL[i]]==s[i+RL[i]]{
            RL[i]+=1;
    }
    //更新MaxRight和pos
    if (RL[i]+i-1>MaxRight){
            MaxRight=RL[i]+i-1 ;
            pos=i ;
     }
     //更新最长回文串的长度
     MaxLen=max(MaxLen, RL[i]);
     return MaxLen-1;
}

复杂度分析：
空间复杂度：插入分隔符形成新串，占用了线性的空间大小；RL数组也占用线性大小的空间，因此空间复杂度是线性的。
时间复杂度：尽管代码里面有两层循环，通过amortized analysis我们可以得出，Manacher的时间复杂度是线性的。由于内层的循环只对尚未匹配的部分进行，因此对于每一个字符而言，只会进行一次，因此时间复杂度是O(n)。