【数据结构】6.6 赫夫曼树及其应用

最新推荐文章于 2023-05-13 16:00:02 发布

致命小学期

最新推荐文章于 2023-05-13 16:00:02 发布

阅读量929

点赞数

分类专栏：数据结构文章标签：数据结构 c++

本文链接：https://blog.csdn.net/iivan_cpp/article/details/121457180

版权

数据结构专栏收录该内容

9 篇文章 2 订阅

订阅专栏

例4：假设二叉树T中至多有一个结点的数据域值为x,试编写算法拆去以该结点为根的子树，使原树中分成两棵子树。

6.6.1、最优二叉树(赫夫曼树)

1、几个概念

树的路径长度：从根结点到所有结点的路径长度之和；

结点的带权路径长度：结点到根结点的长度与权重的乘积；

路径长度：路径上边（分支）的个数；

树的带权路径长度：所有叶结点的带权路径长度之和。

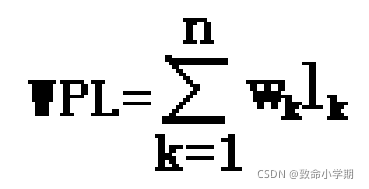
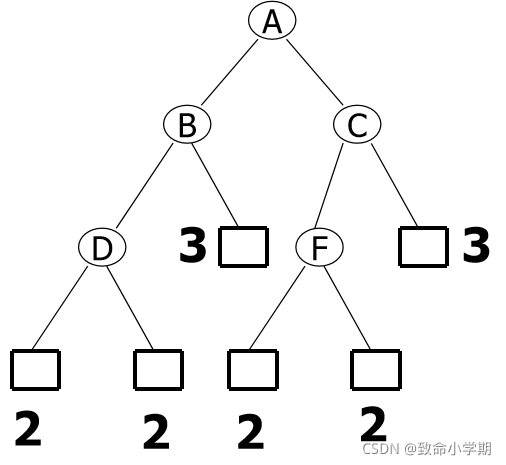
3×2+3×2+2×3+3×2+3×2+2×3=36

2、赫夫曼树(最优二叉树)：是具有最小带权路径长度的二叉树。

.构造赫夫曼树(赫夫曼算法)

(1)构造赫夫曼树的基本思想

假设由权值分别为w1，w2 ， … ， wn的 n个叶子结点组成一棵二叉树。要想使WPL

值最小，必须使权值大的叶子结点尽量靠近 根结点，而使权值小的叶子结点尽量远离根

结点。

(2)构造赫夫曼树的例子

n个叶结点，按上述构造方法，树中共有多少个结点？

2n-1个

(3)构造赫夫曼树的算法

a. 给定的n个权值{w1,w2,……,wn}构成具有n棵二叉树的森林F={T1，T2，……,Tn}，其中每棵二叉树Ti只有一个 权为wi的结点(根结点，无左右子树)。

b.在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为 其左、右子树上根结点的权值之和。

c.在集合F中删除先前所选取的两棵二叉树，并把新构成的二叉树加入到F中；

d.重复执行b，c两步，直到F中只剩下一棵二叉树。

(4)构造赫夫曼树的一种存储结构和生成过程

6.6.2、赫夫曼编码

1.问题的提出

(1)编码的长短（等长编码）

在英文通信中，计算机经常需要将字符转化为二进制编 码。

例：设电文中只用了A,B,C,D四个字母；

采用二位编码为00，01，10，11；

电文为“ACDACAB”的二进制代码串：00101100100001；

总长14位，对方接收后可按每二位对照字符进行译码。

(2)不等长编码：

在实际应用中，由于字符出现的频率不同，可采用不 等长编码降低编码的长度；

在“ACDACAB”中A，C出现的次数较多，A,C编码要

短：例如0(A),00(B),1(C),01(D)，电文的二进制代码串：

010101000，总长为9位。

(3)译码唯一性

采用不等长编码出现的问题，译码唯一性。

采用不等长编码，要保证译码唯一性，必须采用前缀编码。

(4)前缀编码。

要求任一个字符的编码都不是另一个字符的编码的前缀，这种编码称做前缀编码。

A,B,C,D的编码为：0， 00，1， 01

A,B,C,D的编码为：00，01，10， 11

A,B,C,D的编码为：0， 10，110，111

2.电文长度与哈夫曼树。

假设组成电文的字符集合是D = { d1, d2, ... dn }, 每个字符出现的次数是c1, c2, ..., cn, di对应的

编码长度是li。

通常我们用di出现的概率来代替出现的次数，

设di出现的概率为wi。

(1)赫夫曼编码举例

利用赫夫曼树对句子“it is a tree”进行编码。

句子中有字符：{i，t，□，s，a，r，e}共七个字符。

七个字符的权值分别为：{2，2，3，1，1，1，2}。

编码过程

见图

编码结果：

i t □ i s □ a □ t r e e

011 10 11 011 001 11 0000 11 10 0001 010 010

赫夫曼编码——利用赫夫曼树得到的前缀编码。

(2)赫夫曼编码的方法

a. 首先构造出赫夫曼树：

b. 设计赫夫曼编码：在有了赫夫曼树之后， 将树中每个结点的左分支用“0”代表，右分支用

“1”代表。则从根结点到叶结点之间，沿途路径 上的分支组成的“0”或“1”代码串就是该叶子结

点所代表的字符编码，称为赫夫曼编码。

(3)赫夫曼编码的特点

由赫夫曼树的构成可知权大的结点靠近根结点，其路径短。

电文的总长度最短。

赫夫曼树是带权路径长度最短的二叉树。

前缀码

赫夫曼编码对应终点为叶子的路径，相互不完全重叠。

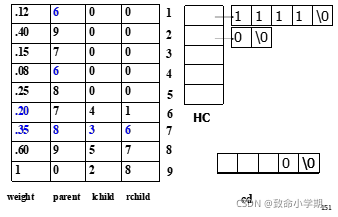
1号

1号是6号的右孩子，1号哈夫曼编码的最后一位是1

再找6号的父节点是7号

6号是7号的右孩子，倒数第二位是1

再找7号的父节点是8号

7号是8号的右孩子，倒数第3位是1

再找8号的父节点是9号

8号是9号的右孩子，倒数第4位是1

再找9号的父节点是0号根节点

终止

临时存储空间1111 \0

根据长度申请存储空间

字符指针数组指向每一个编码

赫夫曼树和赫夫曼编码的存储表示

typedef struct
{
    unsigned int weight;//权重 
    unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree;

typedef char**HuffmanCode;

//树，编码，权重数组 ，叶子结点个数
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,float *w,int n)//
{
    //构造哈夫曼树
    if(n<=1 )return;
    m = 2*n-1; //树的结点个数
    //0号空间不用 从1开始 
    HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));//存储空间
	//初始化 叶子结点 
	for(p=HT,i=1 ; i<=n;i++,p++,w++)
	{
		*p={*w,0,0,0};//赋值 权重消息 父节点和左右孩子位置赋值为0 
	} 
	//
	for( ;i<=m;i++,p++) 
	{
		*p={0,0,0,0};
	}
	//构造哈夫曼树
	for(i=n+1;i<=m;i++)
	{
		//选择的时候会把父节点考虑进去 所以结果正确 
		select(HT,i-1,s1,s2);//从1到i-1 也就是之前的结点中找两个最小值位置
		HT[s1].parent=i;
		HT[s2].parent=i;
		HT[i].lchild=s1;
		HT[i].rchild=s2;
		HT[i].weight=HT[s1].weight+HT[s2].weight; 
	}//生成哈夫曼树
	
	///哈夫曼编码
	HC=(HuffmanCode)malloc((n+1)*sizeof(char*));//0号不用
	cd=(char*)malloc(n*sizeof(char));
	//临时，存放每一次叶子结点的哈夫曼编码的n-1位+最后的'\0' 
	cd[n-1]='\0';//编码结束符
	for(i=1;i<=n;i++)//前n个结点
	{
		start=n-1;//反着求，开始是n-1，编码结束符位置
		for(c=i,f=HT[i].parent ; f!=0 ; c=f,f=HT[f].parent )
		{//直到找到根节点 
			if(HT[f].lchild==c)//左孩子为0
				cd[--start]='0';
			else
				cd[--start]='1'; 
		} 
		HC[i]=(char*)malloc((n-start)*sizeof(char));
		strcpy(HC[i] , &cd[start] );
	}
	free(cd);//释放临时工作空间 
}//HuffmanCoding

void select(HuffmanTree &HT,int pos,int &s1,int &s2)
{
	int min;
	int i;
	for(i=1;i<=pos;i++)//找第一个基准值 
	{
		if(HT[i].parent==0)
		//从parent为0也就是没有被选过得结点中选一个开始比较 
		{
			min=i;//
			break;
		}
	}
	for(int i=1;i<=pos;i++)
	{
		if(HT[i].parent==0)//未选择
		{
			if(HT[i].weight < HT[min].weight )
			{
				min=i;
			}
		 } 
	} 
	s1=min;
	//第二个最小值
	for(int i=1;i<=pos;i++)
	{
		if(HT[i].parent==0 && i !=s1)
		{
			min=i;
			break;
		}
	} 
	for(int i=1;i<=pos;i++)
	{
		if(HT[i].parent==0 && i!=s1)
		{
			if(HT[i].weight < HT[min].weight )
				min=i;
		}
	}
	s2=min;
}

对同一段电文进行哈夫曼编码，下面哪个表述是正确的？

构造的哈夫曼树是一样的。 （可以作为左右子树，权值一样的结点）

构造的哈夫曼树可能不同，但同一个字符哈夫曼编码是 一样的。

构造的哈夫曼树可能不同，但同一个字符的编码长度是 一样的。

总的字符编码长度是一样的。

例4：假设二叉树T中至多有一个结点的数据域值为x,试编写算法拆去以该结点为根的子树，使原树中分成两棵子树。

例题例题

采用前序递归算法：

1、如果t->lchild->data==x; //t的左孩子是x

p=t->lchild;t->lchild=null;

返回p;

如果t->rchild->data==x;

p=t->rchild;t->rchild=null;

返回p;

2、否则在左子树中查找；

3、如果在左子树中没有找到，则在右子树中查找。

4、如果树中没等于x的结点，返回空值。

Bitree p=NULL;//全局变量；新树的根结点。

void dissect(Bitree t,int x)

{

if(t!=NULL && t->lchild!=NULL ) //有左孩子

{

if(t->lchild->data==x) //找到结点

{

p=t->lchild;

t->lchild=NULL;

}

else if(t!=NULL && t->rchild!=NULL ) //有右孩子

{

if(t->rchild->data==x)

{

p=t->rchild;

t->rchild=NULL;

}

if(t!=NULL && !p) dissect(t->lchild,x); //左子树中查找

if(t!=NULL && !p) dissect(t->rchild,x); //右子树中查找

}

致命小学期

关注

0
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
【数据结构】6.6 赫夫曼树及其应用

6.6.1、最优二叉树(赫夫曼树)1、几个概念树的路径长度：从根结点到所有结点的路径长度之和；结点的带权路径长度：结点到根结点的长度与权重的乘积；路径长度：路径上边（分支）的个数；树的带权路径长度：所有叶结点的带权路径长度之和。3×2+3×2+2×3+3×2+3×2+2×3=362、赫夫曼树(最优二叉树)：是具有最小带权路径长度的二叉树。.构造赫夫曼树(赫夫曼算法) (1)构造赫夫曼树的基本思想假设由权值分别为w1，w2 ， … ，...
复制链接

扫一扫