文章目录
一:什么是红黑树
红黑树是AVL树的一种流行变种,是具有以下五个特点的二叉查找树:
- 每一个节点或者着成红色,或者着成黑色
- 根是黑色
- 每个叶节点Nil是黑色
- 如果一个节点是红色的,那么它的子节点必须是黑色的
- 每一条从某节点到某Nil指针的路径必须包含相同数目的黑色节点

二:关于红黑树的一般操作
对红黑树操作,最困难的就是保持上述的红黑树性质中的红色标记部分。
1.查找操作
红黑树是二叉查找树,所以其查找操作与一般的二叉查找树相同
- 令根节点为当前节点
- 当前节点为Nil,返回Nil
- 要找的值等于当前节点,返回当前节点
- 要找的值大于当前节点, 令右儿子为当前节点,重复步骤2
- 要找的值小于当前节点,令左儿子为当前节点,重复步骤2
操作的时间复杂度O(logN)

2. 插入操作
当我们想向树中插入一个新节点时,通常把这个节点作为叶节点插入。
Part1:
假设把这个点涂成黑色,那完了,肯定违反了条件5,因为本来任意的节点到某Nil指针的路径中黑色节点数是相同的,现在加上黑色节点的这条路径黑色节点数度肯定会+1,于是原来的条件被破坏了,因此,新加的节点必须被涂成红色。
Part2:
如果新插入的节点的父节点是黑色的,那么直接插入新的红节点就完事了
Part3:
如果新插入的节点的父节点是红色,那么条件4就被破坏了,这种情况下,我们必须在保持条件5不被破坏的同时,利用改变节点颜色以及树的旋转来满足所有条件。
2.1 新节点:我是红色的,我爹是红色的,我叔叔是黑色的
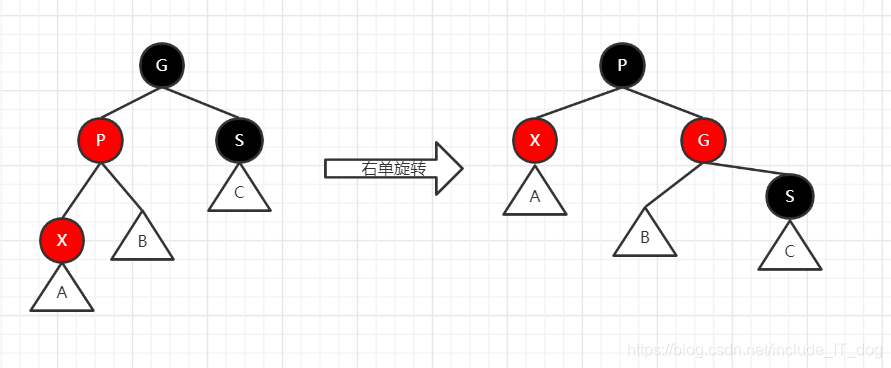
- 设置P为黑色
- 设置G为红色
- 进行右单旋转
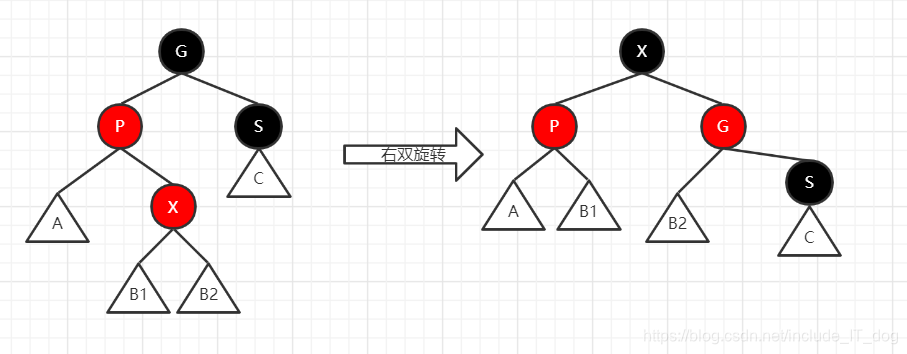
- 设置X为黑色
- 设置G为红色
- 进行右双旋转
还有对称的两种情况,操作也是对称的
2.2 新节点:我是红色的,我爹是红色的,我叔叔也是红色的
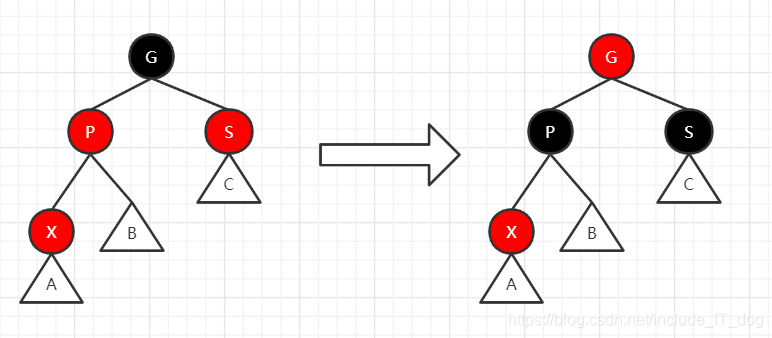
- 把G节点设置为红色
- 把P节点设置为黑色
- 把S节点设置为黑色
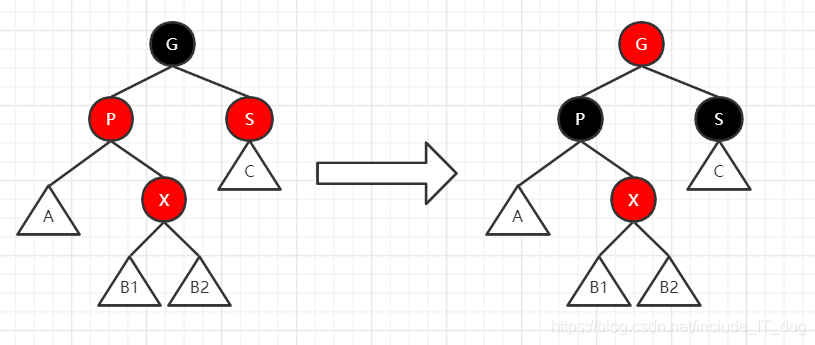
- 把G节点设置为红色
- 把P节点设置为黑色
- 把S节点设置为黑色
这时候,如果G的父节点也是红的,那么G的颜色翻转的操作就会影响性质4,于是我们对G节点以及其父节点GP和父节点的兄弟节点GPS进行2.1所示的旋转操作。
注意如果G的父节点GP为红色,G父节点的兄弟节点GPS肯定不能为红色,只能为黑色,因为在红黑树中,不可能出现出现深度小于树的总深度且双兄弟都为红的情况,这种情况在其他的插入或删除过程中已经消除了。
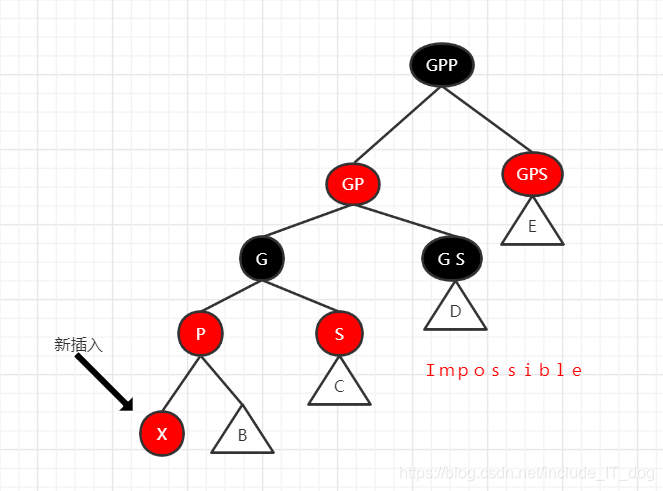
GP刚好为根结点时,那么根据性质2,我们必须把GP重新设为黑色,那么树的红黑结构变为:黑黑红。换句话说,从根结点到叶子结点的路径中,黑色结点增加了。这也是唯一一种会增加红黑树黑色结点层数的插入情景。
还有对称的两种情况,操作也是对称的
伪代码
RB-INSERT(T, z)
//红黑树插入
y = T.nil
x = T.root
while x != T.nil
y = x
if z.key<x.key
x = x.left
else x = x.right
z.p = y
if y == T.nil
T.root = z
else if z.key < y.key
y.left = z
else y.right = z
z.left = T.nil
z.right = T.nil
z.color = RED
//对红黑树的性质进行恢复
RB-INSERT-FIXUP(T, z)
RB-INSERT-FIXUP(T, z)
//插入红色子节点,破坏了性质4时
while z.p.color = RED
//父节点为左子树
if z.p == z.p.p.left
//获取叔叔结点y
y = z.p.p.right
//叔叔结点为红色
if y.color = RED
z.p.color = BLACK
y.color = BLACK
z.p.p.color = RED
z = z.p.p
//叔叔结点为黑色
else
//新插入的结点为父节点的右孩子,先来个父子调换,先进行一次左旋转
if z == z.p.right
z = z.p
LEFT-ROTATE(T,z)
//化成了叔叔结点黑色的一般情况
z.p.color = BLACK
z.p.p.color = RED
RIGHT-ROTATE(T, z.p.p)
//对称情况
else (same as then clause with "right" and "left" exchanged)
T.root.color = BLACK
难点来了,难点来了!!

其实不难
3.删除操作
删除操作一直一来是树这种ADT的难点所在
一般二叉搜索树的删除操作:
- 该节点为叶节点的情况:可以直接删除,将其父节点的儿子指针设为Nil
- 该节点只有一个非空子节点:可以直接删除,将其父节点的儿子指针指向其唯一儿子
- 该节点有两个非空子节点:用该节点左子树的最大节点或者右子树的最小节点替换该节点,然后删除对应的左子树最大节点或者右子树最小节点,最终可以回到前两种情况。
好,到这里你肯定还是明白的对吧

现在考虑红黑树的删除操作。
注意:
根据一般二叉搜索树的删除操作来看,我们要删除的节点其实不一定是最终从图中移出去的节点,称最终从图中移出去的节点为替代点,我们先从右子树的最小节点(或左子树的最大节点)找到我们的替代点,与删除点的值交换,但是颜色都不变,然后再删除替代点,然后对树的性质进行恢复。而现在这些替代点都是一些树的末节点(区别于叶节点,我们现在将Nil节点视为黑色叶节点),删除操作便会简化许多,并可以归纳为像插入那样的几个类别。当然了替代点和我们要删除的点也有可能是同一点,但处理方法是一样的。
我们虽然删除了替代点,但是我们对树进行恢复时,还是会将该替代点放在树中参与恢复,恢复完成后再移掉。
在本文中,示例都默认是选择右子树的最小节点作为真正删除点,也可以选择左子树的最大节点
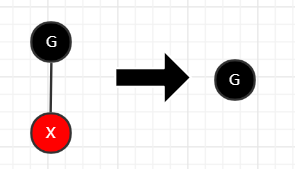
3.1替代点是红色的
直接从树中去掉即可,不会影响红黑树的性质,算法直接结束
不会出现替代点为红色且有儿子为非叶子节点的情况,所以这种情况是最简单的
3.2替代点是黑色的
替代点是黑色,那么删除之后树的性质就被破坏了,需要进行修复
3.2.1 有一个儿子为且必须为红色时
当替代节点只有一个儿子且为红色时
直接用它的红色儿子节点取代它,并将颜色改为黑色,这样所有经过替代节点的路径都将经过他的儿子,黑色高度不变。
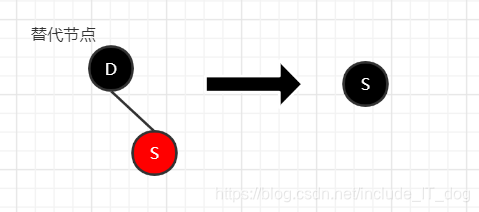
注意这跟上面图不一样,这张图D节点是替代节点
不可能存在只有一个儿子且儿子为黑色的情况,那样本身就是不平衡的
3.2.2 有两个黑色儿子
当替代点是黑色的且有两个黑色儿子(可以为叶节点Nil)时,那他肯定有兄弟,那么又可以分为其他几类
- 替代点是黑色,其兄弟节点是红色
- 替代点是黑色,其兄弟节点是黑色
3.2.2.1 替代点的兄弟节点是红色
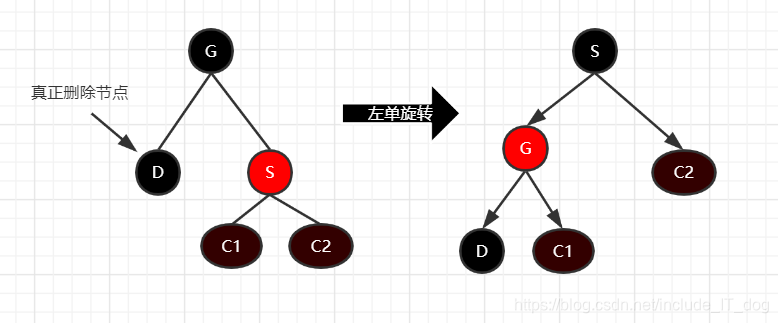
- 将G节点也就是替代点的父节点设置为红色,
- 兄弟节点S设置为黑色
- 然后进行向左单旋转,
现在可以直接删掉D了吗?(以下都默认标识D为替代点) 不 行 , t a n 90 ° \hspace4ex 不行,tan90\degree 不行,tan90°
这个操作不改变任何路径的黑色高度,这时候删去D肯定会变的不平衡,我们只是把情况变为了兄弟节点为黑色的情况,也就是下面将要叙述的情况,我们接下来需要重新进入算法,进一步处理
3.2.2.2 替代点的兄弟节点是黑色
替代点D与其兄弟节点S都是黑色的,所以D的父节点颜色是不确定的,用绿色表示
又分为以下几种情况
3.2.2.2.1 当兄弟节点的两个儿子也都是黑色
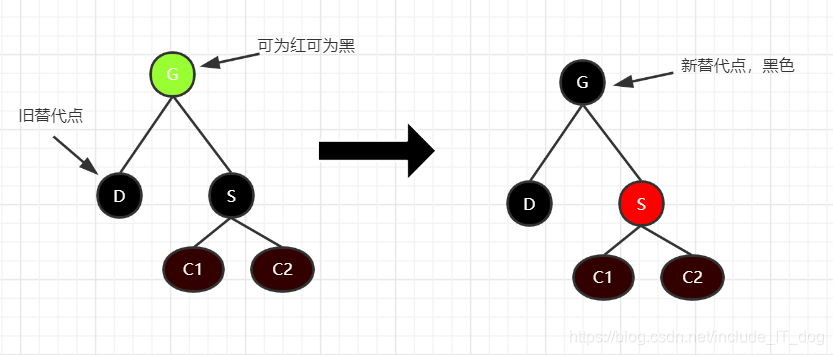
PS:C1、C2可为Nil
- S节点颜色变为红
- G节点颜色变黑
- 把G作为新的替代点进行下一轮操作
假设G一开始是黑色的,这个操作过后,所有一开始经过S节点的路径黑色高度-1,那么在删除D节点后,所有经过D节点的路径黑色高度也会-1,这棵子树大家黑色高度都减一,结局竟该死的甜美,但是经过G的比不经过G的黑色高度减一了,所以再在G上重新平衡处理
假设G一开始是红色的,这个操作后,所有一开始经过S节点的路径黑色高度不变,经过D的路径黑色高度+1,那么在删除D后,所有经过D节点的路径黑色高度又变回来了,结局竟还是该死的甜美,经过G为根的子树已经平衡了,再在G上重新平衡处理
注意当G是树的根时,就表示我们已经做完了,我们从所有路径去除了一个黑色节点,所有性质在上溯过程中都保持着。
3.2.2.2.2 当兄弟节点的左儿子是红色的,右儿子是黑色
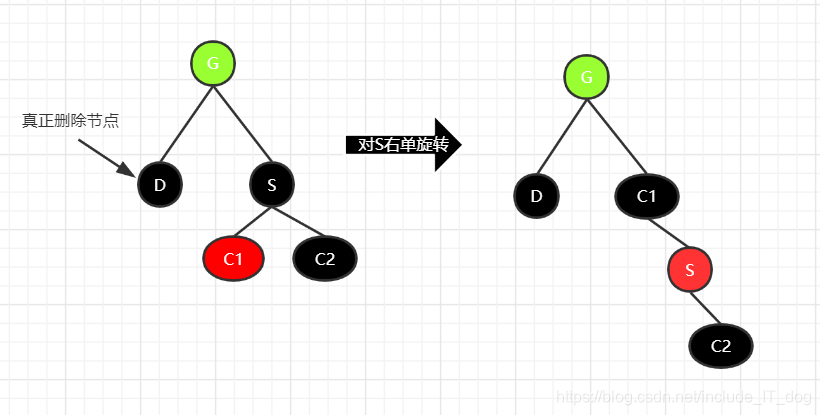
- C1设置为黑色
- S设置为红色
- 对S进行向右单旋转
这样的操作不改变任何路径的黑色高度,本来的平衡状态不变,所以删除D之后就破坏了原先的条件,还要进行自平衡变换,此时成了下面一种情况继续处理
3.2.2.2.3 当兄弟节点的右儿子是红色的,左儿子随意
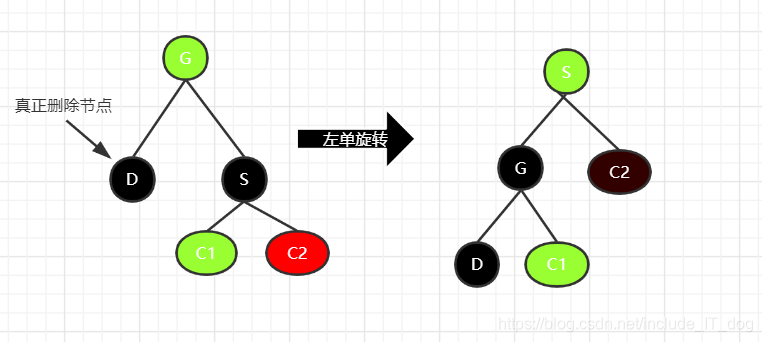
- 交换G和S的颜色
- 设置兄弟节点的右儿子C2为黑色
- 进行向左单旋转
该操作使所有变化前经过S节点的路径黑色高度都不变,经过D的路径黑色高度+1,在删除D后,所有经过G节点的路径都不变,达到平衡
说白了删除就是不断递归变换直到满足替代点的删除条件。
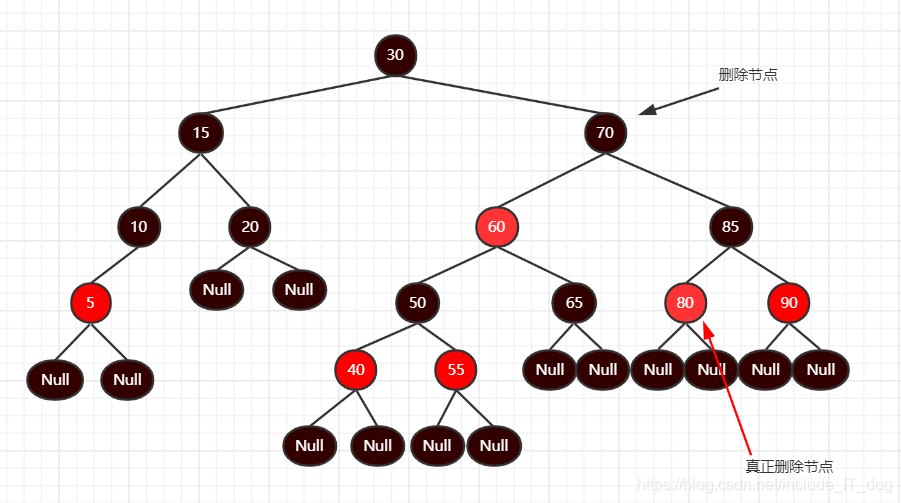
例子:删除30根节点

三:渐进边界的证明
包含n个内部节点的红黑树的高度是 O ( l o g n ) O(logn) O(logn)
定义:
h
(
v
)
表
示
以
节
点
v
为
根
的
子
树
的
高
度
。
{\displaystyle h(v)}表示以节点{\displaystyle v}为根的子树的高度。
h(v)表示以节点v为根的子树的高度。
b
h
(
v
)
表
示
从
v
到
子
树
中
任
何
叶
子
的
黑
色
节
点
的
数
目
{\displaystyle bh(v)}表示从{\displaystyle v}到子树中任何叶子的黑色节点的数目
bh(v)表示从v到子树中任何叶子的黑色节点的数目
(
如
果
v
是
黑
色
则
不
计
数
它
,
也
叫
做
黑
色
高
度
)
。
(如果{\displaystyle v}是黑色则不计数它,也叫做黑色高度)。
(如果v是黑色则不计数它,也叫做黑色高度)。
引
理
:
以
节
点
v
为
根
的
子
树
有
至
少
2
b
h
(
v
)
−
1
个
内
部
节
点
。
引理:以节点{\displaystyle v}为根的子树有至少2^{bh(v)}-1个内部节点。
引理:以节点v为根的子树有至少2bh(v)−1个内部节点。
引
理
的
证
明
(
通
过
归
纳
高
度
)
:
引理的证明(通过归纳高度):
引理的证明(通过归纳高度):
归
纳
假
设
:
归纳假设:
归纳假设:
如
果
v
的
高
度
是
零
则
它
必
定
是
N
I
L
,
因
此
b
h
(
v
)
=
0
b
h
(
v
)
=
0
。
所
以
:
2
b
h
(
v
)
−
1
=
2
0
−
1
=
0
如果v的高度是零则它必定是NIL,因此{\displaystyle bh(v)=0}{\displaystyle bh(v)=0}。所以:2^{{bh(v)}}-1=2^{{0}}-1=0
如果v的高度是零则它必定是NIL,因此bh(v)=0bh(v)=0。所以:2bh(v)−1=20−1=0
如
果
h
(
v
)
=
k
,
有
2
b
h
(
v
)
−
1
个
内
部
节
点
成
立
如果h(v)=k,有2^{bh(v)}-1个内部节点成立
如果h(v)=k,有2bh(v)−1个内部节点成立
于
是
h
(
v
′
)
=
k
+
1
于是h(v')=k+1
于是h(v′)=k+1
因
为
v
′
有
h
(
v
′
)
>
0
所
以
它
是
个
内
部
节
点
。
同
样
的
它
有
的
两
个
儿
子
,
其
黑
色
高
度
要
么
是
b
h
(
v
′
)
要
么
是
b
h
(
v
′
)
−
1
(
依
据
v
′
是
红
色
还
是
黑
色
)
。
通
过
归
纳
假
设
每
个
儿
子
都
有
至
少
2
b
h
(
v
′
)
−
1
−
1
个
内
部
接
点
,
所
以
v
′
有
:
因为v'有h(v')>0 \\所以它是个内部节点。同样的它有的两个儿子,其黑色高度要么是bh(v')要么是bh(v')-1(依据v'是红色还是黑色)。通过归纳假设每个儿子都有至少2^{{bh(v')-1}}-1个内部接点,所以v'有:
因为v′有h(v′)>0所以它是个内部节点。同样的它有的两个儿子,其黑色高度要么是bh(v′)要么是bh(v′)−1(依据v′是红色还是黑色)。通过归纳假设每个儿子都有至少2bh(v′)−1−1个内部接点,所以v′有:
2
b
h
(
v
′
)
−
1
−
1
+
2
b
h
(
v
′
)
−
1
−
1
+
1
=
2
b
h
(
v
′
)
−
1
个
内
部
节
点
。
2^{bh(v')-1}-1+2^{bh(v')-1}-1+1=2^{bh(v')}-1个内部节点。
2bh(v′)−1−1+2bh(v′)−1−1+1=2bh(v′)−1个内部节点。
使 用 这 个 引 理 我 们 现 在 可 以 展 示 出 树 的 高 度 是 对 数 性 的 。 因 为 在 从 根 到 叶 子 的 任 何 路 径 上 至 少 有 一 半 的 节 点 是 黑 色 ( 根 据 红 黑 树 性 质 4 ) , 根 的 黑 色 高 度 至 少 是 h ( r o o t ) 2 通 过 引 理 我 们 得 到 : 使用这个引理我们现在可以展示出树的高度是对数性的。\\ 因为在从根到叶子的任何路径上至少有一半的节点是黑色(根据红黑树性质4),\\根的黑色高度至少是 {\frac {h(root)}{2}}通过引理我们得到: 使用这个引理我们现在可以展示出树的高度是对数性的。因为在从根到叶子的任何路径上至少有一半的节点是黑色(根据红黑树性质4),根的黑色高度至少是2h(root)通过引理我们得到:
n ⩾ 2 h ( r o o t ) 2 − 1 ↔ log ( n + 1 ) ⩾ h ( r o o t ) 2 ↔ h ( r o o t ) ⩽ 2 log ( n + 1 ) n ⩾ 2 h ( r o o t ) 2 − 1 ↔ log ( n + 1 ) ⩾ h ( r o o t ) 2 ↔ h ( r o o t ) ⩽ 2 log ( n + 1 ) {\displaystyle n\geqslant 2^{\frac {h(root)}{2}}-1\leftrightarrow \;\log {(n+1)}\geqslant {\frac {h(root)}{2}}\leftrightarrow \;h(root)\leqslant 2\log {(n+1)}}n\geqslant 2^{{{\frac {h(root)}{2}}}}-1\leftrightarrow \;\log {(n+1)}\geqslant {\frac {h(root)}{2}}\leftrightarrow \;h(root)\leqslant 2\log {(n+1)} n⩾22h(root)−1↔log(n+1)⩾2h(root)↔h(root)⩽2log(n+1)n⩾22h(root)−1↔log(n+1)⩾2h(root)↔h(root)⩽2log(n+1)
因 此 根 的 高 度 是 O ( log n ) 因此根的高度是{\displaystyle {\text{O}}(\log n)} 因此根的高度是O(logn)
























 1398
1398











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










