算法通关村——透彻理解二叉搜索树的应用

本节我们介绍两道有挑战的问题，一道是关于二叉搜索树的，一道是从两个数组中寻找中位数的（也与二分搜索相关）。

有序数组转为二叉搜索树

LeetCode108 给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例1：
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案。

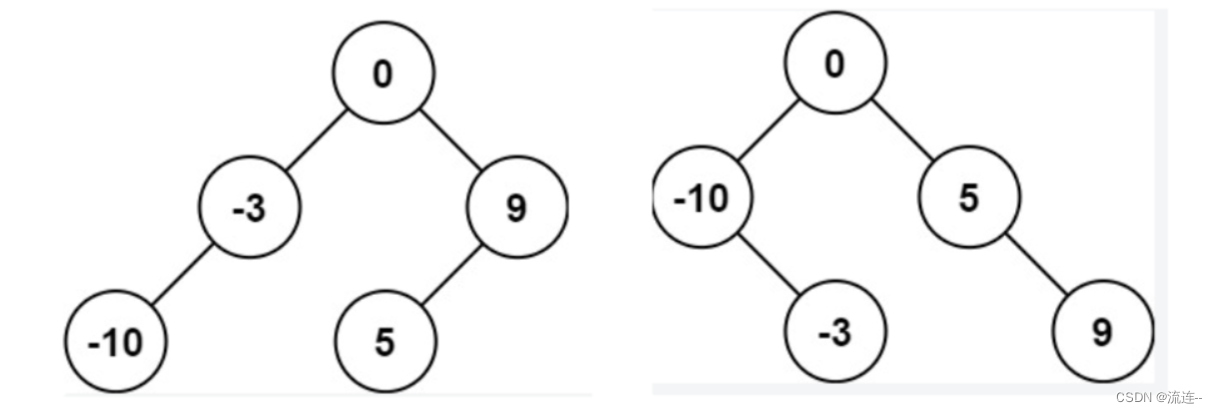
理论上我们要构造二叉搜索树，可以以升序序列中的任意一个元素作为根节点，以该元素左边的升序序列构造左子树，以该元素右边的升序序列构造右子树即可。但是本题要求该搜索树高度平衡，因此我们每次递归都取升序序列的中间节点为根节点，这本质上就是二分查找的过程：

public static TreeNode sortedArrayToBST(int[] nums) {
        return dfs(nums, 0, nums.length - 1);
    }

    private static TreeNode dfs(int[] nums, int left, int right) {
        TreeNode root = null;
        if (nums == null || nums.length == 0)
            return null;
        if (left <= right) {
            int mid = left + ((right - left) >> 1);
            root = new TreeNode(nums[mid]);
            root.left = dfs(nums, left, mid - 1);
            root.right = dfs(nums, mid + 1, right);
        }
        return root;
    }

寻找两个正序数组的中位数

上面一题只是开胃菜，下面这题就加大难度了。LeetCode4.给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数 。算法的时间复杂度应该为 O(log (m+n)) 。

示例1：
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000 解释：合并数组 = [1,2,3] ，中位数 2
示例2：
输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000 解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

对于该题目，我们最直观的思路有两种：

• 使用归并排序合并这两个有序数组，得到一个大的有序数组，大的有序数组的中间元素的位置，即为中位数。该方法时间复杂度为O(m + n)，空间复杂度为O(m + n).
• 另一种方式是，我们可以不用合并两个数组，只要找到中位数的位置即可。我们先获取两数组的总元素的个数 len，然后获取中位数的位置，然后维护两个指针，初始化分别指向两个数组的下标00位置，每次将较小值后移一位(如果已到达数组末尾，则只需要移动另一个数组的指针)，直到到达中位数的位置。该方法可以将空间复杂度降为O(1),但是时间复杂度仍然是O(m+n).

要把时间复杂度降至O(log(m+n))，那我们大概率就要考虑二分、快排或者堆三个方面。而对于有序序列，通常要考虑是否能够使用二分来实现。
对于二分法，我们的核心问题就是依据什么规则将数据砍成一半。而本题是两个序列，所以我们的核心问题是如何从两个序列中分别砍半。图示如下：

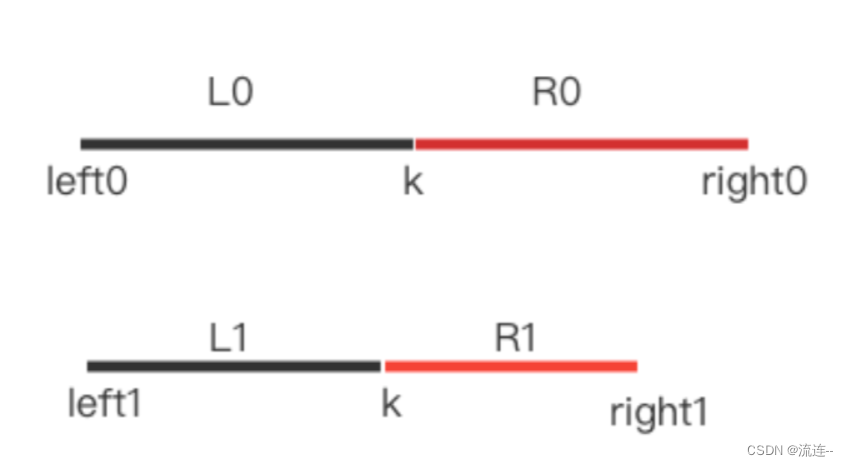
根据中位数的定义，当m+n 是奇数时，中位数是两个有序数组中的第(m+n)/2 个元素，当m+n 是偶数时，中位数是两个有序数组中的第(m+n)/2 个元素和第(m+n)/2+1 个元素的平均值。因此，这道题可以转化成寻找两个有序数组中的第 k 小的数，其中 k 为 (m+n)/2 或 (m+n)/2+1。
假设两个有序数组分别是LA 和LB。要找到第 k 个元素，我们可以比较LA[k/2−1] 和LB[k/2−1]。由于LA[k/2−1] 和LB[k/2−1] 的前面分别有LA[0…k/2−2] 和 LB[0…k/2−2]，即k/2−1 个元素，对于LA[k/2−1] 和LB[k/2−1] 中的较小值，最多只会有(k/2−1)+(k/2−1)≤k−2 个元素比它小，那么它就不能是第 k 小的数了。
因此我们可以归纳出以下几种情况：

• 如果LA[k/2−1]<LB[k/2−1]，则比LA[k/2−1] 小的数最多只有LA 的前k/2−1 个数和LB 的前k/2−1 个数，即比LA[k/2−1] 小的数最多只有k−2 个，因此LA[k/2−1] 不可能是第 k 个数，LA[0] 到LA[k/2−1] 也都不可能是第 k 个数，可以全部排除。
• 如果LA[k/2−1]>LB[k/2−1]，则可以排除LB[0] 到LB[k/2−1]。也就是一次砍掉一半。
• 如果LA[k/2−1]=LB[k/2−1]，则可以归入第一种情况处理。
  
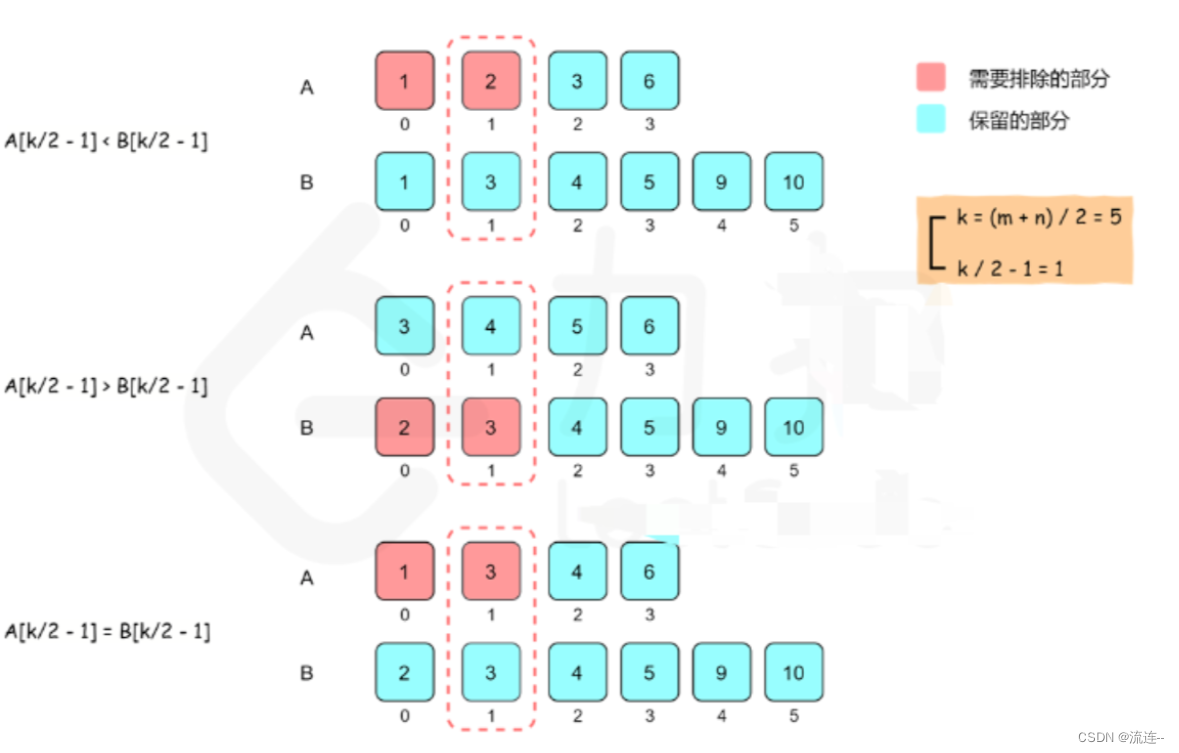
  可以看到，比较LA[k/2−1] 和LB[k/2−1] 之后，可以排除k/2 个不可能是第 k 小的数，查找范围缩小了一半。同时，我们将在排除后的新数组上继续进行二分查找，并且根据我们排除数的个数，减少 k 的值，这是因为我们排除的数都不大于第 k 小的数。
  以下边界情况需要特殊处理以下：
• 如果LA[k/2−1] 或者LB[k/2−1] 越界，那么我们可以选取对应数组中的最后一个元素。在这种情况下，我们必须根据排除数的个数减少 k 的值，而不能直接将 k 减去k/2。
• 如果k=1，我们只要返回两个数组首元素的最小值即可。
  实现代码(代码有点长，简单注释了一下)：

 public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int len1 = nums1.length,len2 = nums2.length;
        //获取两个数组的总长度
        int totalLength = len1 + len2;
        //若元素总数为奇数
        if ( totalLength % 2 == 1){
        	//获取其中位数下标
            int midIndex = totalLength/2;
            //k取midIndex + 1的原因是，中位数的位数k为其下标数加一
            double median = getKthElement(nums1,nums2,midIndex + 1);
            return median;
        } else {
         //若元素总数为偶数
         	//获取其目标中位数下标
            int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;
            double median = (getKthElement(nums1,nums2,midIndex1 + 1) + getKthElement(nums1,nums2,midIndex2 + 1)) * 0.5;
            return median;
        }
    }

    public static int getKthElement(int[] nums1, int[] nums2, int k) {
        int len1 = nums1.length, len2 = nums2.length;
        int index1 = 0, index2 = 0;
        while(true){
        	//当下标数index等于数组长度len,则该数组下标越界，则表示该数组所有元素已被砍去。
        	//直接获取另一数组剩余部分的k处即为所求。
            if (index1 == len1){
                return nums2[index2 + k - 1];
            }
            if (index2 == len2){
                return nums1[index1 + k - 1];
            }
            if (k == 1){
            //当k = 1时，两数组剩余部分的第一位的最小值为所求。
                return Math.min(nums1[index1], nums2[index2]);
            }
            int half = k/2;
            int newIndex1 = Math.min(index1 + half, len1) - 1;
            int newIndex2 = Math.min(index2 + half, len2) - 1;
            //对比两数组LA[k/2−1] 和LB[k/2−1]部分。
            //当LA[k/2−1]>=LB[k/2−1]时，则砍去LA[k/2-1]前面部分
            if (nums1[newIndex1] <= nums2[newIndex2]){
            	//k值则减去本次该数组砍去部分的元素个数
                k -= (newIndex1 - index1 + 1);
                //由于砍去LA[k/2-1]前面部分，下标取到newINdex1的下一位
                index1 = newIndex1 + 1;
            } else {
            //当LA[k/2−1]<LB[k/2−1]时，则砍去LB[k/2-1]前面部分
                k -= (newIndex2 - index2 + 1);//同上
                index2 = newIndex2 + 1;
            }
        }
    }