读文献时,有时求相关系数,有时求拟合优度,到底都是什么呢?
先给结论,
R
R
R与
R
2
R^2
R2没有关系,就如同标准差与标准误差没有关系一样。
1. 相关系数(R)
定义:变量之间线性相关的度量。分三种,spearman, pearson, kendall
公式:
ρ
=
C
o
v
(
X
,
Y
)
σ
X
σ
Y
\rho = \frac{Cov(X,Y)}{\sigma_X\sigma_Y}
ρ=σXσYCov(X,Y)
解释:自变量X和因变量Y的协方差/标准差的乘积。
- 协方差:两个变量变化是同方向的还是异方向的。X高Y也高,协方差就是正,相反,则是负。
- 为什么要除标准差:标准化。即消除了X和Y自身变化的影响,只讨论两者之间关系。
- 因此,相关系数是一种特殊的协方差。
2. 决定系数(R^2)
定义:对模型进行线性回归后,评价回归模型系数拟合优度。
公式:R2=SSR/SST=1-SSE/SST
SST (total sum of squares):总平方和
SSR (regression sum of squares):回归平方和
SSE (error sum of squares) :残差平方和。
解释:残差(residual):实际值与观察值之间的差异
在一组数据中,采用平均值做基线模型(图中黑线)
我们的模型(蓝线)都与这个黑线比较,来判断模型的好坏
var=sum(i-mean)^2
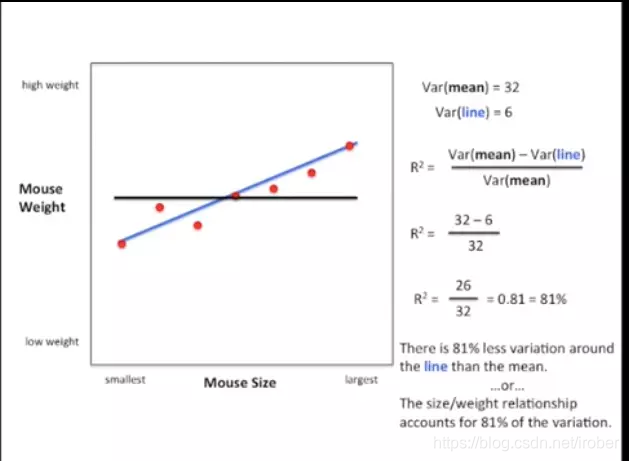
结论:R^2=81%,因变量Y的81%变化由我们的自变量X来解释。
R^2 的缺陷:当我们人为的向系统中添加过多的自变量,SSE会减少,从而R^2变大。因此我们采用校正R方,惩罚了过多无意义的自变量:





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








