Win32 OpenGL编程(6) 踏入3D世界
write by 九天雁翎(JTianLing) -- blog.csdn.net/vagrxie
提要
OpenGL本身就是为高性能3D图像处理而设计的,也多用于虚拟现实(VR),3D游戏等领域,本节正式开始接触3D领域,不再在2D的小世界中混了。(其实2D也是很大的领域了,当年不都是2D嘛?-_-!)本文主要以三角锥为例,从绘制一个3D坐标轴到绘制三角锥的线框模型到三角锥的实体模型,讲解在3D世界中我们绘制图形需要理解的事情,其实,单纯考虑3D图形还是很简单的,不就是多了一个Z坐标嘛。
3D坐标轴
不同一般的流程,我们从一个3D的坐标轴开始进入3D的世界,主要是为了将来与3D的线框模型做对比用的。
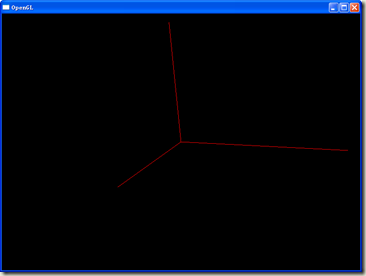
3D与以前学过的2D最大的不同就是我们需要考虑物体Z轴的坐标,而不再是假设任何物体的Z轴都是0.0,首先看我们绘制一个3D空间的坐标轴的情况,为了形象,我将其旋转了一定的角度。以下是源代码:
void DrawCoordinate()
{
static GLfloat fCoorDatas[] = { 0.0, 0.0, 0.0, // Origin
1.0, 0.0, 0.0, // X Dir
0.0, 1.0, 0.0, // Y Dir
0.0, 0.0, 1.0}; // Z Dir
static GLubyte ubyIndices[] = { 0, 1, // X Axis
0, 2, // Y Axis
0, 3}; // Z Axis
glEnableClientState(GL_VERTEX_ARRAY);
glVertexPointer(3, GL_FLOAT, 0, fCoorDatas);
glDrawElements(GL_LINES, 2, GL_UNSIGNED_BYTE, ubyIndices);
glDrawElements(GL_LINES, 2, GL_UNSIGNED_BYTE, ubyIndices+2);
glDrawElements(GL_LINES, 2, GL_UNSIGNED_BYTE, ubyIndices+4);
}
//这里进行所有的绘图工作
void SceneShow(GLvoid)
{
glClear(GL_COLOR_BUFFER_BIT); // 清空颜色缓冲区
glColor3f(1.0, 0.0, 0.0);
glPushMatrix();
glRotatef(30, 1.0, -1.0, 0.0);
DrawCoordinate();
glPopMatrix();
glFlush();
}
这样的3D坐标图中会看到Z轴实际上没有伸出窗口以外,而是被截断了,具体的原因在以后说视景体裁剪的时候会说明,但是现在可以理解为在OpenGL中,整个3D空间的Z轴也不是无限的,而是与窗口大小一样,形成一个3D的立方体空间,如同2D平面中超出窗口的部分会看不见,超出Z轴空间的部分也会看不见,此处的Z轴被截断就是如此。并且,我们可以通过源码定位的Z轴正方向(0.0, 0.0, 1.0)和图形中的现实看出来,在OpenGL的3D坐标系中,Z轴的正方向是指向屏幕外的,这点在XO3中讲过了,我们在这里通过坐标轴的图再次理解一下。理解了3D坐标系,那么所有的3D图形也就是如同2D图形一样的定坐标而已了。
三角锥(即四面体或金字塔形)线框模型
下面我们开始在上述3D坐标体系中绘制一个三角锥,这里还是先用线框模型来绘制。其实没有任何3D知识,仅仅靠凭空想象也能定下一个这样简单的三角锥的空间坐标,以下如是,其实没有什么技术难度,仅仅加入Z轴考虑,下列程序将三角锥不停的围绕其自身的Z轴自转,为了形象,同时绘制上面讲的三维立体坐标轴。格式有点混乱,是因为Live Writer的Code Snippet自动format不太好用-_-!完整源代码的排版是缩进较为对齐的。
void DrawWirePyramid(GLfloat adSize)为节省篇幅仅贴出关键片段,完整源代码见我博客源代码的2009-10-21/glWirePyramid 目录,获取方式见文章最后关于获取博客完整源代码的说明。
{
static GLfloat fPyramidDatas[] = { 0.0, 1.0, 0.0, // 三角锥上顶点
-1.0, 0.0, 1.0, // 底面左前顶点
1.0, 0.0, 1.0, // 底面右前下顶点
0.0, 0.0, -1.0}; // 底面后下顶点
GLfloat fPyramidSizeDatas[sizeof (fPyramidDatas)/sizeof (GLfloat)] = {0};
// 计算大小
for ( int i = 0; i < 12; ++i)
{
fPyramidSizeDatas[i] = fPyramidDatas[i] * adSize;
}
static GLubyte ubyIndices[] = { 0, 1, // 以下为三条侧边
0, 2,
0, 3,
1, 2, // 以下为三条底边
2, 3,
3, 1};
glEnableClientState(GL_VERTEX_ARRAY);
glVertexPointer(3, GL_FLOAT, 0, fPyramidSizeDatas);
for (int i = 0; i < 6; ++i)
{
glDrawElements(GL_LINES, 2, GL_UNSIGNED_BYTE, ubyIndices+i*2);
}
}
//这里进行所有的绘图工作
void SceneShow(GLvoid)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 0.0, 0.0);
glPushMatrix();
DrawCoordinate();
DrawWirePyramid(0.5);
glPopMatrix();
glRotatef(1.0, 0.0, 1.0, 0.0);
glFlush();
}
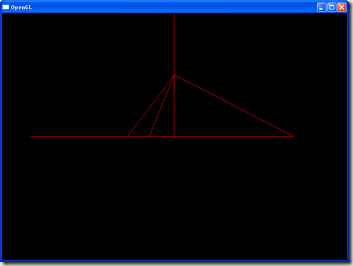
显示效果如下图所示。
三角锥
以上讲到3D图形都是以线框模型来演示的,主要是为了可以纯粹的考虑3D坐标的问题,下面我们开始加入颜色,看看真正的立体模型是怎么样的^^在上述例子中加入颜色实在再简单不过了,因为已经使用了顶点数组,我们只需要再启用一下颜色的数组就好了。
如下例所示:
void DrawSmoothColorPyramid(GLfloat adSize)
{
static GLfloat fPyramidDatas[] = { 0.0, 1.0, 0.0, // 三角锥上顶点
-1.0, 0.0, 1.0, // 底面左前顶点
1.0, 0.0, 1.0, // 底面右前下顶点
0.0, 0.0, -1.0}; // 底面后下顶点
GLfloat fPyramidSizeDatas[sizeof (fPyramidDatas)/sizeof (GLfloat)] = {0};
// 计算大小
for ( int i = 0; i < 12; ++i)
{
fPyramidSizeDatas[i] = fPyramidDatas[i] * adSize;
}
static GLfloat fPyramidColors[] = { 0.0, 0.0, 0.0,
1.0, 0.0, 0.0,
0.0, 1.0, 0.0,
0.0, 0.0, 1.0};
static GLubyte ubyIndices[] = { 0, 1, 2, // 正面
0, 1, 3, // 左侧面
0, 2, 3, // 右侧面
1, 2, 3}; // 底面
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);
glVertexPointer(3, GL_FLOAT, 0, fPyramidSizeDatas);
glColorPointer(3, GL_FLOAT, 0, fPyramidColors);
for (int i = 0; i < 4; ++i)
{
glDrawElements(GL_TRIANGLES, 3, GL_UNSIGNED_BYTE, ubyIndices+i*3);
}
}
//这里进行所有的绘图工作
void SceneShow(GLvoid)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 0.0, 0.0);
glPushMatrix();
DrawSmoothColorPyramid(0.5);
glPopMatrix();
glRotatef(1.0, 0.0, 1.0, 0.0);
glFlush();
}
为节省篇幅仅贴出关键片段,完整源代码见我博客源代码的2009-10-21/glSmoothColorPyramid/目录,获取方式见文章最后关于获取博客完整源代码的说明。
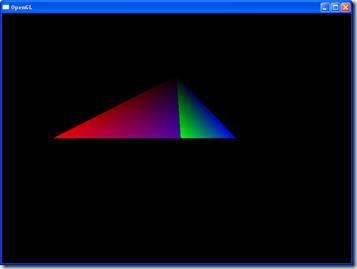
注意此例与上例中的区别,因为要显示完整的立体模型,就不能再用GL_LINES去画线了,我们需要使用GL_TRIANGLES来绘制三角形平面,一个三角锥其实不过就是一个四面体嘛。画上4个面,一切就OK。运行效果如下图:
小结
其实看完全文会发现,3D的世界也没有什么难的地方,无非就是多了一个Z轴需要考虑嘛,将整个屏幕想象成一个有前面空间,后面空间的立方体,然后想象出3D模型的坐标,一切也就简单了,本文主要讲的是三角锥,因为它是最简单的,大家可以试试立方体以增加难度,体会3D的坐标系统。
参考资料
1. 《OpenGL Reference Manual 》,OpenGL参考手册
2. 《OpenGL 编程指南》(《OpenGL Programming Guide 》),Dave Shreiner,Mason Woo,Jackie Neider,Tom Davis 著,徐波译,机械工业出版社
3. 《Nehe OpenGL Tutorials》,Nehe著,在http://nehe.gamedev.net/ 上可以找到教程及相关的代码下载,(有PDF版本教程下载)Nehe自己还做了一个面向对象的框架,作为演示程序来说,这样的框架非常合适。也有中文版 ,各取所需吧。
4. 《OpenGL入门学习》 ,eastcowboy著,这是我在网上找到的一个比较好的教程,较为完善,而且非常通俗。这是第一篇的地址:http://bbs.pfan.cn/post-184355.html
本系列下一篇《Win32 OpenGL编程(7) 3D视图变换——真3D的关键 》
本OpenGL系列其他文章
1. 《 Win32 OpenGL 编程(1)Win32下的OpenGL编程必须步骤 》
2. 《Win32 OpenGL编程(2) 寻找缺失的OpenGL函数 》
3. 《Win32 OpenGL编程(3) 基本图元(点,直线,多边形)的绘制 》
4. 《Win32 OpenGL编程(4) 2D图形基础(颜色及坐标体系进阶知识) 》
5. 《Win32 OpenGL编程(5)顶点数组详细介绍 》
完整源代码获取说明
由于篇幅限制,本文一般仅贴出代码的主要关心的部分,代码带工程(或者makefile)完整版(如果有的话)都能用Mercurial在Google Code中下载。文章以博文发表的日期分目录存放,请直接使用Mercurial克隆下库:
https://blog-sample-code.jtianling.googlecode.com/hg/
Mercurial使用方法见《分布式的,新一代版本控制系统Mercurial的介绍及简要入门 》
要是仅仅想浏览全部代码也可以直接到google code上去看,在下面的地址:
http://code.google.com/p/jtianling/source/browse?repo=blog-sample-code
原创文章作者保留版权 转载请注明原作者 并给出链接






















 1010
1010

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








