At a party N men throw their hats into the center of a room. The hats are mixed up and each man randomly selects one. Find the expected number of men who select their own hats.
译: N 个人把自己的帽子扔进了一个房间,他们的帽子全部混在了一起,然后每个人再随机地取回一顶帽子,请问恰好找到自己帽子的人数的期望。

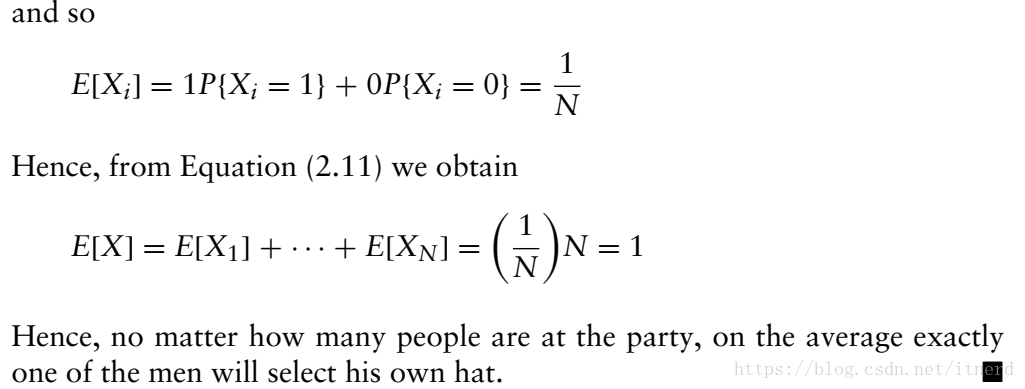
结果很震惊!无论有多少人扔出自己的帽子,平均来看,总有1人能捡回自己的帽子!
Show that Var(X) = 1 when X is the number of men who select their own hats
译: 证明找回自己帽子的人数的方差等于1。
solution:


想不到吧!
X
i
,
X
j
X_i, X_j
Xi,Xj的协方差不是 0 哦!!!
Suppose that those choosing their own hats depart, while the others (those without a match) put their selected hats in the center of the room, mix them up, and then reselect. Also, suppose that this process continues until each individual has his own hat.
(a) Find
E
[
R
n
]
E[R_n]
E[Rn] where
R
n
R_n
Rn is the number of rounds that are necessary when n individuals are initially present.
(b) Find
E
[
S
n
]
E[S_n]
E[Sn] where
S
n
S_n
Sn is the total number of selections made by the n individuals,
n
≥
2
n\geq2
n≥2.
(c) Find the expected number of false selections made by one of the n people,
n
≥
2
n\geq2
n≥2.
译: 假设找到自己帽子的人就离开了,剩下的人把帽子丢回,混合均匀,开始新一轮捡帽子。直到所有人找回自己最初的帽子。
问:如果开始时有 n 个智障来丢帽子,
(a) 平均需要捡多少轮才能结束?
(b) 捡帽子的总次数的期望是多少?按一人一轮1次计。
n
≥
2
n\geq2
n≥2。
(c) 每个人错捡帽子次数的期望是多少?
n
≥
2
n\geq2
n≥2.




























 527
527

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










