数据结构与算法笔记——树(Tree)

 什么是树

树的一些概念

根节点、叶子节点、父节点、子节点、兄弟节点，还有节点的高度、深度以及层数，树的高度。

你有没有发现, "树"这种数据结构真的很像我们现实生活中的"树" ,这里面每个元素我们叫作"节点" ;用来连线相邻节点之间的关系,我们叫作"父子关系"。

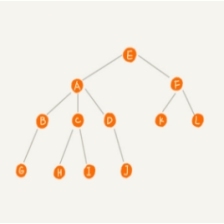
比如下面这幅图, A节点就是B节点的父节点, B节点是A节点的子节点。 B.C、D这三个节点的父节点是同一个节点,所以它们之间互称为兄弟节点。我们把没有父节点的节点叫作根节点,也就是图中的节点E,我们把没有子节点的节点叫作叶子节点或者叶节点,比如图中的G、H、1、J、叶子书。

                                      

节点的高度 = 叶子节点到节点的最长路径(边数，从下到上)

节点的深度 = 根节点到这个节点所经历的边的个数（从上到下）

节点的层数 = 节点的深度+1

树的高度 = 根节点的高度

                 

层数:数节点,高度从下往上数变数,深度从上往下数变数

二叉树(Binary Tree)

什么是二叉树:

每个节点最多有两个"叉" ,也就是两个子节点,分别是左子节点和右子节点。

         

编号2 的二叉树中,叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个于节点,这种二叉树就叫作满二叉树。

编号3 的二叉树中,叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后层,其他层的节点个数都要达到最大,这种二叉树叫作完全二叉树。

 

二叉树的遍历:

• 前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。自左右
• 中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。左自右
• 后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。左右自

                     

 

二叉查找树

什么是二叉查找树:

二叉查找树是二叉树中最常用的一种类型,也叫二叉搜索树。顾名思义,二叉查找树是为了实现快速查找而生的。不过,它不仅仅支持快速查找一个数据,还支持快速插入、删除一个数据。

二又查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。

                         

平衡二叉查找树

什么是平衡二叉查找树:

二叉树中任意一个节点的左右子树的高度相差不能大于1。

                       

常见的平衡二叉查找树:

Splay Tree (伸展树) 、Treap (树堆)等,但是我们提到平衡二叉查找树,听到的基本都是红黑树。

红黑树

红黑树的英文是"Red-Black Tree" ,简称R-B Tree。它是一种不严格的平衡二叉查找树

红黑树的特点:

• 根节点是黑色的;
• 每个叶子节点都是黑色的空节点(NIL) ,也就是说,叶子节点不存储数据;
• 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
• 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;