[数据结构]单调栈与单调队列

可能会用到的前置知识：
栈与栈的应用
队列与队列的应用

---

有时候题目中可能会出现一些需要维护单调性的内容，例如最典型的滑动窗口最值问题等。又或者需要通过几维不同的单调性同时维护，那么这时单调队列可能会很有用处，将原有的高级数据结构需用$O(n\log n)$的时间复杂度才能解决的问题简化到用较为容易写的单调队列在$O(n)$时间复杂度内完成。

有时在一些序列问题上，我们需要做的是维护原序列中某个单调递减的子序列，或者查找右侧的第一个较大值，在这样的类似问题里，我们可以考虑使用单调栈来解题，也会比树状数组等高级数据结构更快更简便。

单调栈

我们考虑以下的问题：

给定一个长度为n的序列A[1…n]，从左到右排成一排，现在要求你求出：
每个元素右侧的位置最靠近的比它大的数。（称为右邻数）

解释一下题意，其实就是找序列中某个位置右侧且最接近的一个值，使得这个值比原位置的值要大。（相似题意可看Luogu 1901 发射站，意思大致相同，只不过这里只需要考虑右侧）

考虑一个简化版本：假如我们现在已经得到了一个单调递减的序列，在右侧出现了一个新的值，这个值比单调递减段的最后一个值要大，那么在原来的单调递减序列中肯定会有一个后缀的右邻数等于这个新的值。举一个简单的例子：
原来的单调递减序列A=[6,5,3,2,1]，新加入的值为4，那么A[3…5]即3,2,1的右邻数就是4了。
这是显然的，而且我们可以求出这个后缀，将新加入的值与单调递减序列从最右侧开始的数逐个比较，假如新数比原来数小，那么就可以接在这个单调递减序列的后面——它不会比原来序列里的任何数大。否则就将原来序列里的最后一个数的右邻数定义为新数，然后再考虑单调递减序列的第二大数…

依然用这个例子，单调递减序列A=[6,5,3,2,1]，新数为4，首先4与1作比较，发现4比1要大，那么1的右邻数为4，将1从单调递减序列中去除；
接着来看2，用4与2作比较，发现4比2大，那么2的右邻数为4，将2从单调递减序列中去除；
然后看3，用4与3作比较，发现4比3大，那么3的右邻数为4，将3从单调递减序列中去除；
最后看5，用4与5作比较，发现4比5小，那么4直接接在单调递减序列的末尾，此时A=[6,5,4]。

看到这里，你可能已经意识到，简化版的问题和原问题是等价的，因为一个单调递减序列在加入一个数后依然能够通过上述方法维护成一个新的单调递减序列，因此这个序列可以保证始终单调递减。由于对于这个序列的操作都在同一端（右端）进行，所以可以用栈来实现，因此这种算法就称为单调栈算法。

上面只提供了一个大致思路，如果还不明白的话，可以看代码理解：

#include <bits/stdc++.h>
using namespace std;
const int MAXN=1000010;
int p[MAXN],a[MAXN],h[MAXN],ans[MAXN],n,cur;  //维护了一个栈，但用两个数组a和p
int main () {
    scanf("%d",&n);
    for (int i=1;i<=n;i++) {
        scanf("%d",&h[i]);
    }
    for (int i=1;i<=n;i++) {
        while (cur!=0&&h[i]>a[cur]) {  //当新数比单调递减序列的末尾大时要删除
            ans[p[cur--]]=i;    //原来序列的末尾的右邻数等于当前位置
        }
        a[++cur]=h[i];    //a数组用来记录栈中元素的值
        p[cur]=i;    //p数组用来记录栈中元素在原数组的下标
    }
    for (int i=1;i<=n;i++) {
       printf("%d ",ans[i]);    //注意这里输出的是右邻数的下标
    }
    return 0;
}

由于每个数会进栈出栈最多一次，所以时间复杂度为$O(n)$。
这里想明白了，上面那道发射站的题目就很简单了。
下面来看另外一道单调栈的题目：
POJ 2559 Largest Rectangle in a Histogram
乍一看可能还没有什么思路，但是如果将这样的一些矩形问题转化成一个序列问题，就有可能会豁然开朗，我们将题目换一种方式理解：
给定一个长度为n的序列A，找出其中的一个子段A[l…r]，使得段的长度与段中最小值的乘积最大，求出这个乘积。

方法1：暴力，时间复杂度为$O(n^3)$

枚举l和r，并暴力计算最小值，最后求出所有答案中的最大值，肯定会超时。

方法2：暴力+最小值优化，时间复杂度为$O(n^2)$

在暴力的基础上，使用线段树或者ST表等方法来优化求最小值的方法，最终可以降低一个n的复杂度，但是依然是会超时的。

方法3：单调栈，时间复杂度为$O(n)$

我们的问题是找到一组合适的l和r，使得下式最大化：
$(r-l+1)\ast \underset{l\le i\le r}{\min }A[i]$

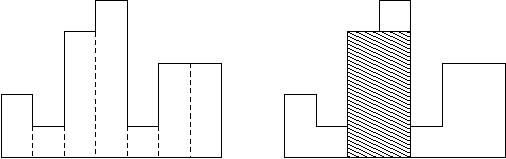
我们以题目中的样例为例，A=[2,1,4,5,1,3,3]，用单调栈的思想。如果已经有一个单调递增序列，突然来了一个较小的数，例如一开始的单调递增序列B=[2]，于是下一个是更小的1，那么我们这个时候考虑矩形包含第一列的A[1]=2时的情况。
第一列的2如果要选到顶，那么就无法向右扩展了，这是因为它的右边就是一个更小的1，没有它高，所以无论如何是不可能跨过1到达下一个数的，所以包含2的矩形面积最大为2，在单调递增序列中删除，换成较小的1（这是因为2中比1大的部分已经无效），此时单调递增序列为[1,1]。
接着来了4和5，和1一起构成单调递增序列[1,1,4,5]，于是来了一个较小的1，1比单调递增序列的末尾5要小，因此以5为顶的矩形不能向右继续扩展，面积为$5\times 1=5$，将5从单调递增序列中删除，换成1（因为5中比1大的部分已经无效），变为[1,1,4,1]。
继续考虑序列末尾4，依然比1大，所以以4位顶的矩形只能跨越到5而不能继续，因此以4为顶的矩形面积最大为$4\times 2=8$，将4删除，换成1，变为[1,1,1,1]，此时可以插入新的1，变为[1,1,1,1,1]。
依次类推，这是一个单调栈。最终单调栈中可能还剩下若干元素，所以我们可以最简单地在序列最后加上一个数0，这样在最后就会强制将所有剩余元素压出了。
大致思路就是如此，具体实现可以参考题目解析。

单调队列

以一道例题引出：
POJ 2823 Sliding Window 或 Luogu 1886 滑动窗口

给出一个长度为n的序列，求出长度为k的每个子段的最大值以及最小值

方法1：暴力，时间复杂度为$O(n^2)$

强行枚举每个滑动窗口中的数，求出最大值和最小值，超时。

方法2：数据结构优化，时间复杂度为$O(n\log n)$

利用线段树或ST表来优化最大值/最小值的求解，可以达到较低复杂度，但还不是最快的，在极端数据下可能会被卡。

方法3：单调队列，时间复杂度为$O(n)$

以求最大值为例，分析题目中的一个重要性质：
若$i<j$，且$a[i]<a[j]$时，计算到j之后时，i就永远不会成为答案。这是因为j的值更大，而且由于j本身也更大，所以i离开窗口会更早，也就是j存在的时间会更长，综上两方面的考虑，j出现后i就没有了意义。

因此我们建立一个元素单调递增的队列。我们先将第一个元素加入队列，然后依次考虑每一个元素：
如果队头的元素已经超出了窗口范围，则删除队头；
如果新元素比队尾元素大，则根据之前的总结规律，将队尾出队，再与新的队尾进行检验；
最后将新元素加入队尾。
此时队头的元素就是当前滑动窗口的最大值。

单调队列是双端队列。

我们来说明它的单调性，因为每次加入元素时都会检验与队尾的大小关系，只有当其小于队尾时才会加入，所以一定可以保证值从队头至队尾单调递减，因此队头的元素就是最大值。
此外，由于队列先进先出的性质，所以下标小的元素先进入队列，也更加靠前，因此实际上队列中元素的下标是从队头至队尾单调递增的，即队头的元素的下标最小，所以只要队头的元素在窗口内，所有元素就都在窗口之内。

综上，这种算法是正确的。
以下代码中，b[0]存的是值，从队头至队尾单调递减，b[1]存的是下标，从队头至队尾单调递增，cur1为队头，cur2为队尾。

#include <bits/stdc++.h>
using namespace std;
const int MAXN=1000010;
int n,k,a[MAXN],b[2][MAXN],cur1=1,cur2=1;    //cur1--head, cur2--tail
int main () {
	scanf("%d%d",&n,&k);
	for (int i=1;i<=n;i++) {
		scanf("%d",&a[i]);
	}
	for (int i=1;i<=n;i++) {
		while (cur2>=cur1&&i-b[1][cur1]>=k) {    //cur2>=cur1表示队列不空
			cur1++;    //这里检验队头是否还在窗口内
		}
		while (cur2>=cur1&&b[0][cur2]>=a[i]) {    //窗口最小值
		//while (cur2>=cur1&&b[0][cur2]<=a[i]) {    窗口最大值 
			cur2--;    //这里检验值的单调性
		}
		b[0][++cur2]=a[i],b[1][cur2]=i;
		if (i>=k) {
			printf("%d ",b[0][cur1]);
		}
	}
	return 0;
}

单调队列还能解决其他一些问题，例如：
Luogu 2564 [SCOI2009]生日礼物
题目大意：给定直线上n个点的位置和种类，选择一个最短的区间使得区间内包含每一种点。

首先将每种点的最靠左的点按从左到右放进队列，此时显然一个备选答案就是队头与队尾的位置差。
另外，我们考虑在右端点确定的情况下决定最优的左端点位置（其实就是要尽量靠右），保证每种彩珠都有出现，因此我们可以开变量cnt[i]表示第i种彩珠目前在区间出现了多少次。
如果队首元素（坐标最小）出现的次数大于1，则可以删去，这是因为删去后依然有这种彩珠存在，如果出现的次数恰好等于1，则不能删去，因为删去后这种彩珠就不再出现再队列中。
因此只要维护cnt数组，并在枚举时将当前彩珠加入队列，检查队首是否可以删去，即可解决问题。

单调队列常用来优化动态规划算法。近年来在noip中也有考到，与其他算法综合，难度较大：
NOIP 2017 普及T4 跳房子，综合了二分答案+动态规划+单调队列优化的算法，是一道比较综合的题目。