数据结构之二叉搜索树的增删查改（图解，代码6000多字总结）

最新推荐文章于 2024-02-29 20:32:41 发布
最新推荐文章于 2024-02-29 20:32:41 发布
阅读量638 收藏 2
点赞数 1
分类专栏： 数据结构 文章标签： 二叉树 数据结构 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/javadocdoc/article/details/119706451
版权

文章目录

一：概念

1.使用场景

 二叉搜索树既可以作为一个字典又可以作为一个优先队列

2.定义

  • 二叉搜索树是一颗符合如下性质的二叉树：
    - 任何节点，左子树中的任何一个关键字都不大于该节点，右子树中的任何一个关键字都不小于该节点
  • 可以用链表来表示，其中的每一个节点都是一个对象，节点属性包括key，left，right，parent，卫星数据（key的一些附属信息）。
  • 如果对应的节点不存在的时候，则相应属性的值为nil。
  • 根节点是整棵树中唯一一个父指针为nil的节点
class TreeNode{
	// 该节点存储的关键字
	object key
	// 左节点
	TreeNode left;
	// 右节点
	TreeNode right;
	// 父节点
	TreeNode parent;
}

3. 示例

对于任何节点，左子树中的任何一个关键字都不大于该节点，右子树中的任何一个关键字都不小于该节点
在这里插入图片描述
如上图所示，整个树的root的关键字是6，root的左子树中包含的关键字2,5,5，他们均不大于6。而在右子树种的关键字7和8，他们均不小于6.

鉴于二叉搜索树左<中<右的特点，所以一般我们使用中序遍历，这样遍历的结果就天然的是升序

4.遍历

INORDER-TREE-WALK(x)
if x!=NIL
	INORDER-TREE-WALK(x.left)
	print x.key
	INORDER-TREE-WALK(x.right)

时间复杂度：O(n)

4.1 前驱和后继

 在中序遍历下，前驱指的是前一个节点，后继指的是后一个节点
 如果遍历之后的顺序是dxsf，那么d是x是前驱，s是x的后继

5.基本操作

5.1 查找

查找指在一个二叉搜索树中查找一个具有给定关键字的节点，如果存在返回节点，如果不存在返回nil。

// 参数x指的是查找的当前节点。参数k指的是查找的目标关键字
TREE-SEARCH(x,k）
// 当x为nil的时候，那么k必然不存在，所以返回nil即x就好；
// 当x节点存储的关键字刚好是目标关键字的时候，那么返回x
	if x==NIL or k==x.key
		return x
// 当目标关键小于当前节点存储的key的时候，就去x节点的左子树中查找。因为二叉搜索树的特点就是右子树存储的关键字均大于当前节点的关键字，所以在这种情况下可以直接忽略右子树
	if k<x.key
		return TREE-SEARCH(x.left,k)
// 当目标关键不小于当前节点存储的key的时候，就去x节点的右子树中查找，因为二叉搜索树的特点就是右子树存储的关键字均大于当前节点的关键字。
	else
		return TREE-SEARCH(x.right,k)

假设二叉搜索树的高度是h，那么根据上面的伪代码可以知道整个递归次数应该是<=h的，所以时间复杂度为O(h)

这里还有一种非递归写法

TREE-SEARCH(x,k）
	y=x.key
	while x!=NIL and k!=y
		if k<x.key
			x=x.left
		else
			x=x.right
	
	return x

5.2 最小关键字

TREE-MININUM(x)
	while x.left!=NIL
		x=x.left
	return x

因为二叉搜索树的规则是左子树小于节点小于右子树，所以从上至下，遍历到左节点为nil的时候即为存储最小关键值的节点

5.3 最大关键字

TREE-MININUM(x)
	while x.right!=NIL
		x=x.right
	return x

因为二叉搜索树的规则是左子树小于节点小于右子树，所以从上至下，遍历到右节点为nil的时候即为存储最大关键值的节点

5.4 插入

插入操作是会导致搜索二叉树的动态集合发生变化，所以在修改数据结构的时候需要注意，要保持二叉树性质的成立

工作流程： 从根节点出发，通过对每一个节点存储关键字和目标关键字的比较来确定路径的走向

// 在树T中插入节点z
TREE-INSERT(T, z)
// 创建一个临时节点，用来存储while循环结束的叶子节点
	y=nil
	// 从根节点开始
	x=T.root
	// 从上至下，直到遇到叶子节点
	while x!=NIL
		y=x
		//如果插入节点小于当前节点，那么就往左子树上去寻找位置
		if z.key<x.key
			x=x.left
		//如果插入节点大于当前节点，那么就往左子树上去寻找位置
		else
			x=x.right
	
	// 将插入节点的父亲设置为叶子节点y
	z.p=y
	//如果y==nil，那就说明没有进入while循环，即T.root是nil,所以直接将该节点设置为root
	if y==nil
		T.root=z
	// 判断要将插入节点作为叶子节点的左子树还是右子树
	else if y.key<z.key
		y.left=z
	else
		y.right=z

从上述伪代码中可以看到，消耗时间的大头在于while循环，从上至下的查找路径，可知时间复杂度为O(h)

从上面的分析中可以看到，插入的节点都是被放在叶子节点的子节点，可以对于整棵树的上层部分是没有影响的

5.5 删除

删除操作与上面的操作不同，而且比较复杂，是因为当删除一个内部节点（非叶子节点）的时候，需要调整整棵树，在调整的时候也需要注意满足搜索二叉树的性质

首先我们需要考虑如下几种情况：
假设现在要从树T种删除节点z

5.5.1 z没有子节点

那么只需要删除叶子节点z，并将z的父节点的子节点设置为nil就好
在这里插入图片描述

5.5.2 z只有一个右子节点

那么只需要删除叶子节点，并用z的子节点来代替z的位置

在这里插入图片描述

5.5.3 z只有一个左子节点

那么只需要删除叶子节点，并用z的子节点来代替z的位置
在这里插入图片描述

5.5.4 z有两个子节点的时候

我们需要去寻找z的后继y来根据情况分析

4.1. 如果z的后继y是z的右子节点的话，那么y的左子树必然是nil。因为当y的左子树不是nil的时候，那么在中序遍历下，遍历z之后，必然会遍历y的左子树，然后再到y，也就是下面介绍的4.2那种情况。

删除z节点，将z节点左节点设置为y的左节点
在这里插入图片描述
4.2 z的后继y不是z的右子节点的话，
如图介绍，节点r表示一颗高度为h1的子树，那么z的后继y就是z的右子树中最左路径的终点，也可以理解为右子树中的最小节点，即y的左子树是nil

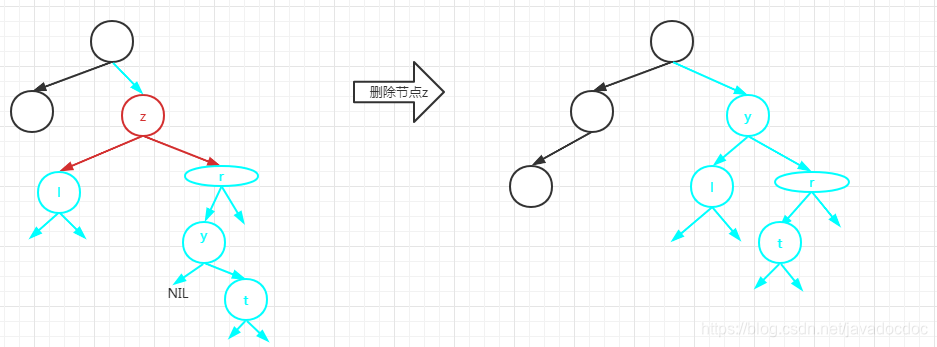
在这里插入图片描述

在删除节点z有两个子节点的时候，树调整的原则就是使用后继节点y替换删除节点（因为后继节点是删除节点的右子树中最小的节点，所以用这个节点来进行替换，才不会破坏搜索二叉树左<中<右的性质）。面对4.2的情况，因为后继节点y没有左子节点，所以可以用将删除节点z的左子节点l作为y的左子节点。那么这个时候就会两个被破坏的右子节点，一个是删除节点z的右子节点r，另外一个是后继节点y的右子节点t。
那么现在的问题就是节点r和节点y和节点t之间的关系。
为了不违反搜索二叉树的性质，我们先来看一下他们的大小关系
y<t<r
然后考虑t和r只能在y的右子树上
所以有如下几种情况
在这里插入图片描述

可以看到，这两种情况都是符合条件的，区别的t和r的层级关系。第一种情况，因为t节点下面还有子树，如果我们把r节点作为t的子子节点的话，必然要多遍历几层，而且也更改了叶子节点，所以用第二种方式相对来说节点移动简单而且对叶子节点的修改比较少

对于删除节点，可能的树调整方案上面已经分析过，那么接下来就看一下伪代码

首先看到，不管是哪种情况，都会有节点y来替换节点z的这一步，那么先实现一个这样的功能

这个方法实现的是更换节点和父节点的一种关系置换，不修改子节点的关系

// 将二叉搜索树T上面的u节点替换为v节点
TRANSPLANT(T,u,v)
// 当u.p==Nil的时候，那就说明u是root，那么就直接设置root为v就可以
	if u.p==NIL
		T.root=v
	// 如果u是左子节点的话，那么就设置父节点的左子节点为v
	else if u.p.left=u
		u.p.left=v
	// 如果u是右子节点的话，那么就设置父节点的右子节点为v
	else
		u.p.right=v
	// 设置新节点的父节点
	if v!=NIL
		v.p=u.p

节点的删除过程

// 从二叉搜索树T中删除节点z
TREE-DELETE(T,z)
// z的左子节点为nil的情况，直接用右子节点替换z就可以
	if z.left==Nil
		TRANSPLANT(T,z,z.right)
	// z的左子节点不为nil，右子节点为nil的情况，直接用左子节点替换z就可以
	else if z.right==Nil
		TRANSPLANT(T,z,z.left)
	// z的左右子节点都不为nil的情况
	else
		// 找到z的后继，即右子树的最小值,那么就可以确认y的左子节点是nil
		y=TREE-MININUM(T,z.right)
		// 第4.1种情况，即后继是z的右子节点的情况:
		if y.p==z
			//使用y来替换z
			TRANSPLANT(T,z,y)
			// 将z的左子节点设置y的左子节点
			y.left=z.left
			z.left.p=y
		// 第4.2种情况，即后继不是z的右子节点的情况:
		else
			// 其实在4.2情况下，我们需要调整的节点关系有两个，一个是z的左子节点和y的关系；一个是z的右子节点和y的右子节点的关系
			TRANSPLANT(T,y,y.right)
			y.right=z.right
			y.right.p=y
			TRANSPLANT(T,z,y)
			y.left=z.left
			z.left.p=y

可以看到上面的代码有一部分还是重复调用的，所以我们可以调整一下

TREE-DELETE_v2(T,z)
	if z.left==Nil
		TRANSPLANT(T,z,z.right)
	else if z.right==Nil
		TRANSPLANT(T,z,z.left)
	else
		y=TREE-MININUM(T,z.right)
		if y.p!=z
			TRANSPLANT(T,y,y.right)
			y.right=z.right
			y.right.p=y
		TRANSPLANT(T,z,y)
		y.left=z.left
		z.left.p=y

时间复杂度：从上面的代码中可以看出，时间的消耗在两个地方TRANSPLANT和TREE-MININUM，但是TRANSPLANT这里只涉及到两个节点之间关系指针的变化，所以使用的是常数时间。TREE-MININUM这里需要根据指定节点从上至下寻找最小关键值，和树的高度h有关，所以时间复杂度为O(h)

安勿期
关注
  • 1
    点赞
  • 踩
  • 2
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
实现二叉树的增删改查基本操作的c++程序
05-09
很好很强大的程序，实现二叉树的增删改查等基本操作，操作简单，程序结构清晰
数据结构之树
xiaotai1234的博客
10-17 404
数据结构之树 一、二叉树 1.为什么需要树这种数据结构 2.树的常用术语 3.二叉树的概念 二、二叉树遍历 1.前中后序遍历 2.二叉树查找节点 3.二叉树删除节点 package com.atguigu.tree; public class BinaryTreeDemo { public static void main(String[] args) { //先需要创建一颗二叉树 BinaryTree binaryTree = new BinaryTree(); //创
二叉树的增删查改
最新发布
strive_mianyang的博客
02-29 677
本节复习二叉树的增删查改， 二叉树的知识相对于前面的循序表， 链表， 以及栈和队列都要多一些。同时二叉树的增删查改理解起来相对来说要困难一些。本节来好好复习一下二叉树的增删查改。
二叉树（链表实现）--增、删、改、查
一名小白的博客
07-25 649
二叉树（链表实现） 1.1 树的基本定义 ​ 树是我们计算机中非常重要的一种数据结构，同时使用树这种数据结构，可以描述现实生活中的很多事物，例如家谱、单位的组织架构、等等。 ​ 树是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。 树具有以下特点： 每个结点有零个或多个子结点； 没有父结点的结点为根结点； 每一个非根结点只有一个父结点； 每个结点及其后代结点整体上可以看做是一棵树，称为当前结点的父结点的一个子树；
001数据结构之树增删改查介绍
热爱编写程序的药学在读书
11-03 563
这篇文章讲解关于树的一系列知识，后续可能会根据知识点的数量分开写成多个文章，你可以从中获取如下知识： 对之前已有的存储方式回顾 对树有个简单的了解 问题引入：为什么需要树这种结构呢？ 一、已知的存储方式回顾 1、数组的优点与缺点 可以方便查找，排序等 当他数据满之后，当要插入数据的，都会降低效率。 比如我们的ArrayList这个类，它也是按一定的比例来扩容。 2、链表的优点与缺点 链表摒弃了数组的浪费内存，但是它仍然存在检索比较浪费时间的。 3、需要原因 能提高数据存储，读取得效率，比如利
二叉树及其应用（增删改查）
weixin_48102054的博客
09-16 853
二叉树及其应用（增删改查）
数据结构--------二叉树的增删查改
qq_37807989的博客
06-25 362
public class Node { public Node right; public Node left; public int data; public Node(int data) { this.data = data; } public Node() { } } /** * 二叉树方法: * ...
二叉树的增删改查
weixin_44135991的博客
05-04 558
首先建立Node public class Node<T extends Comparable<T>> { private T date; private int index; private Node<T> lchile; private Node<T> rchile; public Node(){ } p...
详解二叉搜索树的增删改查
qq_52906742的博客
08-15 789
二叉查找树（英语：Binary Search Tree），也称为二叉搜索树、有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、多重集、关联数组等。2.1 搜索树的节点二叉搜索树节点通常采用的是二叉链结构，就是一个指针指向左孩子一个指针指向右孩子。 2.2 构建树的结构 三、二叉搜索
javascript数据结构之二叉搜索树实现方法
10-23
主要介绍了javascript数据结构之二叉搜索树实现方法,较为详细的分析了二叉搜索树的概念、原理与JavaScript实现二叉搜索树的方法,对于学习JavaScript数据结构具有一定参考借鉴价值,需要的朋友可以参考下
陈越、何钦铭-数据结构作业12：是否同一棵二叉搜索树
04-20
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。于是对于输入的...
BST.rar_bst_二叉搜索树_数据结构动画_树 动画
09-23
数据结构中的二叉搜索树，对于插入和遍历的功能，有动画显示
python 版本的树的增删查改
08-14
用python 写成的树结构的增删查改，便于以后调用
二叉树增删改查java_java--二叉树增删改查详解
weixin_29064009的博客
02-27 374
二叉树的删除和修改二叉树的删除比较复杂。你要先找到要删除的结点。要删除的结点对象并不一定要删除。因为通过函数调用得到的只是他的副本。并不会真正的把他删掉。你只要让他不在树上就ok了。让删除结点的父节点，左右孩子结点用新的结点来指向就把该结点从树上删除了。然后找到要插入的结点。找法有三种情况：删除结点有左孩子这种情况下，找到左孩子的最右孩子。找到的结点是要上去的结点。如果该左孩子没有右孩子，则该左孩...
使用zTree实现对树结构的增删改查
小鹏要逆袭的博客
01-09 1310
一、目标 想要实现的效果如下： 二、数据如何设计 使用集成的方式来进行树结构的设计，具体数据库表设计如下： 组织表： 字段名称 数据类型 描述 id integer 主键 orgname string 组织名称 pid integer 父节点的编号 三、基于pid的数据库设计，ztree的使用 这里需要用到ztree这...
树的增删改查
Mr.田的博客
11-07 901
package Tree; import java.util.Stack; //定义树节点 class TreeNode{ int val; TreeNode left; TreeNode right; TreeNode(int x){ val=x; } } //我想要跟链表一样实现一个树的增删改查 //1.建立一个二叉树TreeBuild(); //2.增 add(TreeNode root); //3.删delete(TreeNode root
搜索二叉树的增删改查
蓝胖子的博客
10-03 177
唯一的难点就是当当前节点就是要删除的那个节点时该怎么处理的问题。还有一种方式，当当前节点就是待删除的节点且左右子树都存在时，任命当前这个节点右子树中最小的那个节点为根节点，这个新的根节点的左子树就是原来根节点的左子树，这个新节点的右子树是原来根节点的右子树删除这个新节点之后的右子树（注意要求先求新节点的右子树在求新节点的左子树）当前节点就是要删除的那个节点时而且我左右子树都在的时候是最难想的，其实只需要把原来的头节点的右子树上的最小值（最左边那个）的左子树改成原来头节点的左子树即可。
二叉搜索树相关操作，添加、删除、修改元素等
weixin_50901244的博客
03-14 1436
二叉搜索树笔记整理1.概念2.二叉搜索树相关操作2.1 二叉搜索树的插入和查找2.1 查找二叉搜索树的最小值和最大值2.2 二叉搜索树的删除和修改2.2.1 二叉搜索树最小最大值删除2.2.1 二叉搜索树删除任意指定值 1.概念 二叉搜索树又称二叉排序树，它或者是一棵空树**，或者是具有以下性质的二叉树: 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值 它的左右子树也分别为二叉搜索树 二分搜索树一般不考虑元素相等的情况（元素不重复）
「leetcode」450. 删除二叉搜索树中的节点：【递归】【迭代】详解
代码随想录
10-23 531
二叉搜索树删除节点就涉及到结构调整了
c++二叉查找树增删查改
11-11
以下是C++实现二叉搜索树的增删查改的示例代码： 1. 结点类的实现： ```c++ class Node { public: int val; Node* left; Node* right; Node(int val) { this->val = val; this->left = nullptr; this->right = nullptr; } }; ``` 2. 二叉搜索树类的实现： ```c++ class BST { public: Node* root; BST() { root = nullptr; } // 插入操作 void insert(int val) { root = insertNode(root, val); } // 删除操作 void remove(int val) { root = removeNode(root, val); } // 查找操作 bool search(int val) { return searchNode(root, val); } // 修改操作 void modify(int oldVal, int newVal) { remove(oldVal); insert(newVal); } private: // 插入结点 Node* insertNode(Node* node, int val) { if (node == nullptr) { return new Node(val); } if (val < node->val) { node->left = insertNode(node->left, val); } else if (val > node->val) { node->right = insertNode(node->right, val); } return node; } // 删除结点 Node* removeNode(Node* node, int val) { if (node == nullptr) { return nullptr; } if (val < node->val) { node->left = removeNode(node->left, val); } else if (val > node->val) { node->right = removeNode(node->right, val); } else { if (node->left == nullptr && node->right == nullptr) { delete node; node = nullptr; } else if (node->left == nullptr) { Node* temp = node; node = node->right; delete temp; } else if (node->right == nullptr) { Node* temp = node; node = node->left; delete temp; } else { Node* temp = findMin(node->right); node->val = temp->val; node->right = removeNode(node->right, temp->val); } } return node; } // 查找结点 bool searchNode(Node* node, int val) { if (node == nullptr) { return false; } if (val == node->val) { return true; } else if (val < node->val) { return searchNode(node->left, val); } else { return searchNode(node->right, val); } } // 查找最小值 Node* findMin(Node* node) { while (node->left != nullptr) { node = node->left; } return node; } }; ```

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值